【你也能看得懂的电磁场与电磁波系列连载 19】

在上一个连载里面，我们介绍了散度的定义，最后给出了矢量微分算子和散度的关系：

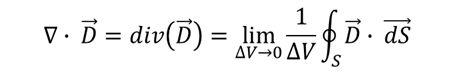
但是，为什么这个表达式可以成立呢？今天我们来证明一下（以直角坐标系为例）

注：今天的连载涉及的公式较多，实在不能理解可以跳过，不影响后续的阅读。

---

我们看下面这个矩形：

我们看这个长方体的最左下角的顶点 $M$，定义 $M(x,y,z)$，长方体的长宽高分别是 $△y,△x,△z$

在 $M$ 点处的矢量为：$A=A_x{a}_x+A_y{a}_y+A_z{a}_z$ 这里特别注意：$A_x,A_y,A_z$都是 $(x,y,z)$ 三者的函数！

我们下面先看看长方体前面的通量：$$\iint A\cdot a_{front}dS=\iint A_{x}dS=A_x(x+△x,y,z)△y△z$$
下面，我们回忆一下泰勒公式是怎么用的，下面是 $f(x)$ 在 $x_0$ 处的泰勒展开：$$f(x)=\frac{f(x_0)}{0!}+\frac{f^{\prime }(x_0)}{1!}(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\cdots$$
那么，类似地使用变量代换，将上式的 $x$ 代换成 $x+△x$，$x_0$ 换成 $x$，$f()$函数使用 $A_x()$替换，得：$$A_x(x+△x,y,z)=A_x(x,y,z)+\frac{\partial A_x(x,y,z)}{\partial x}△x+\frac{1}{2}\frac{{\partial }^2{A}_x(x,y,z)}{\partial x^2}△x^2+\cdots$$
因此，我们可以得到一个近似表达：$$A_x(x+△x,y,z)\approx A_x(x,y,z)+\frac{\partial A_x(x,y,z)}{\partial x}△x$$

因此，前面的净通量就近似表示成：$$\iint A\cdot a_{front}dS\approx A_x(x,y,z)△y△z+\frac{\partial A_x(x,y,z)}{\partial x}△x△y△z$$
那么，我们再看看后面得通量：由于 $A_x{a}_x$ 的方向是沿着 $x$ 轴的正方向，因此与 $a_{back}$ 的方向相反，那么得到的通量结果是：$$\iint A\cdot a_{back}dS=-A_x(x,y,z)△y△z$$

那么，我们就可以得到前后两个面的净通量：$$\begin{array}{rl}{\Phi }_{front}+{\Phi }_{back}& =A_x(x,y,z)△y△z+\frac{\partial A_x(x,y,z)}{\partial x}△x△y△z-A_x(x,y,z)△y△z\\ & =\frac{\partial A_x(x,y,z)}{\partial x}△x△y△z\end{array}$$

那么，如果我们求出前后左右上下六个面的净通量，就可以表示成：$${\Phi }_{total}=\frac{\partial A_x(x,y,z)}{\partial x}△x△y△z+\frac{\partial A_y(x,y,z)}{\partial y}△x△y△z+\frac{\partial A_z(x,y,z)}{\partial z}△x△y△z$$
令体积微元 $△V=△x△y△z$，因此得到闭合曲面净通量表达式：$${\Phi }_{total}=\frac{\partial A_x(x,y,z)}{\partial x}△V+\frac{\partial A_y(x,y,z)}{\partial y}△V+\frac{\partial A_z(x,y,z)}{\partial z}△V$$
把它重新带入散度的定义式，我们就可以得到散度的计算公式：$$\begin{array}{rl}divA& =\frac{\partial A_x(x,y,z)}{\partial x}+\frac{\partial A_y(x,y,z)}{\partial y}+\frac{\partial A_z(x,y,z)}{\partial z}\\ & =\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z}=▽A\end{array}$$

---

有了上面的证明，我们可以理直气壮地写出 $Maxwell$ 方程中描述静电场公式的微分形式啦：

---

那么我们想想 $Maxwell$ 方程中描述磁场的那个式子：

这不也是一样的形式嘛，只要是描述通量的，那么在微分形式里面我们就可以用散度描述他们：

那么至此，我们已经了解了对于闭合曲面积分的这种形式如何用微分形式描述——通过散度，那么我们知道 $Maxwell$ 方程里面还有闭合的线积分，那闭合线积分应该如何用微分形式描述呢？我们下一个连载好好说说。