数据结构(C语言版) 第二章 线性表 知识梳理+作业习题详解
目录
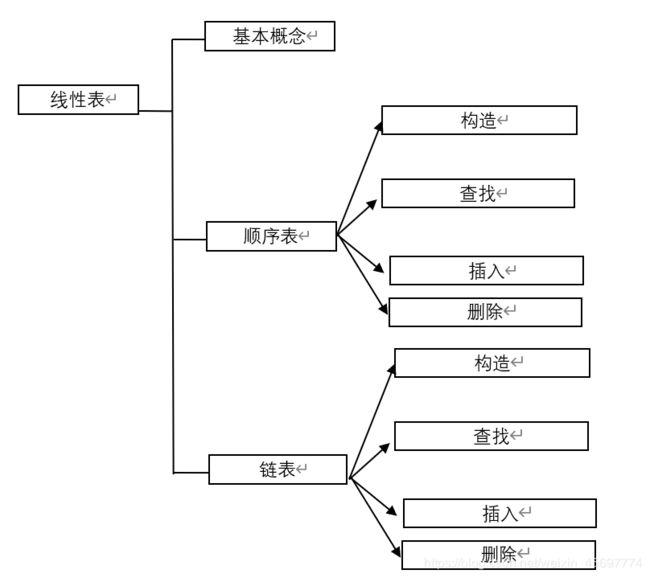
- 一、单链表顺序存储结构(顺序表)
- 0.单链表的基本概念
- 1.样例引入:多项式相加
- 二、单链表链式存储结构(链表)
- 0.链表的基本概念
- 1.前插法代码实例
- 2.链表尾插法完整代码附带各种操作
- 三、双向链表
- 0.双向链表的基本概念
- 1.双向链表的插入
- 2.双向链表的删除
- 四、顺序表和链表的比较
- 五、线性表的应用
- 0.有序表的合并
- 0.新建一个链表
- 1.直接合并
- 六、小结
- 七、相关作业习题
- 八、编程题
- 八、数据结构进阶
本系列博客为《数据结构》(C语言版)的学习笔记(上课笔记),仅用于学习交流和自我复习
数据结构合集链接: 《数据结构》C语言版(严蔚敏版) 全书知识梳理(超详细清晰易懂)
线性表的定义:
- 存在唯一一个“第一个”元素
- 存在唯一一个“最后一个”元素
- 除第一个元素外,每一个元素都有且只有一个前驱
- 除最后一个元素外,每个元素都有且只有一个后继
一、单链表顺序存储结构(顺序表)
0.单链表的基本概念
单链表强调元素在逻辑上紧密相邻,所以首先想到用数组存储。但是普通数组有着无法克服的容量限制,在不知道输入有多少的情况下,很难确定出一个合适的容量。对此,一个较好的解决方案就是使用动态数组。首先用malloc申请一块拥有指定初始容量的内存,这块内存用作存储单链表元素,当录入的内容不断增加,以至于超出了初始容量时,就用malloc扩展内存容量,这样就做到了既不浪费内存,又可以让单链表容量随输入的增加而自适应大小。
1.样例引入:多项式相加
A 17 ( x ) = 7 + 3 x + 9 x 8 + 5 x 17 A_{17}(x)=7+3x+9x^8+5x^{17} A17(x)=7+3x+9x8+5x17
B 8 ( x ) = 8 x + 22 x 7 − 9 x 8 B_8(x)=8x+22x^7-9x^8 B8(x)=8x+22x7−9x8
下面是顺序表的代码实现(建议不看,没什么营养 )
#include优点:
- 存储密度大(结点本身所占存储量/结点结构所占存 储量)
- 可以随机存取表中任一元素
缺点:
- 在插入、删除某一元素时,需要移动大量元素
- 浪费存储空间
- 属于静态存储形式,数据元素的个数不能自由扩充
二、单链表链式存储结构(链表)
0.链表的基本概念
建议每次写的时候都加一个头节点
各结点由两个域组成:
数据域:存储元素数值数据
指针域:存储直接后继结点的存储位置
- 结点:数据元素的存储映像。 由数据域和指针域两部分组成
- 链表: n 个结点由指针链组成一个链表。它是线性表的链式存储映像,称为线性表的链式存储结构
单链表、双链表、循环链表:
- 结点只有一个指针域的链表,称为单链表或线性链表
- 有两个指针域的链表,称为双链表
- 首尾相接的链表称为循环链表
头指针是指向链表中第一个结点的指针
首元结点是指链表中存储第一个数据元素a1的结点
头结点是在链表的首元结点之前附设的一个结点;数据域内只放空表标志和表长等信息
Q:1.如何表示空表?
有头结点时,当头结点的指针域为空时表示空表
Q:2. 在链表中设置头结点有什么好处
1.便于首元结点的处理 首元结点的地址保存在头结点的指针域中,所以在链表的第一个位置上的操作和其它位置一致,无须进行特殊处理;
⒉便于空表和非空表的统一处理
无论链表是否为空,头指针都是指向头结点的非空指针,因此空表和非空表的处理也就统一了。
头结点的数据域可以为空,也可存放线性表长度等附加信息,但此结点不能计入链表长度值。
结点在存储器中的位置是任意的,即逻辑上相邻的数据元素在物理上不一定相邻
这种存取元素的方法被称为顺序存取法
优点
- 数据元素的个数可以自由扩充
- 插入、删除等操作不必移动数据,只需修改链接指针,修改效率较高
缺点
- 存储密度小
- 存取效率不高,必须采用顺序存取,即存取数据元素时,只能按链表的顺序进行访问(顺藤摸瓜)
1.前插法代码实例
因为是前插法,所以是倒着顺序插入的(先入后出,先插入的在后面)
#include输入:
5
1 2 3 4 5
输出:
2 3 4 5
2.链表尾插法完整代码附带各种操作
链表完整代码链接:
我是链接QWQ
循环链表:表最后的一个节点的指针指向表头
三、双向链表
0.双向链表的基本概念
双链表顾名思义,就是链表由单向的链变成了双向链。 使用这种数据结构,我们可以不再拘束于单链表的单向创建于遍历等操作,大大减少了在使用中存在的问题。每一个节点都有两个指针分别指向该节点的前驱和后继。
定义:
struct DuLNode{
EtypedeflemType data; //数据域
struct DuLNode *prior; //前驱
struct DuLNode *next; //后继
}DuLNode, *DuLinkList
d->next->prior = d->prior->next = d
1.双向链表的插入
由于每个节点都有前驱和后继,所以插入的时候p节点及其前驱的前驱和后继都要更新。所以需要按顺序写四条语句更新。(新增结点别忘了给数据域赋值)
s->prior=p->prior;p->prior->next=s;s->next=p;p->prior=s;
2.双向链表的删除

删除一个结点,只需要把p结点的前驱的后继更新,p的后继的前驱更新,只需要两条语句即可。
p->prior->next=p->next;p->next->prior=p->prior;
顺便别忘了free(p);
§®©§
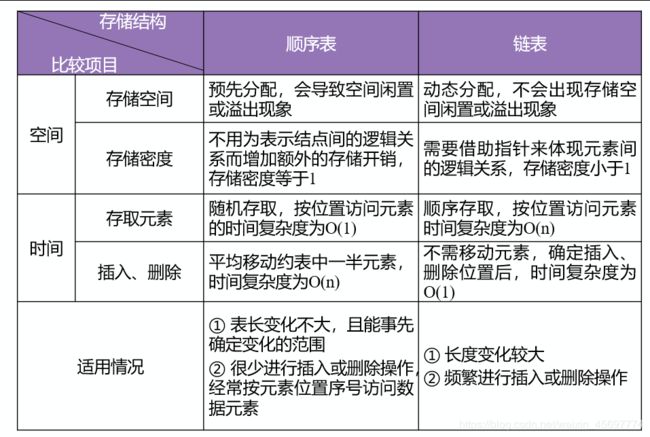
四、顺序表和链表的比较
五、线性表的应用
0.有序表的合并
已知线性表La 和Lb中的数据元素按值非递减有序排列,现要求将La和Lb归并为一个新的线性表Lc,且Lc中的数据元素仍按值非递减有序排列。
La=(1 ,7, 8)
Lb=(2, 4, 6, 8, 10, 11)
Lc=(1, 2, 4, 6, 7 , 8, 8, 10, 11)
0.新建一个链表
新建一个空表C,直接在A和B中每次选取最小值插入到C中,复杂度O(A.length+B.length),但是需要新开辟一个空表比较占用内存。
void MergeList_Sq(SqList LA,SqList LB,SqList &LC){
pa=LA.elem; pb=LB.elem; //指针pa和pb的初值分别指向两个表的第一个元素
LC.length=LA.length+LB.length; //新表长度为待合并两表的长度之和
LC.elem=new ElemType[LC.length]; //为合并后的新表分配一个数组空间
pc=LC.elem; //指针pc指向新表的第一个元素
pa_last=LA.elem+LA.length-1; //指针pa_last指向LA表的最后一个元素
pb_last=LB.elem+LB.length-1; //指针pb_last指向LB表的最后一个元素
while(pa<=pa_last && pb<=pb_last){ //两个表都非空
if(*pa<=*pb) *pc++=*pa++; //依次“摘取”两表中值较小的结点
else *pc++=*pb++; } pa++; //LB表已到达表尾
while(pb<=pb_last) *pc+
while(pa<=pa_last) *pc++=*+=*pb++; //LA表已到达表尾
}//MergeList_Sq
1.直接合并
只建一个新结点,相当于尾插法的end尾结点,而不是创建一个新链表,结点Pc每次指向A/B中最小值的结点,把两个链表连在一起(B连到A上面),不需要新开辟一个链表浪费空间,时间复杂度和上面的一样,都是暴力循环。(merge()函数表示很淦,合并两个有序序列本来就是merge要干的活 归并排序 )
void MergeList_L(LinkList &La,LinkList &Lb,LinkList &Lc){
pa=La->next; pb=Lb->next;
pc=Lc=La; //用La的头结点作为Lc的头结点
while(pa && pb){
if(pa->data<=pb->data){ pc->next=pa;pc=pa;pa=pa->next;}
else{pc->next=pb; pc=pb; pb=pb->next;}
pc->next=pa?pa:pb; //插入剩余段
delete Lb; //释放Lb的头结点}
六、小结
建议不看
- 掌握线性表的逻辑结构特性是数据元素之间存在着线性关系,在计算机中表示这种关系的两类不同的存储结构是顺序存储结构(顺序表)和链式存储结构(链表)。
- 熟练掌握这两类存储结构的描述方法,掌握链表中的头结点、头指针和首元结点的区别及循环链表、双向链表的特点等。
- 熟练掌握顺序表的查找、插入和删除算法
- 熟练掌握链表的查找、插入和删除算法
- 能够从时间和空间复杂度的角度比较两种存储结构的不同特点及其适用场合
七、相关作业习题
PTA上的好(po) 题
1.在带头结点的非空单链表中,头结点存储位置由头指针指示,首元素结点由头结点的NEXT域指示
答案:√
2.对于顺序表,以下说法错误的是( ) (2分)
A.顺序表是用一维数组实现的线性表,数组的下标可以看成是元素的绝对地址
B.顺序表的所有存储结点按相应数据元素间的逻辑关系决定的次序依次排列
C.顺序表的特点是:逻辑结构中相邻的结点在存储结构中仍相邻
D.顺序表的特点是:逻辑上相邻的元素,存储在物理位置也相邻的单元中
答案:A
习题二-线性表
3.设一个链表最常用的操作是在末尾插入结点和删除尾结点,则选用( )最节省时间。 (2分)
A单链表
B单循环链表
C带尾指针的单循环链表
D带头结点的双循环链表
答案:D
4.在循环链表中,将头指针改设为尾指针(rear)后,其头结点和尾结点的存储位置分别是( ) (2分)
Arear和rear->next->next
Brear->next 和rear
Crear->next->next和rear
Drear和rear->next
答案:B
5.线性表L=(a1, a2, … , an)用数组表示,假定删除表中任一元素的概率相同,则删除一个元素平均需要移动元素的个数是:
答案:n/2
6.以下为顺序表的定位运算,分析算法,请在方框处填上正确的语句。
int locate_sqlist(sqlist L,datatype X)
//在顺序表L中查找第一值等于X的结点。若找到回传该结点序号;否则回传0/
{
i=0;//(3分)
while((i≤L.last)&&(L.data[i-1]!=X))
i++;
if(L.Last==x)//(4分))
return i;
else return 0;
}
7.对单链表中元素按插入方法排序的C语言描述算法如下,其中L为链表头结点指针。请填充算法中标出的空白处。 5
typedef struct node
{
int data;
struct node *next;
}linknode,*link;
void Insertsort(link L)
{
link p,q,r,u;
p=L->next;
(1)______;
while((2)________)
{
r=L; q=L->next;
while((3)________&& q->data<=p->data)
{
r=q;
q=q->next;
}
u=p->next;
(4)______;
(5)______;
p=u;
}
}
答案:
(1) L->next=NULL
(2) p (或p!=NULL)
(3) q (或q!=NULL)
(4) p->next=r->next
(5) r->next=p
8.假设顺序表的长度为 n
若在位序 1 处删除元素,则需要移动 n-1 个元素;
若在位序 n 处删除元素,则需要移动 0 个元素;
若在位序 i(1≤i≤n) 处删除元素,则需要移动 n-i 个元素。
假设各位序删除元素的概率相同, 则平均需要移动 (n-1)/2 个元素。
这些题应该没什么需要讲的吧,其实都挺简单的。要是有不会的评论问我哦
八、编程题
List Merge( List L1, List L2 )
{
List L = (List)malloc(sizeof(struct Node));//新开一个,用来存答案记得分配内存先
List p1=L1 -> Next;
List p2=L2 -> Next;
List p3=L;
while(p1 && p2)
{
if(p1->Data <=p2->Data){
p3->Next=p1;
p3=p1;
p1=p1->Next;
}
else{
p3->Next=p2;
p3=p2;
p2=p2->Next;
}
}
if(p1==NULL)
p3->Next=p2;
if(p2==NULL)
p3->Next=p1;
L1->Next = NULL;//注意这一点!!!
L2->Next = NULL;//把它跟L(答案)断掉
return L;
}
八、数据结构进阶
上面的都是基础的知识,如果想要进阶学习一些更多的内容,可以点击下方博客链接:
0x13.基础数据结构—链表与邻接表
注:如果您通过本文,有(qi)用(guai)的知识增加了,请您点个赞再离开,如果不嫌弃的话,点个关注再走吧,日更博主每天在线答疑 ! 当然,也非常欢迎您能在讨论区指出此文的不足处,作者会及时对文章加以修正 !如果有任何问题,欢迎评论,非常乐意为您解答!( •̀ ω •́ )✧