一、4种插值方法及其误差估计
1、多项式插值(以单项式为基地)
(Ⅰ)解题思路
\[P_n(x)=a_0+a_1x+……+a_nx^n \]将\(\{x\}_{i=0}^n\)代入,构造出一个关于系数\(a_0,a_1,……,a_n\)的\(n+1\)元线性方程组,并解出\(\{a\}\)。
由于这种插值方法是最繁杂的,所以一般不会用到(除非在小学生面前装*),所以也不会考虑其误差,如果非得考虑的话,由
范德蒙德矩阵可知,矩阵非奇异所以\(P_n(x)\)存在且唯一,故而误差和其他插值方法的误差是一样的,这里就不做讨论了。
(Ⅱ)例题(参考《数值分析 第五版》\(P_{48}\ T_1\))
题目: 当\(x=1,-1,2\)时,\(f(x)=0,-3,4\),用单项式基底求\(f(x)\)的二次差值多项式。
解答:
构造插值函数:\(P_2(x)=a_0+a_1x+a_2x^2\),这时代入\(\{x\}_{i=0}^2\),得到如下的3元线性方程组:
\[\begin{cases} P_2(x_0)=a_0+a_1x_0+a_2x_{0}^2=0\\\\ P_2(x_1)=a_0+a_1x_1+a_2x_{1}^2=-3\\\\ P_2(x_2)=a_0+a_1x_2+a_2x_{2}^2=4 \end{cases} \Longrightarrow \begin{cases} P_2(1)=a_0+a_1+a_2=0\\\\ P_2(-1)=a_0-a_1+a_2=-3\\\\ P_2(2)=a_0+2a_1+4a_2=4 \end{cases} \]解得:
\[\begin{cases} a_0=-\ \frac{7}{3}\\\\ a_1=\quad\frac{3}{2}\\\\ a_2=\quad\frac{5}{6} \end{cases} \]所以最后得出插值函数:\(P_2(x)=-\frac{7}{3}+\frac{3}{2}x+\frac{5}{6}x^2\)。
2、拉格朗日插值法
(Ⅰ)解题思路
\[L_n(x)=\sum_{i=0}^n{f(x_i)\times\frac{(x-x_0)…(x-x_{j-1})(x-x_{j+1})…(x-x_n)}{(x_j-x_0)…(x_j-x_{j-1})(x_j-x_{j+1})…(x_j-x_n)}} \]\[R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}\times\omega_{n+1}(x),\xi\in(a,b) \]所以线性插值的函数和误差估计为:
\[L_1(x)={f(x_0)\times\frac{(x-x_1)}{(x_0-x_1)}+f(x_1)\times\frac{(x-x_0)}{(x_1-x_0)}} \]\[R_1(x)=\frac{f^{(2)}(\xi)}{2}\times(x-x_0)(x-x_1),\xi\in(x_0,x_1) \]二次插值的函数和误差估计为:
\[L_2(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}\times f(x_0)+\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}\times f(x_1)+\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}\times f(x_2) \]\[R_2(x)=\frac{1}{3!}f^{(3)}(\xi)(x-x_{0})(x-x_{1})(x-x_{2}) \]有上述的误差分析可以看到,\(n\)阶拉格朗日插值法对\(n\)阶及其以下的\(f(x)\)都准确成立,所以精度为\(n\)。
(Ⅱ)例题
例题1(参考《数值分析 第五版》\(P_{48} T_1\))\(\Longrightarrow\) 解出插值函数
题目: 当\(x=1,-1,2\)时,\(f(x)=0,-3,4\),用拉格朗日插值基底求\(f(x)\)的二次差值多项式。
解答:
\[\begin{cases} &l_0(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}=-\ \frac{1}{2}(x+1)(x-2)\\\\ &l_1(x)=\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}=\quad\frac{1}{6}(x-1)(x-2)\\\\ &l_2(x)=\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}=\quad\frac{1}{3}(x-1)(x+1) \end{cases} \]所以解得\(L_2(x)=-\frac{1}{2}(x+1)(x-2)+\frac{1}{6}(x-1)(x-2)+\frac{1}{3}(x-1)(x+1)\)。
例题2(参考《数值分析 第五版》\(P_{48} T_4\))\(\Longrightarrow\) 拉格朗日插值的精度
题目: 设\(x_j\)为互异节点(\(j=0,1,…,n\)),求证:\(\sum_{j=0}^{n}{[x_j^k\times l(x_j)]}\equiv x^k\),\(k=0,1…n\)。
解答:
根据拉格朗日插值函数模型,我们不妨设\(f(x)=x^k\);也就是说我们证的是\(L_n(x)\equiv f(x)\),即证\(R_n(x)\equiv0\);根据拉格朗日插值的误差估计,我们不难得出\(R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}\times\omega_{(n+1)}(x)\);这个时候考察\(f^{(n+1)}(\xi)\),由于\(f(x)=x^k\)为\(k\)阶多项式,并且\(k\le n\),所以\(f^{(n+1)}(\xi)\equiv0\),故而\(R_n(x)\equiv0\),证毕;
总结: 此题可以得出结论——\(n\)阶拉格朗日插值多项式的精度为\(n\),也就是对\(n\)阶以内的函数都准确成立;
例题3(参考《数值分析 第五版》\(P_{48} T_5\))\(\Longrightarrow\) 拉格朗日插值中线性插值的误差分析
题目: 设\(f(x)\in C^2[a,b]\)且\(f(a)=f(b)=0\),求证:\(\underset{a\le x\le b}{max}|f(x)|\le\frac{1}{8}(b-a)^2\times\underset{a\le x\le b}{max}|f^{(2)}(x)|\)。
解答:
很显然,只给了两个点,正好两个插值条件,所以我们使用线性插值方法,构造线性插值函数:
\[L_1(x)={f(x_0)\times\frac{(x-x_1)}{(x_0-x_1)}+f(x_1)\times\frac{(x-x_0)}{(x_1-x_0)}}=0 \]所以\(f(x)=L_1(x)+R_1(x)=R_1(x)=\frac{f^{(2)}(\xi)}{2}\times(x-a)(x-b),\xi\in(a,b)\);所以考虑到\((x-a)(x-b)\)在\((a,b)\)上的最大值在\(x=\frac{a+b}{2}\)处,值为\((\frac{b-a}{2})^2\),所以即可得出结论:\(\underset{a\le x\le b}{max}|f(x)|\le\frac{1}{8}(b-a)^2\times\underset{a\le x\le b}{max}|f^{(2)}(x)|\),证毕。
总结: 把握线性插值的误差估计,\(\omega_{n+1}(x)\)在中点出去的最大值。顺便掌握\(n\)阶拉格朗日插值的误差。
例题4(参考《数值分析 第五版》\(P_{48} T_6\))\(\Longrightarrow\) 拉格朗日插值中二次插值的误差分析
题目: 在\(-4\le x\le4\)给出\(f(x)=e^x\)的等距节点函数表,若用二次差值求\(e^x\)的近似值,要使截断误差不超过\(10^{-6}\),求出函数表的步长\(h\)应取多少?
解答:
\[R_h(x)=\frac{1}{3!}f^{(3)}(\xi)(x-x_{i-1})(x-x_{i})(x-x_{i+1}) \]令\(x=x_i+th\),则\(x_{i-1},x_i,x_{i+1}\)分别对应\(t=-1,0,1\),故而有:
\[(x-x_{i-1})(x-x_{i})(x-x_{i+1})=(t-1)t(t+1)h^3 \]要求是截断误差不超过\(10^{-6}\),所以只要误差限不超过\(10^{-6}\)即可,而误差限就是\(|R_h(x)|\)的最大值。设函数:\(\psi(t)=(t-1)t(t+1)\),现在分别考虑\(f^{(3)}(\xi)\)和\(\psi(t)\)的最大值。
对\(\psi(t)\)求一阶导可得:\(\psi^{'}(t)=3t^2-1\),所以有\(|\psi(t)|\)在\([0,1]\)上的最大值为\(|\psi(\frac{1}{\sqrt{3}})|=\frac{2\sqrt{3}}{9}\);
\(\underset{-4\le x\le4}{max}|f^{(3)}(x)|=\underset{-4\le x\le4}{max}|e^x|=|e^4|=54.60\);
所以得出\(\underset{-4\le x\le4}{max}|R_h(x)|=\frac{\sqrt{3}}{27}\cdot54.60\times h^3\le10^{-6}\Longrightarrow h\le0.0066\);
总结: 看似有步长,为分段插值,其实本质上就是分析拉格朗日插值法的误差,熟练掌握拉格朗日插值法的误差估计:\(R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)}\times\omega_{n+1}(x)\),通过代入给出的\(f(x)\)的表达式来判断\(f^{(n+1)}(\xi)\)的最大值,并结合\(\omega_{n+1}(x)\)的最大值(此处一般都是整一个步长\(h=\underset{k}{max}\ h_k\),然后将\(x_i\)和\(x\)替换掉,构造成一个\(t\)的函数),从而确定出\(n\)阶拉格朗日插值多项式的误差限。
3、牛顿插值
(Ⅰ)解题思路
牛顿插值有两种表达形式:
均差形式的牛顿插值和差分形式的牛顿插值。第一种:均差形式的牛顿插值
\[\begin{equation}\begin{aligned}P_n(x) &= f(x_0)+f[x_0, x_1]·(x-x_0)+f[x_0, x_1, x_2]·(x-x_0)(x-x_1)+...+f[x_0, x_1, ..., x_n]·(x-x_0)(x-x_1)...(x-x_{n-1})\end{aligned}\end{equation} \]\[R_n(x) = f[x, x_0, x_1, ..., x_n]·\omega_{n+1}(x) \]只有各阶的均差我们是不知道的,但是我们可以通过构造均差表来求得。
并且值得注意的一点是:在高阶均差中的同阶均差相差不多,可以近似相等,这可以简化求误差限;同样也正是因为这个原因,我们在求误差限的时候通常是将\(f[x, x_0, x_1, ..., x_n]\)换成\(f[x_0, x_1, ..., x_n,x_{n+1}]\),也就是说我们需要\(n+2\)个点才能估计出
均差形式的误差限。
第二种:差分形式的牛顿插值(牛顿前插公式)
\[P_n(x_0+th) = f_0+t\Delta f_0+\frac{t(t-1)}{2!}\Delta^2f_0+…+\frac{t(t-1)…(t-n+1)}{n!}\Delta^nf_0 \]\[R_n(x) = \frac{t(t-1)…(t-n+1)}{(n+1)!}h^{n+1}f^{(n+1)}(\xi),其中\xi \in [x_0, x_n] \]同样的,我们可以通过构造差分表来获取\(x_0\)点处的各阶差分。
与
均差形式的牛顿插值不同,差分形式的牛顿插值在解算误差限的时候只需要\(n+1\)个点。不过我们依然可以看到,差分形式是由均差形式通过“均差-差分”(\(f[x_k, ..., x_{k+m}] = \frac{1}{m}\frac{1}{h^m}\Delta^mf_k,其中m=1,2,...,n\))以及“差分-导数”(\(\Delta^nf_k = h^nf^{(n)}(\xi)\),其中\(\xi \in [x_k, x_{k+n}]\))这两层关系推出来的,也就是说将\(f[x, x_0, x_1, ..., x_n]\)换成了\(f^{(n+1)}(\xi)\),这样就要求\(f(x)\)的\(n+1\)阶导数。
总结: 当插值函数是一个复杂函数(这里的复杂指的是原函数的导数不容易得出)时,如:\(f(x)=\sqrt{\frac{\cos x+2\sin x}{2\cos x-\sin x}}\),想求\(n+1\)阶导数几乎是不存在的(除非你是徐半仙或者聂星人或者许外挂),这是我们就只能通过构造
均差表来解算其误差限;当插值函数是一个简单函数时,如\(f(x)=\cos x\),这时求\(n+1\)阶导数赶赶单单没有\(len\)何挑战,所以就可以构造差分表来解算误差限。一般地,题目中应该会给我们\(n+2\)个点来研究\(n\)次的牛顿插值。但是如果题目中的原函数是复杂函数,并且只给了\(n+1\)个点,这个时候我们不用慌,还有\(PlanB\)——题目肯定是要我们求\(f(m)\)的近似值,其中\(m\in(x_0,x_n)\),这个时候就相当于给了我们第\(n+2\)个点:\(m\),我们就能够通过\(f(m)\)的值(代入表达式中获得的近似值)来求得\(f[x, x_0, x_1, ..., x_n]\)。
(Ⅱ)例题
例题1(参考《数值分析 第五版》\(P_{32} 例题4\))\(\Longrightarrow\)
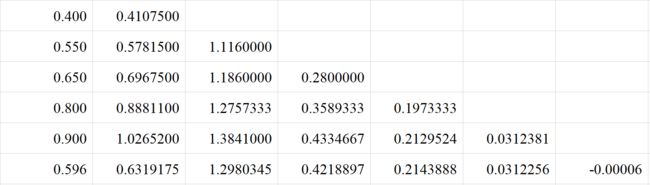
均差形式的牛顿插值及其误差估计题目: 给出\(f(x)\)的函数表求4次牛顿插值多项式,并由此计算\(f(0.596)\)的近似值及其误差限。
解答:
首先根据给定函数表构造《函数-均差表》:
\(x\) \(f(x)\) \(\Delta f^{(1)}\) \(\Delta f^{(2)}\) \(\Delta f^{(3)}\) \(\Delta f^{(4)}\) \(\Delta f^{(5)}\) \(0.40\) \(\underline{0.41075}\) \(0.55\) \(0.57815\) \(\underline{1.11600}\) \(0.65\) \(0.69675\) \(1.18600\) \(\underline{0.28000}\) \(0.80\) \(0.88811\) \(1.27573\) \(0.35893\) \(\underline{0.19733}\) \(0.90\) \(1.02652\) \(1.38410\) \(0.43348\) \(0.21300\) \(\underline{0.03134}\) \(1.05\) \(1.25382\) \(1.51533\) \(0.52493\) \(0.22863\) \(0.03126\) \(-\ 0.00012\) \[\begin{equation}\begin{aligned}P_n(x) &= f(x_0)+f[x_0, x_1]·(x-x_0)+f[x_0, x_1, x_2]·(x-x_0)(x-x_1)+...+f[x_0, x_1, ..., x_n]·(x-x_0)(x-x_1)...(x-x_{n-1})\end{aligned}\end{equation} \]所以我们可以得到:
\[\begin{equation}\begin{aligned} P_4(x) &= \quad0.41075+1.11600\cdot(x-0.40)+0.28000\cdot(x-0.40)(x-0.55)\\&+\quad0.19733\cdot(x-0.40)(x-0.55)(x-0.65)\\ &+\quad 0.03134\cdot(x-0.40)(x-0.55)(x-0.65)(x-0.80) \end{aligned}\end{equation} \]所以有:\(f(0.596)\approx P_4(0.596)=0.63192\ 3237\),另外我们有截断误差为:
\[|R_4(x)| = |f[x, x_0, x_1, ..., x_4]·\omega_{5}(0.596)|\approx |f[x_0, x_1, ..., x_5]·\omega_{5}(0.596)|\le3.63\times10^{-9} \]\(PlanB\):
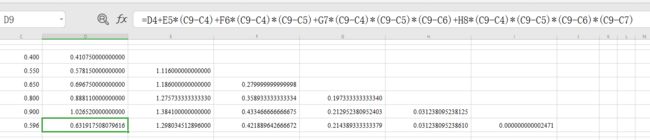
以下内容了解即可,考试时一般用不着!!!
大家不难发现,我这里保留了小数点后15位,那是不是保留10位或者更小的有效数字就为0了呢?我们不妨来看一下保留5位和7位的情况:
保留小数点后5位: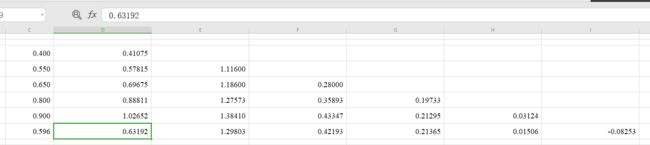
保留小数点后7位:大家不难发现,结果并不是我们想象的那样简单,有效位数对误差影响是非常非常大的,正所谓“差之毫厘谬以千里”,但是我们不用慌,因为如图所示(天机就是拿来泄漏的):
所以大家就按部就班即可,题目还是很严谨的!!!
例题2(参考《数值分析 第五版》\(P_{34} 例题5\))\(\Longrightarrow\)
差分形式的牛顿插值及其误差估计题目: 给出\(f(x)=\cos x\)在\(x_k=kh\)(k=0,1,…,5\(、\)h=0.1\()处的函数值,试用4次牛顿前插公式计算\)\(f(0.048)\)的近似值并估计误差。
解答:
首先构造
差分表,并用牛顿前插公式:由\(x=x_0+th\Longrightarrow t=\frac{x-x_0}{h}=0.48\);所以有
\[\begin{aligned}\cos(0.048)\approx P_4(0.048)&=1.00000+0.48\times(-0.00500)+\frac{0.48\cdot(0.48-1)}{2!}\times(-0.00993)\\&+\frac{0.48\cdot(0.48-1)\cdot(0.48-2)}{3!}\times(0.00013)\\&+\frac{0.48\cdot(0.48-1)\cdot(0.48-2)\cdot(0.48-3)}{4!}\times(0.00012)\\&=0.99885\end{aligned} \]其误差限函数为:
\[|R_4(x)| = \frac{t(t-1)(t-2)(t-3)(t-4)}{5!}h^{5}f^{(5)}(\xi),其中\xi \in [x_0, x_n] \]所以有:
\[|R_4(0.0480)| \le \frac{0.48(0.48-1)(0.48-2)(0.48-3)(0.48-4)}{5!}(0.1)^{5}\times|\sin(0.5)|\le1.3433\times10^{-7} \]
总结:
均差表可以不用原函数求\(n+1\)阶导数,但是它的缺点就是难算,而且估计误差的时候需要\(n+2\)个点;
差分表的制作过程比均差表简单得多,而且可以不用第\(n+2\)个点就能估计出误差限,前提是原函数的导数必须是能求出来的;
4、埃尔米特插值
(Ⅰ)整理思绪:埃尔米特插值与牛顿插值的联系
这也就是说埃尔米特插值就是牛顿插值的一种特殊情况,两点三次埃尔米特插值和\(n\)点\(n\)次埃尔米特插值是埃尔米特插值的两种常用模型;而且一般也就是靠这两种(除非有人想要你并让你)。
(Ⅱ)解题思路
普通的牛顿插值在此前已经研究完了,现在我们开始研究埃尔米特插值的套路。
(1)套路2(普通的埃尔米特插值): 给出了\(m+1\)个插值条件【含函数值(\(k+1\)个)和导数值(\(n-k\)个)】构造出不超过\(m\)次的埃尔米特插值多项式。【顺便提一嘴:书上有说不给一般埃尔米特插值的公式,因为这没必要】。
由于之前有说“埃尔米特插值就是牛顿插值的特殊情况”,那么很显然,这句话的意思就是埃尔米特插值也遵循牛顿插值的套路——套路1。在这里我们就有了两套方案:
\(PlanA\): 我亲切地称之为“牛顿插值附身法”(因为和牛顿插值简直一模一样)
构造函数表和均差表,重结点就替换为导数,啥一阶导、二阶导统统安排上(现在感觉十分挠头没关系,之后有例子和详细步骤,所以不用慌张)。
\(PlanB\): 我愿称之为“暴力硬核待定系数法”(真的很暴力,一般也就3点3次埃尔米特插值用)
用所有的点(不包含其他重节点,意思就是只能每一组重节点中只能有一个入选)构造一个《函数-均差表》,然后写出插值函数,这个插值函数十年小母——老了,一共是分为俩部分:牛顿插值函数和待定系数高阶多项式。
牛顿插值函数 依据\(PlanB\)中构造的均差表得到的牛顿插值函数;
待定系数高阶多项式 由于不是\(n+1\)个点,所以
牛顿插值函数必然到不到\(n\)阶,这是我们就需要待定系数,并且按照牛顿插值函数构造的规则来填补剩下的高阶多项式。如果是\(n\)点\(n\)次埃尔米特插值函数,那么就直接在\(n-1\)阶牛顿插值函数后面利用第\(n\)个点:\(P_n(x)=P_{n-1}(x)+A\times(x-x_0)…(x-x_n)\)。其误差估计当然就可以用
牛顿插值的误差估计了,不过值得注意的是我们用的牛顿前插公式,而且将步长与\((t-i+1)\)进行了合并,重新得到了\((x-x_i)\):\[R_n(x)=\frac{1}{(n+1)!}\cdot f^{(n+1)}(\xi)\times\prod_{i=0}^k(x-x_i)^{j_i} \]其中\(j_i\)表示第\(x_i\)这个点出现的次数,比如如果不是重节点那么该值就为1。
(2)套路3(两点三次埃尔米特插值): 有两个节点,在这两个节点上,原函数函数值与插值函数函数值相等(\(f(x_i)=P(x_i)\)),并且对应的导数值也相等(\(f^{(1)}(x_i)=P^{(1)}(x_i)\))。直接给出公式:
\[\begin{aligned}H_3(x)=&(1+2\cdot\frac{x-x_k}{x_{k+1}-x_k})(\frac{x-x_{k+1}}{x_k-x_{k+1}})^2\cdot y(x_k)+(1+2\cdot\frac{x-x_{k+1}}{x_k-x_{k+1}})(\frac{x-x_{k}}{x_{k+1}-x_k})^2\cdot y(x_{k+1})\\\\&+({x-x_k})(\frac{x-x_{k+1}}{x_k-x_{k+1}})^2\cdot y^{'}(x_k)+({x-x_{k+1}})(\frac{x-x_{k}}{x_{k+1}-x_{k}})^2\cdot y^{'}(x_{k+1})\end{aligned} \]其误差估计为:
\[R_3(x)=\frac{f^{(4)}(\xi)}{4!}(x-x_k)^2(x-x_{k+1})^2\qquad\xi\in(x_k,x_{k+1}) \]
(Ⅲ)例题
例题1(参考《数值分析 第五版》\(P_{49} T_{13}\))\(\Longrightarrow\) 套路2(普通的埃尔米特插值)
题目: 求次数小于等于3的多项式\(P_3(x)\),是满足条件\(P_3(x_0)=f(x_0)\)、\(P_3^{(1)}(x_0)=f^{(1)}(x_0)\)、\(P_3^{(2)}(x_0)=f^{(2)}(x_0)\)、\(P_3(x_1)=f(x_1)\)。
解答:
可以看到这虽然是“两点三次埃尔米特插值”,但是此非彼,所以初步判定此题为题;
此题是“普通埃尔米特插值”,所以有两种解法(突然发现一箭双雕):
\(PlanA\): “牛顿插值附身法”
构建《函数-均差表》:
\(x\) \(f(x)\) 一阶均差 二阶均差 三阶均差 \(x_0^{(1)}\) \(f(x_0)^{(1)}\) \(x_0^{(2)}\) \(f(x_0)^{(2)}\) \(f^{(1)}(x_0)^{(1)}\) \(x_0^{(3)}\) \(f(x_0)^{(3)}\) \(f^{(1)}(x_0)^{(2)}\) \(\frac{f^{(2)}(x_0)}{2}\) \(x_1\) \(f(x_1)\) \(f[x_0,x_1]\) \(\frac{f[x_0,x_1]-f^{(1)}(x_0)}{x_1-x_0}\) \(\frac{\frac{f[x_0,x_1]-f^{(1)}(x_0)}{x_1-x_0}-\frac{f^{(2)}(x_0)}{2}}{x_1-x_0}\) 这些东西一般都是已知的,只要带进去算(反正我是不建议找规律带公式的),还是一个一个算吧,这公式忒难记了。
然后直接用牛顿插值就好了,这里我就不写了,没多大个意义。
直接给出答案:
\[P_3(x)=f(x_0)+f^{'}(x_0)\times(x-x_0)+\frac{1}{2}f^{''}(x_0)\times(x-x_0)^2+[\frac{f[x_0,x_1]-f^{'}(x_0)}{x_1-x_0}-\frac{1}{2}f^{''}(x_0)]\times\frac{(x-x_0)^3}{x_1-x_0} \]\(PlanB\): “暴力硬核待定系数法”
构造《函数-均差表》:
\(x\) \(f(x)\) 一阶均差 \(x_0\) \(f(x_0)\) \(x_1\) \(f(x_1)\) \(f[x_0,x_1]\) 然后构造函数:
\[P_3(x)=f(x_0)+f[x_0,x_1]\cdot(x-x_0)+A\times(x-x_0)(x-x_1)+B\times(x-x_0)^2(x-x_1) \]\[P_3^{(1)}(x)=f[x_0,x_1]+A\times[2x-(x_0+x_1)]+B\times[(x-x_0)^2+2(x-x_0)(x-x_1)] \]\[P_3^{(2)}(x)=2A+B\times[2(x-x_0)+2\cdot[2x-(x_0+x_1)]] \]将\(P_3^{(1)}(x_0)=f^{(1)}(x_0)\)、\(P_3^{(2)}(x_0)=f^{(2)}(x_0)\)分别代入可得:
\[P_3^{(1)}(x_0)=1+A\times(x_0-x_1)=f^{(1)}(x_0) \]\[P_3^{(2)}(x_0)=2A+B\times[2\cdot(x_0-x_1)]=f^{(2)}(x_0) \]解得:
\[A=\frac{f^{(1)}(x_0)-f[x_0,x_1]}{x_0-x_1},\qquad B=\frac{f^{(2)}(x_0)\times(x_0-x_1)-2[f^{(1)}(x_0)-f[x_0,x_1]]}{2(x_0-x_1)^2} \]代入函数,可得:
\[\begin{aligned}P_3(x)&=f(x_0)+f[x_0,x_1]\cdot(x-x_0)\\\\&+\frac{f^{(1)}(x_0)-f[x_0,x_1]}{x_0-x_1}\times(x-x_0)(x-x_1)\\\\&+\frac{f^{(2)}(x_0)\times(x_0-x_1)-2[f^{(1)}(x_0)-f[x_0,x_1]]}{2(x_0-x_1)^2}\times(x-x_0)^2(x-x_1)\end{aligned} \]不妨整理一下(将\(x-x_1\Longrightarrow x-x_0+x_0-x_1\)),易得(放,难得一批):
\[P_3(x)=f(x_0)+f^{'}(x_0)\times(x-x_0)+\frac{1}{2}f^{''}(x_0)\times(x-x_0)^2+[\frac{f[x_0,x_1]-f^{'}(x_0)}{x_1-x_0}-\frac{1}{2}f^{''}(x_0)]\times\frac{(x-x_0)^3}{x_1-x_0} \]\(PlanC\): 没啥好名儿了,就暂定为“牛顿待定系数法”吧
惊不惊喜,意不意外,没想到我还有第三种方法叭(
)。这是针对于仅仅不知道最高阶的均差(或者说不想直接从表中求得)并且该点不是重节点。之所以说一般为最后一项,是因为如果前面不知道后面的均差一般也无从得知,这是一个一环扣一环的过程。
首先我们依据\(PlanB\)中构造的《函数-均差表》,所以有:
\(x\) \(f(x)\) 一阶均差 二阶均差 三阶均差 \(x_0^{(1)}\) \(f(x_0)^{(1)}\) \(x_0^{(2)}\) \(f(x_0)^{(2)}\) \(f^{(1)}(x_0)^{(1)}\) \(x_0^{(3)}\) \(f(x_0)^{(3)}\) \(f^{(1)}(x_0)^{(2)}\) \(\frac{f^{(2)}(x_0)}{2}\) \(x_1\) \(f(x_1)\) \(f[x_0,x_1]\) \(f[x_0,x_0,x_1]\) \(f[x_0,x_0,x_0,x_1]\) 然后发现只有第三节均差我们是不知道的,由于在牛顿插值的时候其实最后一个点是用不上的,但是插值函数很显然是通过这个点的,所以先构造插值函数(设\(f[x_0,x_0,x_0,x_1]=A\)):
\[P_3(x)=f(x_0)+f^{'}(x_0)\times(x-x_0)+\frac{1}{2}f^{''}(x_0)\times(x-x_0)^2+A\times{(x-x_0)^3} \]再将最后一个点代入函数,解得:
\[A=[\frac{f[x_0,x_1]-f^{'}(x_0)}{x_1-x_0}-\frac{1}{2}f^{''}(x_0)]\times\frac{1}{x_1-x_0} \]所以最后还是可以得到插值函数为:
\[P_3(x)=f(x_0)+f^{'}(x_0)\times(x-x_0)+\frac{1}{2}f^{''}(x_0)\times(x-x_0)^2+[\frac{f[x_0,x_1]-f^{'}(x_0)}{x_1-x_0}-\frac{1}{2}f^{''}(x_0)]\times\frac{(x-x_0)^3}{x_1-x_0} \]总结: 像套路2(普通埃尔米特插值函数)一共有三种解法
①、最朴素的解法(\(PlanA\):牛顿插值附身法): 将所有的点(包含重节点)都放入《函数-均差表》中,用牛顿插值法的思想解出函数的表达式。优点——一步一步无脑代入、缺点——繁琐;
②、最暴力的解法(\(PlanB\):暴力硬核待定系数法): 将所有点(不包含其他重节点)放入《函数-均差表》中,先用牛顿插值法写出前半部分,然后再用待定系数法构造出后半部分的高阶多项式。最后将导数值的差之条件代入,并解出各个待定的系数。优点——由于插值的时候不考虑重节点,所以对计算机更加友好、缺点——常识告诉我们暴力的方法只有计算机能胜任
;
③、当朴素和暴力擦除爱情的火花时(\(PlanC\):牛顿待定系数法): 当满足一下两个条件时才能触发:
只有一项均差不知道&&这一项对应的节点不能是重节点。这种情况及其罕见,除非有人刻意安排(就像爱情一样),所以大家一定要长点儿心,不要和这玩意儿失之交臂。通过待定系数构造出插值函数之后,将所求点代入方程接触系数。
例题2(参考《数值分析 第五版》\(P_{49} T_{14}\))\(\Longrightarrow\) 套路3(两点三次埃尔米特插值)
题目: 求小于等于3的多项式\(P_3(x)\)使其满足条件\(P_3(0)=0\)、\(P_3^{'}(0)=1\)、\(P_3(1)=1\)、\(P_3^{'}(1)=2\)。
解答:
\[\begin{aligned}H_3(x)=&(1+2\cdot\frac{x-x_k}{x_{k+1}-x_k})(\frac{x-x_{k+1}}{x_k-x_{k+1}})^2\cdot y(x_k)+(1+2\cdot\frac{x-x_{k+1}}{x_k-x_{k+1}})(\frac{x-x_{k}}{x_{k+1}-x_k})^2\cdot y(x_{k+1})\\\\&+({x-x_k})(\frac{x-x_{k+1}}{x_k-x_{k+1}})^2\cdot y^{'}(x_k)+({x-x_{k+1}})(\frac{x-x_{k}}{x_{k+1}-x_{k}})^2\cdot y^{'}(x_{k+1})\end{aligned} \]直接代入,无脑求解:
\[\begin{aligned}P_3(x)&=(1+2\cdot\frac{x-0}{1-0})(\frac{x-1}{0-1})^2\cdot 0+(1+2\cdot\frac{x-1}{0-1})(\frac{x-0}{1-0})^2\cdot 1\\\\&+({x-0})(\frac{x-1}{0-1})^2\cdot 1+({x-1})(\frac{x-0}{1-0})^2\cdot 2\\\\&=x^2(3-2x)+x(x-1)^2+2x(x-1)=x^3-x^2+x\end{aligned} \]总结: 像这种题一般都是无脑题,只要翻翻书就知道答案了(但是知道和算对永远是两码事);
例题3(参考《数值分析 第五版》\(P_{49} T_{16}\))\(\Longrightarrow\) 套路3(两点三次埃尔米特插值)— 埃尔米特与牛顿
题目: 求一个不高于4次的多项式\(P_4(x)\),使它满足\(P_4(0)=P_4^{'}(0)=0\)、\(P_4(1)=P_4^{'}(1)=1\)、\(P_4(2)=1\)。
解答: 重点—埃尔米特插值是一种特殊的牛顿插值
所以我们可以依据条件:\(P_4(0)=P_4^{'}(0)=0\)和\(P_4(1)=P_4^{'}(1)=1\),可以无脑得到两点三次的埃尔米特插值多项式\(H_3(x)=x^2(2-x)\);又已知\(P_4(x)\)不高于4次,所以根据牛顿插值的改正思想构造函数:
\[P_4(x)=H_3(x)+A(x-0)^2(x-1)^2 \]最后将最后一个点(想到套路2中的\(PlanC\))代入式中解得\(A=\frac{1}{4}\),故而得出插值函数为:
\[P_4(x)=x^2(2-x)+\frac{1}{4}x^2(x-1)^2=\frac{1}{4}x^2(x-3)^2 \]总结: 埃尔米特插值是一种特殊的牛顿插值,可以运用改正的思想,并且巧妙的结合套路2中的\(PlanC\),把握机会。
例题3(参考《数值分析 第五版》\(P_{49} T_{15}\))\(\Longrightarrow\) 套路3(两点三次埃尔米特插值)— 误差分析
题目: 证明两点三次埃尔米特的余项为\(R_3(x)=\frac{1}{4!}\cdot f^{(4)}(\xi)\times(x-x_k)^2(x-x_{k+1})^2,\xi\in(x_k,x_{k+1})\)。
解答: 让你记你就记着,你是十万个为什么蛮?
总结: 其实这个余项可以从牛顿前插公式余项中瞥见端倪,给出牛顿插值余项:\(R_n(x)=\frac{1}{(n+1)!}\cdot f^{(n+1)}(\xi)\times\prod_{i=0}^k(x-x_i)^{j_i}\),很显然\(n=3,j_1=j_2=2\),所以就有了两点三次埃尔米特插值的误差估计。
5、分段低次插值
(Ⅰ)解题思路: 掌握前面4种插值方法。
(Ⅱ)例题:
例题1(参考《数值分析 第五版》\(P_{49} T_{18}\))分段线性插值
主要掌握一点:
\[I_h(x)=\sum_{i=0}^n(f(x_i)\cdot l_i(x)) \]而其中有:(\(x=x_i\)分别对应了两段插值函数)
\[l_i(x)=\begin{cases}&\frac{x-x_{i-1}}{x_i-x_{i-1}}=\frac{1}{h}\times(x-x_{i-1}),x_{i-1}\le x\lt x_i\\\\&\frac{x-x_{i+1}}{x_i-x_{i+1}}=\frac{1}{h}\times(x_{i+1}-x),x_{i}\le x\lt x_{i+1}\\\\&0,其他\end{cases} \]误差分析为:
\[R_1(x)=\frac{1}{2}\cdot f^{''}(\xi)\times(x-x_i)(x-x_{i+1}) \]所以误差限为:
\[\underset{a\le x\le b}{max}|R_{(1,h)}(x)|=\frac{1}{2}\cdot\underset{a\le x\le b}{max}{|f^{''}(x)|}\times(\frac{x_{i+1}-x_i}{2})^2=\frac{1}{8}\cdot\underset{a\le x\le b}{max}{|f^{''}(x)|}\times h^2 \]
例题2(参考《数值分析 第五版》\(P_{49} T_{19}\))两点三次埃尔米特插值
与上述同理,构造分段插值函数:
\[I_h(x)=\sum_{i=0}^n[\alpha_i(x)f(x_i)+\beta_i(x)f^{'}(x_i)] \]其中有:
\[\alpha_i(x)=\begin{cases}&(1+2\cdot\frac{x-x_{i}}{x_{i-1}-x_{i}})(\frac{x-x_{i-1}}{x_{i}-x_{i-1}})^2,x_{i-1}\le x\lt x_i\\\\&(1+2\cdot\frac{x-x_{i}}{x_{i+1}-x_i})(\frac{x-x_{i+1}}{x_{i}-x_{i+1}})^2,x_{i}\le x\lt x_{i+1}\end{cases},\qquad\beta_i(x)=\begin{cases}({x-x_i})(\frac{x-x_{i-1}}{x_i-x_{i-1}})^2,x_{i-1}\le x\lt x_i\\\\({x-x_{i}})(\frac{x-x_{i+1}}{x_{i}-x_{i+1}})^2,x_{i}\le x\lt x_{i+1}\end{cases} \]误差分析:
\[\underset{a\le x\le b}{max}|R_{(3,h)}(x)|\le\frac{h^4}{4!\times4^{^2}}\times\underset{a\le x\le b}{max}|f^{(4)}(\xi)| \]
二、均差与差分
(Ⅰ)均差的性质
● 均差性质(1): \(k\)阶均差可表示为函数值\(f(x_0)\)、\(f(x_1)\)、……\(f(x_k)\)。
\[f[x_0,x_1,……x_k]=\sum_{j=0}^k\frac{f(x_j)}{(x_j-x_0)…(x_j-x_{j-1})(x_j-x_{j+1})…(x_j-x_k)} \]
● **均差性质(2): **第\(k\)阶均差可以用如下两个\(k-1\)阶均差表示(均差表的基础)
\[f[x_0,x_1,……x_k]=\frac{f[x_1,……x_k]-f[x_0,x_1,……x_{k-1}]}{x_k-x_0} \]
● 均差性质(3): \(n\)阶均差与导数的关系(分析误差限和牛顿插值函数的精度)
\[f[x_0,x_1,……x_n]=\frac{f^{(n)}(\xi)}{n!},\xi\in[a,b] \]从上述式子中我们就可以看出,牛顿插值的余项为\(f[x,x_0,x_1,……x_n]=\frac{f^{(n+1)}(\xi)}{{n+1}!}\),故精度即为\(n\)。
通常在做题的过程中,性质(1)和性质(3)用得多一些。
(Ⅱ)差分、导数和均差的三角恋
(1)差分与均差的关系:
\[f[x_k,……,x_{k+m}]=\frac{1}{m}\frac{1}{h^m}\Delta^mf_k,其中m=1,2,...,n \]
(2)差分与导数的关系:
\[\Delta^nf_k = h^nf^{(n)}(\xi),其中\xi \in [x_k, x_{k+n}] \]
(3)\(n\)阶均差与导数的关系:
\[f[x_0,x_1,……x_n]=\frac{f^{(n)}(\xi)}{n!},\xi\in[a,b] \]
(Ⅲ)例题
例题1(参考《数值分析 第五版》\(P_{48} T_{8}\))均差与导数的关系\(\Longrightarrow\)牛顿插值函数的精度
题目: \(f(x)=x^7+x^4+3x+1\),求\(f[2^0,2^1,…2^7]\)及\(f[2^0,2^1,…2^8]\)。
解答:
根据\(n\)阶均差与导数的关系:\(f[x_0,x_1,……x_n]=\frac{f^{(n)}(\xi)}{n!}\),我们不难得出:
\[f[x_0,x_1,……x_7]=\frac{f^{(7)}(\xi)}{7!} \qquad \xi\in[2^0,2^7]\\f[x_0,x_1,……x_8]=\frac{f^{(8)}(\eta)}{8!} \qquad \eta\in[2^0,2^8] \]而\(f(x)\)的最高次数为7,所以可得:
\[f[x_0,x_1,……x_7]=\frac{7!}{7!}=1\\f[x_0,x_1,……x_8]=\frac{0}{7!}=0\\ \]
例题2(参考《数值分析 第五版》\(P_{49} T_{12}\))均差与导数的关系\(\Longrightarrow\)牛顿插值函数的精度
题目: \(f(x)=a_0+a_1x+…+a_{n-1}x^{n-1}+a^nx^n\),有\(n\)个不同实根\(x_1,x_2,…,x_n\),证明:
\[\sum_{j=1}^n\frac{x_j^k}{f^{'}(x_j)}=\begin{cases}0,\qquad 0\le k\le n-2;\\\\a_n^{-1},\quad k=n-1;\end{cases} \]解答:
记\(g(x)=x^k\),\(\omega_n(x)=\prod_{i=1}^n(x-x_i)\),则有:
\[f(x)=a_n\cdot\omega_n(x),\qquad f^{'}(x_j)=a_n\omega_n^{'}(x_j) \]由均差的性质(1)可得:\(g[x_1,…x_k]=\sum_{j=0}^k\frac{f(x_j)}{\omega_k^{'}(x_j)}\),又有均差与导数的关系:\(g[x_1,……x_k]=\frac{g^{(k-1)}(\xi)}{{(k-1)}!}\)。
所以有:
\[\sum_{j=1}^n\frac{x_j^k}{f^{'}(x_j)}=\sum_{j=1}^n\frac{x_j^k}{a_n\omega_n^{'}(x_j)}=\frac{1}{a_n}\cdot\sum_{j=1}^n\frac{x_j^k}{\omega_n^{'}(x_j)}=\frac{1}{a_n}\cdot g[x_1,……x_n]=\frac{1}{a_n}\cdot\frac{g^{(n-1)}(\xi)}{{(n-1)}!} \]所以当\(0\le k\le n-2\)时,\(g(x)\)的最高次数为\(k\),对\(g(x)\)求\(n-1\)阶导之后显然为0;
当\(k=n-1\),\(g(x)=x^{n-1}\),所以对\(g(x)\)求\(n-1\)阶导之后为\((n-1)!\),所以得出最后的值为\(a_n^{-1}\);
证毕。