JavaScript--数据结构与算法(三)
数据结构
- 栈
- 队列
- 链表
- 矩阵
- 二叉树
- 堆
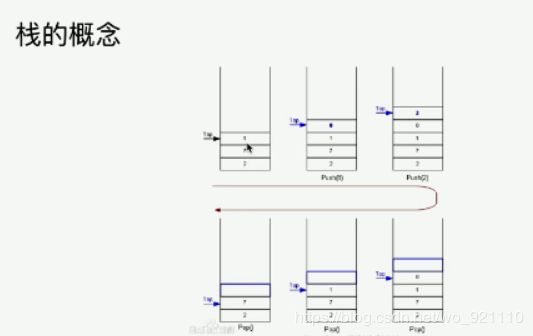
栈
它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表;先进后出的特点
- 棒球比赛
知识点:
利用栈的特点,先进后出来实现这个题目的功能
代码实现:
export default (arr) => {
// 用数组来实现堆栈结构
let result = []
// 上一轮的数据
let pre1
// 上上轮的数据
let pre2
// 对数组进行遍历,遍历的目的是处理得分
arr.forEach(item => {
switch (item) {
case 'C':
if (result.length) {
result.pop()
}
break
case 'D':
pre1 = result.pop()
result.push(pre1, pre1 *2)
break
case '+':
pre1 = result.pop()
pre2 = result.pop()
result.push(pre2, pre1, pre1 + pre2)
break
default:
result.push(item * 1)
}
})
return result.reduce((total, num) => { return total + num })
}- 最大矩阵
图解:
代码实现:
export default (arr) => {
let result = []
let reg = /1{2,}/g
// 把二位数组重新表达,把相邻的1提取出来(起始点 + 截至点)
arr = arr.map(item => {
let str = item.join('')
let r = reg.exec(str)
let rs = []
while (r) {
rs.push([r.index, r.index + r[0].length - 1])
r = reg.exec(str)
}
return rs
})
// 通过递归计算相邻的矩阵
let maxRect = (arr, result, n = 1) => {
// 弹出第一行
let top = arr.pop()
// 弹出第二行
let next = arr.pop()
// 记录第一行的每一个起始点和截至点
let tt
// 记录第二行的每一个起始点和截至点
let nn
// 记录交叉的起始索引
let start
// 记录交叉的截至索引
let end
let width = 1
let maxWidth = 1
n++
for (let i = 0, il = top.length; i < il; i++) {
tt = top[i]
for (let j = 0, jl = next.length; j < jl; j++) {
nn = next[j]
width = Math.min(tt[1], nn[1]) - Math.max(tt[0], nn[0])
if (width > maxWidth) {
maxWidth = width
start = Math.max(tt[0], nn[0])
end = Math.min(tt[1], nn[1])
}
}
}
// 如果没有找到交叉点
if (start === undefined || end === undefined) {
if (n < 3) {
return false
} else {
width = top[0][1] - top[0][0] + 1
if (width > 1) {
result.push((n - 1) * width)
}
}
} else {
arr.push([[start, end]])
maxRect(arr, result, n++)
}
}
while (arr.length > 1) {
maxRect([].concat(arr), result)
arr.pop()
}
// 取最大值
let max = 0
let item = result.pop()
while (item) {
if (item > max) {
max = item
}
item = result.pop()
}
return max > 0 ? max : -1
}
队列
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头;先进先出
- 设计循环队列
export default class MyCircularQueue {
constructor (k) {
// 用来保存数据长度为k的数据结构
this.list = Array(k)
// 队首指针
this.front = 0
// 队尾的指针
this.rear = 0
// 队列的长度
this.max = k
}
// 可以插入返回true,否则返回false
enQueue (num) {
if (this.isFull()) {
return false
} else {
this.list[this.rear] = num
// 实现循环尾指针
this.rear = (this.rear + 1) % this.max
return true
}
}
// 可以删除一个元素返回true否则false
deQueue () {
let v = this.list[this.front]
this.list[this.front] = ''
this.front = (this.front + 1) % this.max
return v
}
isEmpty () {
return this.front === this.rear && !this.list[this.front]
}
isFull () {
return this.front === this.rear && !!this.list[this.front]
}
Front () {
return this.list[this.front]
}
Rear () {
let rear = this.rear - 1
return this.list[rear < 0 ? this.max - 1 : rear]
}
}
- 任务队列
代码实现:
export default (tasks, n) => {
// 表示最终队列执行的结果
let q = ''
// 对归类进行存储
let Q = {}
tasks.forEach(item => {
if (Q[item]) {
Q[item]++
} else {
Q[item] = 1
}
})
while (1) {
// 任务清单
let keys = Object.keys(Q)
if (!keys[0]) {
break
}
// 声明一个队列用来存储1+n任务单元
let tmp = []
for (let i = 0; i <= n; i++) {
let max = 0
let key
let pos
// 找到任务种类最多的
keys.forEach((item, idx) => {
if (Q[item] > max) {
max = Q[item]
key = item
pos = idx
}
})
// 判断当前任务是否存在
if (key) {
tmp.push(key)
keys.splice(pos, 1)
Q[key]--
// 如果任务种类数为0就清楚这个任务
if (Q[key] < 1) {
delete Q[key]
}
} else {
break
}
}
q += tmp.join('').padEnd(n + 1, '-')
}
// 边界的处理,最后不要出现冷却时间
q = q.replace(/-+$/g, '')
return q.length
}
链表
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。
- 排序列表
代码实现:
// 声明链表的节点
class Node {
constructor (value) {
this.val = value
this.next = undefined
}
}
// 声明链表的数据结构
class NodeList {
constructor (arr) {
// 声明链表的头部节点
let head = new Node(arr.shift())
let next = head
arr.forEach(item => {
next.next = new Node(item)
next = next.next
})
// 如果constructor构造实例返回一个对象,这个类就是这个对象
return head
}
}
// 交换两个节点的值
let swap = (p, q) => {
let val = p.val
p.val = q.val
q.val = val
}
// 寻找基准元素的节点
let partion = (begin, end) => {
let val = begin.val
let p = begin
let q = begin.next
while (q !== end) {
if (q.val < val) {
p = p.next
swap(p, q)
}
q = q.next
}
// 让基准元素跑到中间去
swap(p, begin)
return p
}
export default function sort (begin, end) {
if (begin !== end) {
let part = partion(begin, end)
sort(begin, part)
sort(part.next, end)
}
}
export {
Node,
NodeList
}
- 环形链表
代码实现:
// 声明链表的节点
class Node {
constructor (value) {
this.val = value
this.next = undefined
}
}
// 声明链表的数据结构
class NodeList {
constructor (arr) {
// 声明链表的头部节点
let head = new Node(arr.shift())
let next = head
arr.forEach(item => {
next.next = new Node(item)
next = next.next
})
// 如果constructor构造实例返回一个对象,这个类就是这个对象
return head
}
}
export default function isCircle (head) {
// 慢指针
let slow = head
// 快指针
let fast = head.next
while (1) {
if (!fast || !fast.next) {
return false
} else if (fast === slow || fast.next === slow) {
return true
} else {
slow = slow.next
fast = fast.next.next
}
}
}
export {
Node,
NodeList
}
矩阵
矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中
- 螺旋矩阵
代码实现:
export default (arr) => {
// 处理每一圈的数据遍历过程
let map = (arr, r = []) => {
for (let i = 0, len = arr.length; i < len; i++) {
// 判断是否为第一行
if (i === 0) {
r = r.concat(arr[i])
// 判断是否为第二行
} else if (i === len - 1) {
r = r.concat(arr[i].reverse())
// 当不为第一行和不为最后一行的时候
} else {
r.push(arr[i].pop())
}
}
// 清除第一行
arr.shift()
// 清除最后一行
arr.pop()
// 执行左侧的数据遍历
for (let i = arr.length - 1; i >= 0; i--) {
r.push(arr[i].shift())
}
// 判断是否遍历完没有,如果没有则递归
if (arr.length) {
return map(arr, r)
} else {
return r
}
}
return map(arr, [])
}
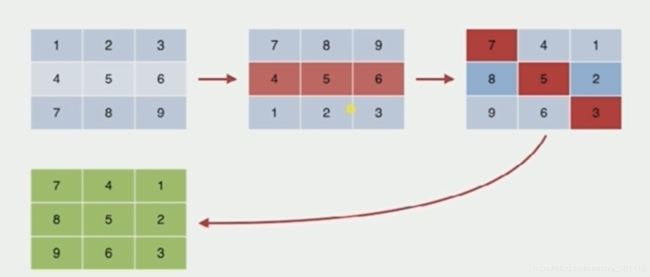
- 螺旋图像
图解:
代码实现:
export default (arr) => {
// 获取n的维度
let vecor = arr.length
// 垂直反转
for (let i = 0, len = vecor / 2; i < len; i++) {
for (let j = 0, tmp; j < vecor; j++) {
tmp = arr[i][j]
arr[i][j] = arr[vecor - i - 1][j]
arr[vecor - i - 1][j] = tmp
}
}
// 对角线反转
for (let i = 0; i < vecor; i++) {
for (let j = 0, tmp; j < i; j++) {
tmp = arr[i][j]
arr[i][j] = arr[j][i]
arr[j][i] = tmp
}
}
return arr
}
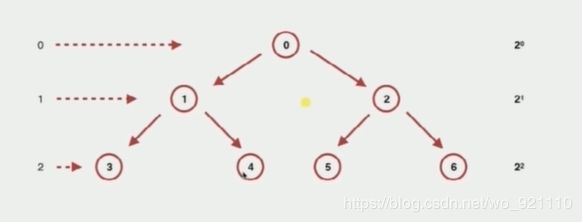
二叉树
学习内容:从零实现一个二叉树的数据结构、围绕二叉树进行基本的操作、
- 对称二叉树
图解:
代码实现:
class Node {
constructor (val) {
this.val = val
this.left = this.right = undefined
}
}
// 构建二叉树
class Tree {
constructor (data) {
// 临时存储所有节点,方便寻找父子节点
let nodeList = []
// 顶节点
let root
for (let i = 0, len = data.length; i < len; i++) {
let node = new Node(data[i])
nodeList.push(node)
if (i > 0) {
// 计算当前节点属于那一层
let n = Math.floor(Math.sqrt(i + 1))
// 记录当前层的起始点
let q = Math.pow(2, n) - 1
// 记录上一层的起始点
let p = Math.pow(2, n - 1) - 1
// 找到当前节点的父节点
let parent = nodeList[p + Math.floor((i - q) / 2)]
// 将当前节点和上一层的父节点做关联
if (parent.left) {
parent.right = node
} else {
parent.left = node
}
}
}
root = nodeList.shift()
nodeList.length = 0
return root
}
// 判断当前二叉树是否为对称的
static isSymmetry (root) {
if (!root) {
return true
}
let walk = (left, right) => {
if (!left && !right) {
return true
}
if ((left && !right) || (!left && right) || (left.val !== right.val)) {
return false
}
return walk(left.left, right.right) && walk(left.right, right.left)
}
return walk(root.left, root.right)
}
}
export default Tree
export {
Node
}
- 验证二叉搜索树
参考文档:Javascript实现二叉树算法
代码的实现:
class Node {
constructor (val) {
this.val = val
this.left = this.right = undefined
}
}
class Tree {
constructor (data) {
let root = new Node(data.shift())
// 遍历所有的数据,逐渐插入到当前这颗搜索树中去
data.forEach(item => {
this.insert(root, item)
})
return root
}
insert (node, data) {
if (data < node.val) {
if (node.left === undefined) {
node.left = new Node(data)
} else {
this.insert(node.left, data)
}
} else {
if (node.right === undefined) {
node.right = new Node(data)
} else {
this.insert(node.right, data)
}
}
}
// 判断当前树是否为搜索二叉树
static walk (root) {
if (!root.left && !root.right) {
return true
} else if ((root.left && root.val < root.left.val) || (root.right && root.val > root.right.val)) {
return false
} else {
return Tree.walk(root.left) && Tree.walk(root.right)
}
}
}
export default Tree
export {
Node
}
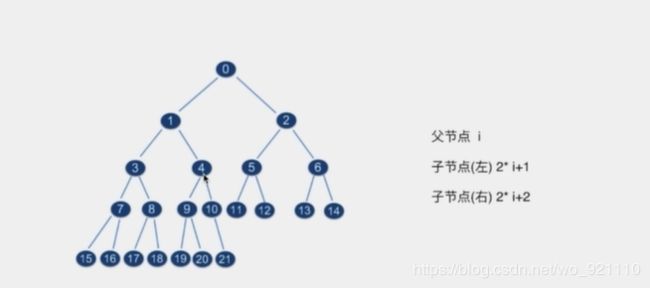
堆
必须是完全二叉树,任一节点的值是其子树所有节点的最大值或最小值
学习内容:堆数据结构的排序、堆数据结构的查找
- 根据字符出现频率排序
图解:
代码实现:
class Heap {
constructor (str) {
let map = new Map()
str.split('').forEach(item => {
if (map.has(item)) {
map.set(item, map.get(item) + 1)
} else {
map.set(item, 1)
}
})
this.map = map
this.data = Array.from(map.values())
}
sort () {
let iArr = this.data
let n = iArr.length
if (n <= 1) {
return iArr
} else {
for (let i = Math.floor(n / 2); i >= 0; i--) {
Heap.maxHeapify(iArr, i, n)
}
for (let j = 0; j < n; j++) {
Heap.swap(iArr, 0, n - 1 - j)
Heap.maxHeapify(iArr, 0, n - 1 - j - 1)
}
return iArr
}
}
toString () {
let arr = this.sort()
let str = []
while (arr.length) {
let top = arr.pop()
for (let [k, v] of this.map) {
if (v === top) {
str.push(k.repeat(v))
this.map.delete(k)
break
}
}
}
return str.join('')
}
// 交换两个元素
static swap (arr, a, b) {
if (a === b) {
return ''
}
let c = arr[a]
arr[a] = arr[b]
arr[b] = c
}
static maxHeapify (Arr, i, size) {
// 左节点(索引)
let l = i * 2 + 1
// 右节点
let r = i * 2 + 2
let largest = i
// 父节点i和左节点l做比较取最大值
if (l <= size && Arr[l] > Arr[largest]) {
largest = l
}
// 右节点和最大值做比较
if (r <= size && Arr[r] > Arr[largest]) {
largest = r
}
if (largest !== i) {
Heap.swap(Arr, i, largest)
Heap.maxHeapify(Arr, largest, size)
}
}
}
export default Heap