全网首发,用到的去B站搜【蓝火小寒冰】点个关注支持一下
功能表:
public class LFSR {
private int state;
private String structConst;
private int n;
public LFSR(int state, String structConst) {
this.state = state;
this.structConst = structConst;
this.n = structConst.length();
drawState();
}
public int getState() {
return state;
}
private int go() {
int out = state;
out >>= n-1;
int in = 0;
for(int i = 0; i < n; i++){
if(structConst.charAt(i) == '1') {
in = in^((state>>i)%2);
}
}
state <<= 1;
state %= 1 << n;
state += in;
return out;
}
public void drawState(){
System.out.print("状态图:");
int[] states = new int[1<>n-j-1) % 2;
System.out.print(out);
}
System.out.print("→");
}
System.out.println("接开头循环");
}
}
public class Exam20200622 {
public static int modInverse(int d, int n){
int a, b, q, r, u=0, v=1, t;
a = n;
b = (d>=0) ? (d%n) : -(d%n);
while(b != 0){
q = a / b;
r = a - b * q;
a = b;
b = r;
t = v;
v = u - q * v;
u = t;
}
if(a != 1)return -a;
else return (u<0) ? u+n : u;
}
public static int modInverseShow(int d, int n){
System.out.println("*************************************************************************");
System.out.println("****NOTICE:[\"\\\" area should be replaced by blank so there is nothing]****");
System.out.println("*************************************************************************");
int up = n;
int down = d;
int inverseUp = 0;
int inverse = 1;
int times, temp;
System.out.println("\\\t\tu\t\tv\t\tq");
System.out.println(up + "\t\t1\t\t0\t\t\\");
System.out.print(down + "\t\t0\t\t1\t\t");
for(;;) {
times = up / down;
System.out.println(times);
temp = up - down * times;
up = down;
down = temp;
temp = inverseUp - inverse * times;
inverseUp = inverse;
inverse = temp;
System.out.print(down + "\t\t\\\t\t" + inverse + "\t\t");
if(down == 1)return (inverse > 0) ? inverse : (inverse + n);
if(down <= 0)return -1;
}
}
public static int modPowerShow(int a, int k, int n){
System.out.println("*************************************************************************");
System.out.println("****NOTICE:[\"\\\" area should be replaced by blank so there is nothing]****");
System.out.println("****NOTICE:[\"(3=))\" area should be replaced by three line equal]*********");
System.out.println("*************************************************************************");
System.out.println("i\t\tki\t\tx\t\ty");
int now, x = 1, y = a, power;
for(int i = 0;;i++){
now = k % 2;
System.out.print(i + "\t\t" + now + "\t\t");
power = (x * y) % n;
if(now == 1) {
System.out.print(x + "x" + y + "(3=)" + power + "\t\t");
x = power;
}
else System.out.print(x + "\t\t");
y = (y * y) % n;
System.out.println(a + "^(2^" + (i+1) + ")" + "(3=)" + y);
k /= 2;
if(k == 1)break;
}
power = (x * y) % n;
System.out.println("\\\t\t\\\t\t" + x + "x" + y + "(3=)" + power);
return power;
}
public static String xTimeShow(String data, String times){
System.out.println("************************************************************");
System.out.println("****NOTICE:[Copy lines form second to the last you used]****");
System.out.println("************************************************************");
int tar = hex2Dec(data);
int n = hex2Dec(times);
int answer = 0;
for(int i = 0; i < 8; i++){
if(n%(int)Math.pow(2,i+1) == (int)Math.pow(2,i)){
answer ^= tar;
n -= (int)Math.pow(2,i);
}
System.out.println(data + "x" + dec2Hex((int)Math.pow(2,i)) + "=" + dec2Hex(tar));
tar *= 2;
if(tar >= 256){
tar -= 256;
tar ^= 27;
}
}
System.out.println(data + "x" + times + "= ... = ... =" + dec2Hex(answer));
return dec2Hex(answer);
}
private static int hex2Dec(String hex){
hex = hex.toLowerCase();
int dec = 0;
for(int i = 0; i < hex.length(); i++){
char letter = hex.charAt(i);
if(letter >= 48 && letter <= 57)dec += (letter - 48) * Math.pow(16,hex.length() - i - 1);
else dec += (letter - 87) * Math.pow(16,hex.length() - i - 1);
}
return dec;
}
private static String dec2Hex(int dec){
String hex = "";
int[] num = new int[2];
num[0] = (dec % 256) / 16;
num[1] = dec % 16;
if(num[0] >= 0 && num[0] <= 9)hex += num[0];
else hex += (char)(num[0] + 87);
if(num[1] >= 0 && num[1] <= 9)hex += num[1];
else hex += (char)(num[1] + 87);
return hex;
}
public static int[] ECCADD(int a, int p, int xp, int yp, int xq, int yq){
if(xq == 0 && yq == 0){
System.out.println("(" + xp + "," + yp + ")");
return new int[]{xp,yp};
}
if(xp == 0 && yp == 0){
System.out.println("(" + xq + "," + yq + ")");
return new int[]{xq,yq};
}
if(xp == xq && (yp + yq) % p == 0){
System.out.println("O (0,0)");
return new int[]{0,0};
}
int lamb;
if(xp == xq && yp == yq){
lamb = ((3 * xp * xp + a) * modInverse(2*yp,p)) % p;
}
else {
lamb = ((yq - yp) * modInverse(xq-xp,p)) % p;
}
if(lamb < 0) lamb += p;
System.out.print("lamb = " + lamb);
int x = (lamb * lamb - xp - xq) % p;
if(x < 0) x += p;
int y = (lamb * (xp-x) - yp) % p;
if(y < 0) y += p;
System.out.println(" newPoint = (" + x + "," + y + ")");
return new int[]{x,y};
}
public static int[] ECCMUL(int a, int p, int times, int xp, int yp){
int[] answer = new int[]{xp,yp};
for(int i = 0; i < times - 1; i++){
System.out.print((i+2)+"G\t");
answer = ECCADD(a,p,xp,yp,answer[0],answer[1]);
}
return answer;
}
public static int[][] getECCPoint(int a, int b, int p){
int[][] point = new int[p+1+(int)(2*Math.sqrt(p))][2];
point[0] = new int[]{0,0};
System.out.print("(0,0)");
int index = 1;
int[] y2should = new int[p];
for(int i = 0; i < p; i++){
y2should[i] = (i*i*i + a * i + b) % p;
}
int[] y2real = new int[p];
for(int i = 0; i < p; i++){
y2real[i] = (i*i) % p;
}
for(int i = 0; i < p; i++){
for(int j = 0; j < p; j++){
if(y2should[i] == y2real[j]){
point[index][0] = i;
point[index][1] = j;
System.out.print((",(" + i + "," + j + ")"));
index++;
}
}
}
System.out.println();
return point;
}
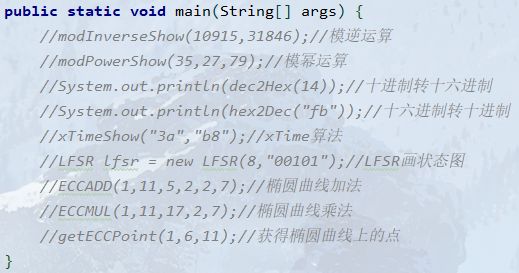
public static void main(String[] args) {
//modInverseShow(10915,31846);//模逆运算
//modPowerShow(35,27,79);//模幂运算
//System.out.println(dec2Hex(14));//十进制转十六进制
//System.out.println(hex2Dec("fb"));//十六进制转十进制
//xTimeShow("3a","b8");//xTime算法
//LFSR lfsr = new LFSR(8,"00101");//LFSR画状态图
//ECCADD(1,11,5,2,2,7);//椭圆曲线加法
//ECCMUL(1,11,17,2,7);//椭圆曲线乘法
//getECCPoint(1,6,11);//获得椭圆曲线上的点
}
}
