数据结构之图---最小生成树Kruskal算法---C++实现
一.需求图Kruskal算法最小生成树
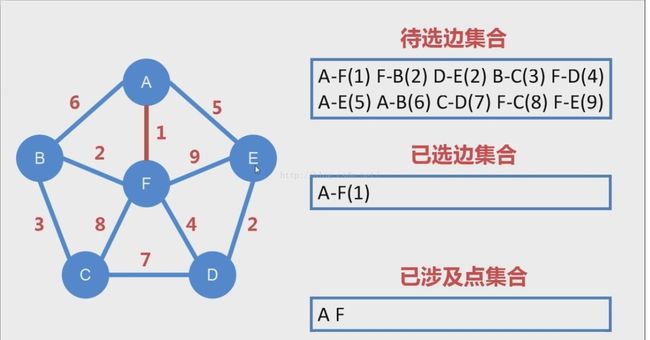
无向图中点与点之间,边上的数字表示权值。
二.实现Kruskal算法最小生成树
1.边的描述
定义边的对象时应有以下属性:这条边连接两端的点(nodeIndexA,nodeIndexB),边的权值,以及这条边是否被选中
2.图的描述
上述1,2与Prim算法一致见:3.Kruskal算法代码
//在CMap.cpp中添加
void CMap::kruskalTree() //克鲁斯卡尔算法最小生成树
{
int value = 0;
int edgeCount = 0;
//定义存放结点集合的数组
vector> nodeSets;
//第一步:取出所有边
vector edgeVec;
for (int i = 0; i < m_iCapacity; i++) //取邻接矩阵上半三角不含对角线的顶点
{
for (int k = i + 1; k < m_iCapacity; k++)
{
getValueFromMatrix(i, k, value);
if (value != 0)
{
Edge edge(i, k, value); //边的实例化
edgeVec.push_back(edge);
}
}
}
//克鲁斯卡尔算法最小生成树
/*第二步:从所有边中取出组成最小生成树的边*/
//1.找到算法结束的条件
//while (edgeCount < m_iCapacity -1)
for (; edgeCount < m_iCapacity - 1;edgeCount++)
{
//2.从边集合中找到最小边
int minEdgeIndex = getMinEdge(edgeVec);
edgeVec[minEdgeIndex].m_bSelected = true;
//3.找出最小边连接的点
int nodeAIndex = edgeVec[minEdgeIndex].m_iNodeIndexA;
int nodeBIndex = edgeVec[minEdgeIndex].m_iNodeIndexB;
//4.找出点所在的点集合
bool nodeAIsInSet = false;
bool nodeBIsInSet = false;
int nodeAInSetLabel = -1;
int nodeBInSetLabel = -1;
for (int i = 0; i < (int)nodeSets.size();i++)
{
nodeAIsInSet = isInSet(nodeSets[i],nodeAIndex); //检查边的A点是否在结点集合中
if (nodeAIsInSet)
{
nodeAInSetLabel = i;
}
}
for (int i = 0; i < (int)nodeSets.size(); i++)
{
nodeBIsInSet = isInSet(nodeSets[i], nodeBIndex); ////检查边的B点是否在结点集合中
if (nodeBIsInSet)
{
nodeBInSetLabel = i;
}
}
//5.根据点所在集合的不同做出不同的处理
if (nodeAInSetLabel == -1 && nodeBInSetLabel == -1)
{
vector vec;
vec.push_back(nodeAIndex);
vec.push_back(nodeBIndex);
nodeSets.push_back(vec);
}
else if (nodeAInSetLabel == -1 && nodeBInSetLabel != 1)
{
nodeSets[nodeBInSetLabel].push_back(nodeAIndex);
}
else if (nodeAInSetLabel != -1 && nodeBInSetLabel == 1)
{
nodeSets[nodeAInSetLabel].push_back(nodeBIndex);
}
else if (nodeAInSetLabel != -1 && nodeBInSetLabel != -1 && nodeAInSetLabel != nodeBInSetLabel)
{
mergeNodeSet(nodeSets[nodeAInSetLabel], nodeSets[nodeBInSetLabel]);
for (int k = nodeBInSetLabel; k<(int)nodeSets.size()-1;k++)
{
nodeSets[k] = nodeSets[k + 1];
}
}
else if (nodeAInSetLabel != -1 && nodeBInSetLabel != -1 && nodeAInSetLabel == nodeBInSetLabel)
{
continue; //形成回路
}
m_pEdge[edgeCount] = edgeVec[minEdgeIndex];
//edgeCount++;
cout << edgeVec[minEdgeIndex].m_iNodeIndexA << "----" << edgeVec[minEdgeIndex].m_iNodeIndexB << " " << edgeVec[minEdgeIndex].m_iWeightValue << endl;
}
}
bool CMap::isInSet(vector nodeSet, int target)
{
for (int i = 0; i < (int)nodeSet.size();i++)
{
if (nodeSet[i]==target)
{
return true;
}
}
return false;
}
void CMap::mergeNodeSet(vector &nodeSetA, vector nodeSetB)
{
for (int i = 0; i < (int)nodeSetB.size();i++)
{
nodeSetA.push_back(nodeSetB[i]);
}
}
//中main.cpp中添加
pMap->kruskalTree();
三.Kruskal算法的分析
1.Krusual算法和Prim算法不同之处在于,调用Krusual算法不需要传入结点的索引。即一开始是和结点无关的
2.遍历邻接矩阵,取出整个图的所有边,放入待选边集合中edgeVec,该集合中边的对象含有这条边连接的两个结点(nodeIndexA,nodeIndexB),权值(weightValue)
3.Kruskal算法是实现最小生成树,算法结束的条件是edgeCount < m_iCapacity -1。
4.从待选边集合中取出权值最小的一条边A-F(1),并将边的Selected属性置true(保证只出现一次)。
5.找出与权值最小边相连接的结点nodeAIndex,nodeBIndex,其实此时也就是A点和F点。
6.找出A点和F点所在的点集合。因为此时点集合为空,直接进入下一步。
7.根据点所在集合的不同做出不同的处理。此时A和F还不属于任何一个集合,属于情况1,直接将A和F放入点集合nodeSets[0]中.
////////////////////////////////////////////////////////////////////////////////////////////////////////////8.继续从待选边集合中edgeVec取出第二小的边B-F(2),并将边的Selected属性置true(保证只出现一次)。
9.找出与权值最小边相连接的结点nodeAIndex,nodeBIndex,其实此时也就是B点和F点。
10.找出B点和F点所在的点集合。
此时点集合中nodeSets[0]中有两个元素(A,F),
找F是否在点集合nodeSets[0]中,如果在就将点集合的所在的索引赋值给nodeBInSetLabel = 0。
找B是否在点集合nodeSets[0]中,如果不在nodeAInSetLabel 保持为false
11.根据点所在集合的不同做出不同的处理。
此时B不在集合中,F在集合中,属于情况2,将B点放入点集合nodeSets[0]中。
////////////////////////////////////////////////////////////////////////////////////////////////////////////12.继续从待选边集合中edgeVec取出第三小的边D-E(2),并将边的Selected属性置true(保证只出现一次)。
13.找出与权值最小边相连接的结点nodeAIndex,nodeBIndex,其实此时也就是D点和E点。
14.找出D点和E点所在的点集合。
此时点集合中nodeSets[0]中有三个元素(A,F,B),
找D是否在点集合nodeSets[0]中,如果不在nodeAInSetLabel 保持为false
找E是否在点集合nodeSets[0]中,如果不在nodeBInSetLabel 保持为false
15.根据点所在集合的不同做出不同的处理。
此时D不在集合中,E不在集合中,属于情况1,直接将D和E放入点集合nodeSets[1]中.
////////////////////////////////////////////////////////////////////////////////////////////////////////////16.继续从待选边集合中edgeVec取出第四小的边B-C(3),类似8---11,之后点集合nodeSets[0]的元素有A,F,B,C
////////////////////////////////////////////////////////////////////////////////////////////////////////////
17.继续从待选边集合中edgeVec取出第五小的边D-F(4),并将边的Selected属性置true(保证只出现一次)。
18.找出与权值最小边相连接的结点nodeAIndex,nodeBIndex,其实此时也就是D点和F点。
19.找出D点和F点所在的点集合。
此时点集合中nodeSets[0]中有三个元素(A,F,B,C),
找D是否在点集合nodeSets[0]中,如果不在nodeAInSetLabel 保持为false
找F是否在点集合nodeSets[0]中,如果在就将点集合的所在的索引赋值给nodeBInSetLabel = 0。
此时点集合中nodeSets[1]中有三个元素(D,E),
找D是否在点集合nodeSets[1]中,如果在就将点集合的所在的索引赋值给nodeAInSetLabel = 1。
找F是否在点集合nodeSets[1]中,如果不在nodeBInSetLabel 保持为nodeBInSetLabel = 0。
20.根据点所在集合的不同做出不同的处理。
此时D在nodeSets[1]集合中,F在nodeSets[0]集合中,属于情况4,将两个集合.融合放入到集合nodeSets[0]中,共有A,F,B,C,D,E元素。
有6个顶点,最小生成树的边=6-1=5,结束循环。