Timed-Elastic-Band局部路径规划算法
早前做工程时尝试了teb局部规划算法,觉得效果非常好。由于时间关系,并未深入了解,仅依靠做对比实验调节作者给出的接口参数满足工程需求。抽空看了一下作者关于teb算法的论文,记录一些笔记。
teb局部路径规划算法github地址:https://github.com/rst-tu-dortmund/teb_local_planner。
作者列出的几篇文章均推荐阅读了解。本文基于《Trajectory modification considering dynamic constraints of autonomous robots》一文。
关于time eletic band这个概念,在这推荐看一下qqfly的文章,非常生动形象:link
qqfly文章中关于eletic band(橡皮筋)的定义:连接起始、目标点,并让这个路径可以变形,变形的条件就是将所有约束当做橡皮筋的外力。关于time eletic band的简述:起始点、目标点状态由用户/全局规划器指定,中间插入N个控制橡皮筋形状的控制点(机器人姿态),当然,为了显示轨迹的运动学信息,我们在点与点之间定义运动时间Time,即为Timed-Elastic-Band算法。
以下为《Trajectory modification considering dynamic constraints of autonomous robots》的阅读笔记。
默认的环境为二维差动轮机器人。
一、Timed Elastic Band概述
定义机器人位姿:
![]() ;
;
其中![]() ,
,![]() 和
和![]() 分别对应机器人在map坐标系(或者世界坐标系)的位置和姿态,文章中称其为configuration。
分别对应机器人在map坐标系(或者世界坐标系)的位置和姿态,文章中称其为configuration。
则空间内configuration序列(如figure 1)记录如下:
![]() (1)
(1)
两个configuration间的时间间隔定义为:![]() ,表示机器人由一个configuration运动到另一个configuration所需时间;
,表示机器人由一个configuration运动到另一个configuration所需时间;
记录时间序列:
![]() (2)
(2)
将configuration及时间序列合并:
![]() (3)
(3)
通过加权多目标优化获取最优的路径点,即最优的Q:
![]() (5)
(5)
其中![]() 为最优结果,
为最优结果,![]() 为考虑各种约束的目标函数,
为考虑各种约束的目标函数,![]() 为个目标函数的权值。
为个目标函数的权值。
在此应注意,每个目标函数只与elastic band中的某几个连续状态有关,而非整条band。故优化为对稀疏矩阵模型的优化。具体细节请参考《Efficient trajectory optimization using a sparse model》。
作者在撰写论文时ROS对稀疏矩阵优化问题的支持并未十分完善,故作者采用分段连续,可微分的代价函数计算破坏约束的惩罚值。
(6)
其中![]() 为限界值,
为限界值,![]() 影响近似的准确度。具体地说,
影响近似的准确度。具体地说,![]() 表示缩放,n表示多项式阶数,
表示缩放,n表示多项式阶数,![]() 表示限界值附近一个小位移。
表示限界值附近一个小位移。
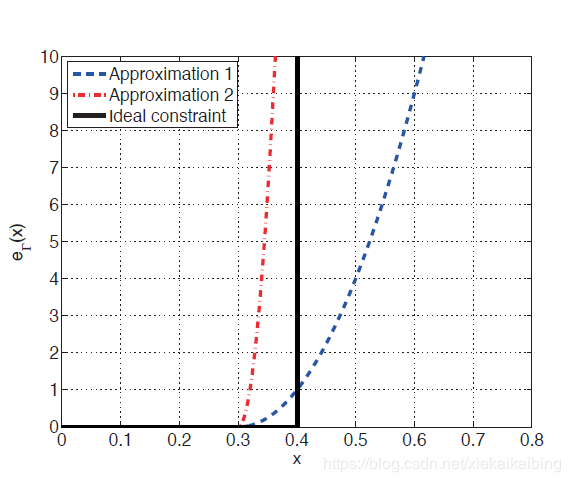
以figure 2为例。限界值![]() ,即不应超过0.4。途中ideal constraint表现为x<0.4时,代价值为0,当x=0.4时惩罚代价值无穷大。Approximation 1的参数为:
,即不应超过0.4。途中ideal constraint表现为x<0.4时,代价值为0,当x=0.4时惩罚代价值无穷大。Approximation 1的参数为:![]() ;Approximation 2的参数为
;Approximation 2的参数为![]() 。两项均从x=0.3开始代价函数惩罚起作用。理论上Approximation 1在x>0.4时函数仍起作用,但Approximation 2能有效防止x越界。
。两项均从x=0.3开始代价函数惩罚起作用。理论上Approximation 1在x>0.4时函数仍起作用,但Approximation 2能有效防止x越界。
二、约束目标函数
1、跟随路径和避障约束
约束主要有两个目标:跟随已知的全局规划路径和避障。两个目标函数均十分相似,跟随路径施力将elastic bands拉向全局路径,而避障约束施力使得elastic bands远离障碍物。configuration序列与全局路径点序列或障碍物![]() 的最近距离记为
的最近距离记为![]() ,如figure 3所示。跟随路径目标以configuration距全局路径的允许最大距离
,如figure 3所示。跟随路径目标以configuration距全局路径的允许最大距离![]() 作为约束,避障目标以configuration距障碍物的允许最小距离
作为约束,避障目标以configuration距障碍物的允许最小距离![]() 作为约束。
作为约束。
实际上原文约束为attainment of the intermediate way points of the original path,是否为我所理解的跟随全局规划路径还有待商榷。
约束以惩罚函数实现:
![]() (7)
(7)
![]() (8)
(8)
值得注意的是,目标函数的梯度可视为对elastic band施加的外力。
2、速度和加速度约束
由速度和加速度组成的动力学约束可以用类似1中运动学约束的惩罚函数表示。以figure 3为例,机器人运动的平均线速度和角速度可以通过相邻的configuration![]() 和时间间隔
和时间间隔![]() 计算得到。
计算得到。
类似的,线速度约束可以表示为:
![]()
机器人的平均线加速度用同样的近似计算得到:
角加速度同理可计算得到。
以差动机器人为运动模型,两轮的转速可通过以下计算得到:
![]() (12)
(12)
![]() (13)
(13)
其中L为两轮轴距的一半。
对(12)(13)式作关于时间的微分得到两轮的加速度。
则可结合机器人设计的机械参数得到的轮子速度和加速度的上下界确定约束上下界。
3、Non-holonomic运动学约束
差动机器人在平面运动只有两个自由度,其只能以朝向的方向直线运动或旋转。这种运动学约束使得机器人以有若干弧段组成的平滑的轨迹运动。相邻的两个configuration应在弧段的两端,如figure 4。
初始configuration![]() 与运动方向
与运动方向![]() 的夹角
的夹角![]() 应与结束configuration对应的夹角
应与结束configuration对应的夹角![]() 相等。
相等。
若![]() 为机器人在第i段弧段相对于世界坐标系的绝对姿态,则有:
为机器人在第i段弧段相对于世界坐标系的绝对姿态,则有:
![]() (14)
(14)
其中,运动方向向量:
相应的目标函数:
(17)
要注意机器人运动在180度附近的越界的情况。
4、最快路径约束
目标函数即为最小化时间间隔序列的二次方。
目标函数使得机器人获得最快路径,路径上的各configuration点在时间上均匀分开,而非传统的空间上求最短路径。
三、teb实现
teb的控制流程如figure 5。
在initialization阶段,通过增加满足运动学和动力学约束默认的时间信息将an initial path添加到an initial trajectory(不太理解)。
每次迭代过程中,算法动态添加新的configuration,删除旧的configuration以将关于空间和时间的分辨率调整至余下的轨迹长度和规划的范围内。添加一个hysteresis实现避障。优化问题转化为一个hyper-graph问题,通过g2o中关于大规模稀疏矩阵的优化算法解决。
teb优化问题(公式4)可以转化为hyper-graph问题。configurations和以及时间间隔作为nodes,目标函数![]() 以及其他约束函数为edges,各nodes由edges连接起来构成hyper-graph。该graph中,每一个约束都为一条edge,并且每条edge允许连接的nodes的数目是不受限制的。
以及其他约束函数为edges,各nodes由edges连接起来构成hyper-graph。该graph中,每一个约束都为一条edge,并且每条edge允许连接的nodes的数目是不受限制的。
图6(a)中展示了两个configurations![]() ,一个时间间隔
,一个时间间隔![]() ,一个障碍点
,一个障碍点![]() 组成的hyper-graph。速度约束需要计算平均速度,则该约束与
组成的hyper-graph。速度约束需要计算平均速度,则该约束与![]() 相关,该edge将三个nodes连接起来。障碍物约束将障碍物和离障碍物最近的configuration连接起来。注意障碍物点是固定的,算法不应也不能对其位置进行优化。
相关,该edge将三个nodes连接起来。障碍物约束将障碍物和离障碍物最近的configuration连接起来。注意障碍物点是固定的,算法不应也不能对其位置进行优化。
图6(b)中则展示了更大的teb hyper-graph。
在确认能进行teb优化后(Verify trajectory),将计算控制量![]() 和
和![]() 直接用于机器人系统。
直接用于机器人系统。
在每次迭代开始前的re-initialization阶段,在分析shortrange camera or laser-scan data后可能会收到新的way points,此时就会check新的和更改后的way points。