拜占庭将军问题(一)—— 引言与结论
拜占庭将军问题(The Byzantine Generals Problem)是Leslie Lamport在其同名的论文1提出的一种针对分布式对等网络中的容错问题。
一个可靠的计算机系统需要能够处理一个或多个系统组件的失效。一个失效的组件可能会表现为发送错误的信息,或者因组件故障不发出信息等行为。这种类型的失效问题被称为拜占庭将军问题。Leslie在这篇论文中对拜占庭将军问题进行了描述并提出解决拜占庭问题的一些方法。
问题描述
Leslie通过几支拜占庭将军领导的军队共同进攻敌方城池的例子描述了这个问题。
假如几支拜占庭将军领导的军队驻扎在敌方城池周围,准备攻城。将军们之间只能通过通信的方式相互沟通。在观察敌情之后,他们需要共同确定行动。但是,其中一些将军可能是叛徒,他们会试图阻止忠诚将军之间达成一致行动。因此,拜占庭将军们需要一种算法来保证:
A. 所有忠诚的将军能采取同样的行动
忠诚的将军会按照算法行动,但叛徒会采取任何行动。因此,算法需要保证无论叛徒干什么,条件A都会被满足。
B. 一小部分的叛徒不会导致忠诚的将军采取错误的行动
条件B是很难形式化的,因为它需要对错误的行动进行准确的描述。因此,Leslie用将军如何作出决定来代替。
“将军-将军”问题 or “司令-副官”问题
令:
n: 将军的数量
***v(i)***: 由第***i***将军发出的消息
每位将军采用某种函数从***(v(1), …, v(n))作出决定。例如,采用***Majority***投票方法,选取(v(1), …, v(n))***多数的行动作为最优的行动。在这种情况下,只有忠诚将军不同行动的数量大致相等,小部分叛徒才能影响忠诚将军的行动。
拜占庭将军之间要想达成一致,最明显的办法是第***i***号将军通过传令兵向其他每个将军发出***v(i)***,但是,由于叛徒可能向不同的将军发出不同的值。如果想要满足条件A,需要满足如下条件:
条件1:每个忠诚的将军必须获得相同的行动指令集合***(v(1), …, v(n))***
如果第**i号将军是叛徒,并向不同的将军发送不同的行动指令,所以条件1也暗含一个将军不一定是从第***i***号将军直接获取**v(i)。这就意味着,如果要满足条件1,需要考虑一个将军使用不是***i***号将军发出的v(i)作为**i号将军的行动指令,即使第i号将军是忠诚的,这与条件B是相矛盾的。例如,不能让一部分叛徒影响忠诚将军基于(“撤退”, …, “撤退”)作出决定,即使每个忠诚将军发出的都是“进攻”。因此,还需要满足下面的条件:
条件2:如果第***i***号将军是忠诚的,那么每个忠诚将军必须用第***i***号将军发出的行动指令作为***v(i)***
接下来,针对每个i***,对条件1*进行重写:
条件 1 ′ 1' 1′:任意两个忠诚的将军使用相同的***v(i)***
条件 1 ′ 1' 1′和条件2都是针对第***i***号将军发出的行动指令的条件。因此,可以将拜占庭将军问题归结为一个将军如何发送他的值给其他人,即一个司令官发送命令给他的副官问题,如下:
拜占庭将军问题: 一个司令官发送命令给他的***n-1***个副官,需满足条件:
IC1. 所有忠诚副官遵守同一命令;
IC2. 如果司令官是忠诚的,每个忠诚的副官遵守他的命令。
条件IC1和IC2被称为交互一致性条件(interactive consistency conditions)。为了解决原来的问题,第***i***号将军作为将军,采用拜占庭将军问题的解决方法,发送他的行动指令***v(i)***,其他将军作为副官进行行动。
不可能的结果
拜占庭将军问题看起来是简单的,但如果在每个将军只传输口头消息(oral messages)的情况下,只有忠诚的将军数量多于2/3,拜占庭将军问题才有解。口头消息指的是发出的消息完全由发送者控制,这就意味着叛徒可以发送任意消息。还有一种是将军之间传输签名的书面消息,在这种情况下,结论又是不一样的。
例证
首先,Leslie论述了在传输口头消息的情况下,三个将军中有一个是叛徒时,拜占庭将军问题是无解的。为了简化论述,将军可做的行动只有“进攻”和“撤退”两种。下面分两种情况进行讨论:
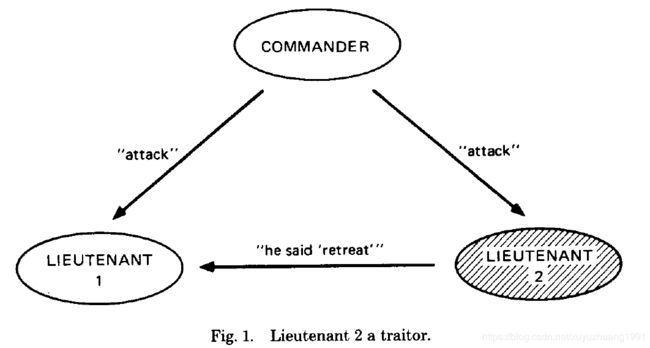
- 假如司令是忠诚的
令副官1是忠诚的,副官2是叛徒,如Fig 1。假如司令发出的是“进攻”命令,副官2会向副官1发送错误信息——“我收到的是撤退”。由于副官1是忠诚的,如果想满足条件IC2,副官1会执行进攻命令。
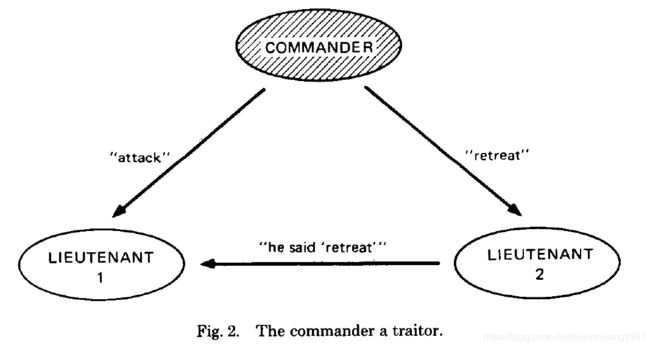
- 假如司令是叛徒
副官1和副官2都是忠诚的,如Fig 2。司令向副官1发送“进攻”指令,司令向副官2发送“撤退”指令。副官2如实告诉副官1——“我收到的是撤退命令”。由于副官1分辨不出谁是叛徒,所以他判断不出司令发给副官2的真实命令是什么,那么他只能遵从司令执行“进攻”。同样地,副官2也会遵从司令执行“撤退”命令,此时就违背了条件IC1。
通过上面的例子虽然可以证明在三个将军中有一个叛徒的情况下,拜占庭将军问题是无解的。但还需要更严格的形式化证明,有兴趣的读者可以参考文献22。
一般性推论
利用上面的结果,可以用反证法证明少于3m+1个将军中有m个叛徒的情况是无解的。
思路: 假设存在一个解,使得3m或更少的将军数量能够处理m个叛徒,那么用此来构建一个三将军拜占庭将军问题的解,这个结论在上一节中证明是不可能的。
为了避免混淆,令假设的解中的将军为阿尔巴尼亚将军(Albanian Generals),真实情况下的将军还是称为拜占庭将军。假设3m个或更少的阿尔巴尼亚将军能够处理m个叛徒的情况,下面我们来构建“三”拜占庭将军问题的解。
令“三”拜占庭将军问题中的每个将军模拟大约1/3数量的阿尔巴尼亚将军的行动,即每个拜占庭将军模拟至多m个阿尔巴尼亚将军。也就是说,拜占庭司令官模拟阿尔巴尼亚司令官和至多m-1个阿尔巴尼亚副官,每个拜占庭副官模拟至多m个副官。
由于假设了阿尔巴尼亚将军有解,即其满足条件IC1和IC2。根据IC1,由忠诚的拜占庭将军模拟的阿尔巴尼亚将军则会执行相同的行动,即“三”拜占庭将军也满足IC1,同理,由阿尔巴尼亚将军满足IC2也能推出“三”拜占庭将军也满足IC2,也就为“三”拜占庭将军问题找到了一个解,这与上一节“三”拜占庭将军问题是无解的是相矛盾的。因此,假设不成立,即少于3m+1个将军中有m个叛徒的情况是无解的。
另外,Leslie也证明了拜占庭将军问题的结论和将军们达成的一致行动是不是精确的无关,此处不再论述,感兴趣的读者可以去Leslie的原著。
注:在传输**签名书面消息(Signed Messages)**时,结论是,对于任意数量的将军和可能的叛徒,拜占庭将军问题都是有解的。
小结
本篇文章介绍了Leslie原著的第一、二节:
- 拜占庭将军问题的描述及达成一致的条件;
- 传输口头消息时,少于3m+1个将军中有m个叛徒是无解的。
后续的文章中,对Leslie针对口头消息和签名的书面消息两种情况下构建的算法进行阐述。
Lamport L, Shostak R, Pease M. The Byzantine generals problem[J]. ACM Transactions on Programming Languages and Systems (TOPLAS), 1982, 4(3): 382-401. ↩︎
Pease M, Shostak R, Lamport L. Reaching agreement in the presence of faults[J]. Journal of the ACM (JACM), 1980, 27(2): 228-234. ↩︎