基于Python的逻辑回归实现及数据挖掘应用案例讲解
商业背景:随着三大运营商和民营企业的迅猛发展,移动市场竞争激烈,市场日趋饱和,各通信运营商的发展重心由发展新用户过渡到维系保有老用户,为了更好支撑老用户维系工作,用户流失预警作为其中一项重要环节被尤其重视,本案例是基于电信集团某省公司几千万用户数据展开。
本案例只展示核心步骤及相关代码,使用工具为Python,主要算法和技术为LR、RandomForest、交叉验证法、网格搜索调优参数。
第一步、数据库数据读取
近两千万用户规模,考量时间跨度为3个月,综合用户基本信息、订购数据、套餐数据、财务及缴费数据、通信行为数据、使用终端数据、投诉及维修数据、互联网搜索及DPI数据共106个指标,另外本案例为ORACLE数据库:
# -*- coding: utf-8 -*-
# 某省电信用户流失预警专题
# author: ***
# date: 11-01
# note: 基于Python3.6 编写
#####数据库读取数据##############
import pandas as pd
import cx_Oracle as co
import os
def query(table,column):
username = "用户账号"
pwd = "密码"
dsn = co.makedsn('数据库ID','1521','sdedw')
conn = co.connect(username,pwd,dsn)
cursor = conn.cursor()
sql = table
cursor.execute(sql)
rows = cursor.fetchall()
count = cursor.rowcount
print("=====================")
print("Total:", count)
print("=====================")
data = pd.DataFrame(rows,columns = column)
cursor.close
return data定义指标名称并对数据表重命名,转换成python可以识别的形式,用以后续分析建模,由于原始数据表数据驳杂,质量不高,首先在数据库里进行了初步加工,形成最后的目标表:
data_ls = query("select * from temp_rwk_cnk_ls6_21",['SERV_ID','CUST_AGE','SERV_NEW_CUST_TYPE',……,'IS_LIUSHI'])
data_ls = data_ls.set_index('SERV_ID') #指定索引相关模块加载:
import numpy as np
import datetime
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import seaborn as sns
sns.set_style('whitegrid')
import missingno as msno
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import auc
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
from sklearn.metrics import recall_score
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
from sklearn import metrics
# 忽略弹出的warnings
import warnings
warnings.filterwarnings('ignore')
pd.set_option('display.float_format', lambda x: '%.4f' % x)
from imblearn.over_sampling import SMOTE
import itertools第二步、数据查看及处理
import os
os.chdir('E:\\Python\\model_sd_chaoniuka_ls') # change working directory
data_ls.head()
data_ls.shape
data_ls.info()
data_ls.describe().T
# 目标变量(IS_LIUSHI)分布可视化
fig, axs = plt.subplots(1,2,figsize=(14,7))
sns.countplot(x='IS_LIUSHI',data=data_ls,ax=axs[0])
axs[0].set_title("Frequency of each IS_LIUSHI")
data_ls['IS_LIUSHI'].value_counts().plot(x=None,y=None, kind='pie', ax=axs[1],)
axs[1].set_title("Percentage of each IS_LIUSHI")
plt.show()
# 查看缺失值情况
def na_count(data):
data_count = data.count()
na_count = len(data) - data_count
na_rate = na_count/len(data)
result = pd.concat([data_count,na_count,na_rate],axis = 1)
return result;
na_count(data_ls)
data_ls = data_ls.dropna(how='any') #去掉包含缺失值的行指标相关分析及基于随机森林算法的指标重要性分析:
####### 相关性分析 #######
def data_corr_analysis(data, sigmod):
# 返回出原始数据的相关性矩阵以及根据阈值筛选之后的相关性较高的变量
corr_data = data.corr()
for i in range(len(corr_data)):
for j in range(len(corr_data)):
if j >= i:
corr_data.iloc[i, j] = 0
x, y = [], []
for i in list(corr_data.index):
for j in list(corr_data.columns):
if abs(corr_data.loc[i, j]) >= sigmod:
x.append(i)
y.append(j)
z = [[x[i], y[i]] for i in range(len(x))]
return corr_data, pd.DataFrame(z, columns=['index','columns'])
data_corr_analysis(data_ls, 0.8)
data_ls = data_ls.drop(['CALLING_DURATION','CALLING_DURATION_TREND','CALLING_COUNT'], axis=1)
# 对特征的重要性进行排序:构建X变量和Y变量。
x_feature = list(data_ls.columns)
x_feature.remove('IS_LIUSHI')
x_val = data_ls[x_feature]
y_val = data_ls['IS_LIUSHI']
# 利用随机森林的feature importance对特征的重要性进行排序。
names = data_ls[x_feature].columns
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=10,random_state=123)
clf.fit(x_val, y_val)
names, clf.feature_importances_
for feature in zip(names, clf.feature_importances_):
print(feature)
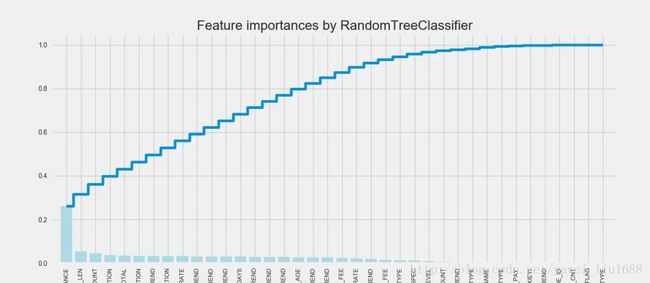
plt.style.use('fivethirtyeight')
plt.rcParams['figure.figsize'] = (12,6)
## feature importances 可视化
importances = clf.feature_importances_
feat_names = names
indices = np.argsort(importances)[::-1]
fig = plt.figure(figsize=(20,6))
plt.title("Feature importances by RandomTreeClassifier")
plt.bar(range(len(indices)), importances[indices], color='lightblue', align="center")
plt.step(range(len(indices)), np.cumsum(importances[indices]), where='mid', label='Cumulative')
plt.xticks(range(len(indices)), feat_names[indices], rotation='vertical',fontsize=9)
plt.xlim([-1, len(indices)])
plt.show()data_ls = data_ls.drop(['LOCAL_CALLING_RATE_TREND',……,'SUB_TYPE'], axis=1)第三步、LR模型训练
# 构建X变量和Y变量。
x_feature = list(data_ls.columns)
x_feature.remove('IS_LIUSHI')
x_val = data_ls[x_feature]
y_val = data_ls['IS_LIUSHI']
## 训练与预测数据处理
def data_spilt(raw_data):
x_data = raw_data[x_feature]
y_data = raw_data['IS_LIUSHI']
x_train,x_test, y_train, y_test = train_test_split(x_data, y_data,test_size=0.3,random_state = 0)
return x_train,x_test, y_train, y_test
x_train,x_test, y_train, y_test = data_spilt(data_ls)
############## 模型训练及输出 #################
def model_train(x_train, y_train, model='LR'):
if model == 'LR':
res_model = LogisticRegression()
res_model = res_model.fit(x_train, y_train)
list_feature_importances = [x for x in res_model.coef_[0]]
list_index = list(x_train.columns)
feature_importances = pd.DataFrame(list_feature_importances, list_index)
else:
pass
return res_model, feature_importances;
res_model, feature_importances = model_train(x_train, y_train, model='LR')
print (u"指标系数为:\n", feature_importances[0].order(ascending=False), u"\n常数项为:", res_model.intercept_)
print (u"重要变量贡献度为:\n", abs(feature_importances[0]).order(ascending=False))第四步、模型预测及评估
def model_predict(res_model, input_data, alpha=0.5):
data_proba = pd.DataFrame(res_model.predict_proba(input_data))
data_proba.columns = ['neg', 'pos']
data_proba['res'] = data_proba['pos'].apply(lambda x: np.where(x >= alpha, 1, 0))
return data_proba
def model_evaluate(y_true, y_pred):
y_true = np.array(y_true)
y_true.shape = (len(y_true),)
y_pred = np.array(y_pred)
y_pred.shape = (len(y_pred),)
print(metrics.classification_report(y_true, y_pred))
y_pred = model_predict(res_model, x_test)
y_pred = y_pred['res']
model_evaluate(y_test, y_pred)
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, y_pred)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
def plot_confusion_matrix(cm, classes,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=0)
plt.yticks(tick_marks, classes)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix , classes=class_names , title='Confusion matrix')
plt.show()
## 绘制 ROC曲线 ##################
fpr, tpr, thresholds = roc_curve(y_test, y_pred)
roc_auc = auc(fpr,tpr)
plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, 'b',label='AUC = %0.5f'% roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([-0.1,1.0])
plt.ylim([-0.1,1.01])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()结果显示为准确率0.28,召回率0.45,F值0.345,相比原始数据的自然流失率0.043,模型准确率有显著提高。
第五步、模型优化
上一个步骤中,我们的模型训练和测试都在同一个数据集上进行,这样导致模型产生过拟合的问题,下边进行优化模型训练 ,结合cross-validation(交叉验证法)和grid search(模型调优算法:网格搜索调优参数)重新训练模型。
# 构建参数组合
param_grid = {'C': [0.01,0.1, 1, 10, 100, 1000,],
'penalty': [ 'l1', 'l2']}
grid_search = GridSearchCV(LogisticRegression(), param_grid, cv=10)
grid_search.fit(x_train, y_train) 模型再次评估:
results = pd.DataFrame(grid_search.cv_results_)
best = np.argmax(results.mean_test_score.values)
print("Best parameters: {}".format(grid_search.best_params_))
print("Best cross-validation score: {:.5f}".format(grid_search.best_score_))
y_pred = grid_search.predict(x_test)
print("Test set accuracy score: {:.5f}".format(accuracy_score(y_test, y_pred,)))
print(classification_report(y_test, y_pred))
print("Best parameters: {}".format(grid_search.best_params_))
print("Best cross-validation score: {:.5f}".format(grid_search.best_score_))
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, y_pred)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix , classes=class_names , title='Confusion matrix')
plt.show()解决不同的问题,通常需要不同的指标来度量模型的性能。例如我们希望用算法来预测癌症是否是恶性的,假设100个病人中有5个病人的癌症是恶性,对于医生来说,尽可能提高模型的查全率(recall)比提高查准率(precision)更为重要,因为站在病人的角度,发生漏发现癌症为恶性比发生误判为癌症是恶性更为严重。
y_pred_proba = grid_search.predict_proba(x_test)
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9] # 设定不同阈值
plt.figure(figsize=(15,10))
j = 1
for i in thresholds:
y_test_predictions_high_recall = y_pred_proba[:,1] > i
plt.subplot(3,3,j)
j += 1
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, y_test_predictions_high_recall)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
class_names = [0,1]
plot_confusion_matrix(cnf_matrix , classes=class_names , title='Thresholds >= ' + str(i))
plt.show()
# 不同阈值下ROC曲线
from itertools import cycle
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
colors = cycle(['navy', 'turquoise', 'darkorange', 'cornflowerblue', 'teal', 'red', 'yellow', 'green', 'blue','black'])
plt.figure(figsize=(12,5))
j = 1
for i,color in zip(thresholds,colors):
y_test_predictions_prob = y_pred_proba[:,1] > i
precision, recall, thresholds = precision_recall_curve(y_test, y_test_predictions_prob)
area = auc(recall, precision)
# Plot Precision-Recall curve
plt.plot(recall, precision, color=color,
label='Threshold: %s, AUC=%0.5f' %(i , area))
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title('Precision-Recall Curve')
plt.legend(loc="lower left")
plt.show()令alpha = 0.5,结果显示为准确率0.307,召回率0.47,F值0.371。可以看出,结合cross-validation和grid search技术训练模型对模型效果有显著地提升。
precision和recall是一组矛盾的变量。从上面混淆矩阵和PRC曲线可以看到,阈值越小,recall值越大,模型能找出流失用户的数量也就更多,但换来的代价是误判的数量也较大。随着阈值的提高,recall值逐渐降低,precision值也逐渐提高,误判的数量也随之减少。通过调整模型阈值,控制模型流失发生的力度,若想找出更多的用户流失就设置较小的阈值,反之,则设置较大的阈值。
实际业务中,阈值的选择取决于公司业务边际利润和边际成本的比较;当模型阈值设置较小的值,确实能找出更多的即将流失用户,但随着误判数量增加,不仅加大了市场部营销人员的工作量,也会降低误判为流失用户的消费体验,从而导致客户满意度下降,如果某个模型阈值能让业务的边际利润和边际成本达到平衡时,则该模型的阈值为最优值。
后边按照月份往后平滑数据进行模型平滑检验以及模型的持续优化,这里不再展示。