目标检测回归损失函数小结IOU、GIOU、DIOU、CIOU

L1 loss

本方法由微软rgb大神提出，Fast RCNN论文提出该方法。假设x为预测框和真实框之间的数值差异，常用的L1 Loss定义为： $L_1=|x|$
导数：

L2 Loss

定义为：$L_2=x^2$
导数：

smoothL1 Loss

定义为：

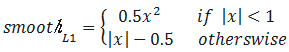
导数：

从损失函数对x的导数可知： L1损失函数对x的导数为常数，在训练后期，x很小时，如果learning rate 不变，损失函数会在稳定值附近波动，很难收敛到更高的精度。 L2 损失函数对x的导数在x值很大时，其导数也非常大，在训练初期不稳定。 smoothL1 完美的避开了L1 和L2 损失的缺点.

实际目标检测框回归任务中的损失loss为:

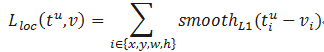
其中$v=(v_x,v_y,v_w,v_h)$表示GT的框坐标，$t^u=(t_x^u,t_y^u,t_w^u,t_h^u)$表示预测的框坐标，即分别求4个点的loss，然后相加作为Bounding Box Regression Loss。

缺点：
上面的三种Loss用于计算目标检测的Bounding Box Loss时，独立的求出4个点的Loss，然后进行相加得到最终的Bounding Box Loss，这种做法的假设是4个点是相互独立的，实际是有一定相关性的

实际评价框检测的指标是使用IOU，这两者是不等价的，多个检测框可能有相同大小的smoothL1 Loss，但IOU可能差异很大，为了解决这个问题就引入了IOU LOSS

IOU(Intersection over Union)

IoU就是我们所说的交并比，是目标检测中最常用的指标，在anchor-based的方法中，他的作用不仅用来确定正样本和负样本，还可以用来评价输出框（predict box）和ground-truth的距离。

$IOU=(A\bigcap B)/(A\bigcup B)$

可以说它可以反映预测检测框与真实检测框的检测效果。

还有一个很好的特性就是尺度不变性，也就是对尺度不敏感（scale invariant）， 在regression任务中，判断predict box和gt的距离最直接的指标就是IoU。(满足非负性；同一性；对称性；三角不等性)

检测评价的方式是使用IoU,而实际回归坐标框的时候是使用4个坐标点，如下图所示，是不等价的；L1或者L2 Loss相同的框，其IoU 不是唯一的。通过4个点回归坐标框的方式是假设4个坐标点是相互独立的，没有考虑其相关性，实际4个坐标点具有一定的相关性。基于L1和L2的距离的loss对于尺度不具有不变性

图(a)中的三组框具有相同的L2 Loss，但其IoU差异很大；图（b）中的三组框具有相同的L1 Loss,但IoU 同样差异很大，说明L1,L2这些Loss用于回归任务时，不能等价于最后用于评测检测的IoU.

上图中的红色点表示目标检测网络结构中Head部分上的点（i,j），绿色的框表示Ground truth框, 蓝色的框表示Prediction的框，IoU loss的定义如上，先求出2个框的IoU，然后再求个-ln(IoU)，实际很多是直接定义为IoU Loss = 1-IoU

论文链接：https://arxiv.org/pdf/1608.01471.pdf
Python代码：

import numpy as np
def Iou(box1, box2, wh=False):
    if wh == False:
	    xmin1, ymin1, xmax1, ymax1 = box1
	    xmin2, ymin2, xmax2, ymax2 = box2
    else:
	    xmin1, ymin1 = int(box1[0]-box1[2]/2.0),int(box1[1]-box1[3]/2.0)
	    xmax1, ymax1 = int(box1[0]+box1[2]/2.0),int(box1[1]+box1[3]/2.0)
	    xmin2, ymin2 = int(box2[0]-box2[2]/2.0),int(box2[1]-box2[3]/2.0)
	    xmax2, ymax2 = int(box2[0]+box2[2]/2.0),int(box2[1]+box2[3]/2.0)
    # 获取矩形框交集对应的左上角和右下角的坐标（intersection）
    xx1 = np.max([xmin1, xmin2])
    yy1 = np.max([ymin1, ymin2])
    xx2 = np.min([xmax1, xmax2])
    yy2 = np.min([ymax1, ymax2])	
    # 计算两个矩形框面积
    area1 = (xmax1-xmin1) * (ymax1-ymin1) 
    area2 = (xmax2-xmin2) * (ymax2-ymin2)
    inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))　#计算交集面积
    iou = inter_area / (area1+area2-inter_area+1e-6) 　#计算交并比

    return iou

作为损失函数会出现的问题(缺点)

如果两个框没有相交，根据定义，IoU=0，不能反映两者的距离大小（重合度）。同时因为loss=0，没有梯度回传，无法进行学习训练。

IoU无法精确的反映两者的重合度大小。如下图所示，三种情况IoU都相等，但看得出来他们的重合度是不一样的，IoU值不能反映两个框是如何相交的，左边的图回归的效果最好，右边的最差。

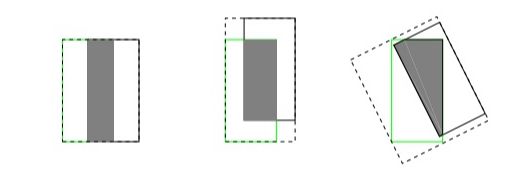
如上图所示，三种不同相对位置的框拥有相同的IoU=0.33值，但是拥有不同的GIoU=0.33，0.24，-0.1。当框的对齐方向更好一些时GIoU的值会更高一些

GIOU(Generalized Intersection over Union)

GIoU的性质：
GIoU和IoU一样，可以作为一种距离的衡量方式，$L_{GIOU}=1-GIOU$
GIOU具有尺度不变性
对于$\forall A,B$有$GIOU（A,B）\le IOU（A,B）$且$0\le IOU（A,B）\le 1$，因此$-1\le GIOU（A,B）\le 1$当$A\to B$时，两者相同都等于1，此时GIOU等于1

当A和B相交时，$GIOU（A,B）=-1$


论文链接：https://arxiv.org/abs/1902.09630
github链接：https://github.com/generalized-iou/g-darknet
参考链接：目标检测算法之CVPR2019 GIoU Loss
python代码：

def Giou(rec1,rec2):
    #分别是第一个矩形左右上下的坐标
    x1,x2,y1,y2 = rec1 
    x3,x4,y3,y4 = rec2
    iou = Iou(rec1,rec2)
    area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
    area_1 = (x2-x1)*(y1-y2)
    area_2 = (x4-x3)*(y3-y4)
    sum_area = area_1 + area_2

    w1 = x2 - x1   #第一个矩形的宽
    w2 = x4 - x3   #第二个矩形的宽
    h1 = y1 - y2
    h2 = y3 - y4
    W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)    #交叉部分的宽
    H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)    #交叉部分的高
    Area = W*H    #交叉的面积
    add_area = sum_area - Area    #两矩形并集的面积

    end_area = (area_C - add_area)/area_C    #闭包区域中不属于两个框的区域占闭包区域的比重
    giou = iou - end_area
return giou

DIoU Loss

GIoU Loss不足：

基于IoU和GIoU存在的问题，作者提出了两个问题：
第一：直接最小化预测框与目标框之间的归一化距离是否可行，以达到更快的收敛速度。

第二：如何使回归在与目标框有重叠甚至包含时更准确、更快。

好的目标框回归损失应该考虑三个重要的几何因素：重叠面积，中心点距离，长宽比。基于问题一，作者提出了DIoU Loss,相对于GIoU Loss收敛速度更快，该Loss考虑了重叠面积和中心点距离，但没有考虑到长宽比；针对问题二，作者提出了CIoU Loss，其收敛的精度更高，以上三个因素都考虑到了。

Distance-IoU Loss：

通常基于IoU-based的loss可以定义为$L=1-IOU+R(B,B^{gt})$其中$R(B,B^{gt})$定义为预测框$B$和目标框$B^{gt}$的惩罚项。

DIOU的惩罚项表示为$R_{DIOU}={\rho }^2(b,b^{gt})/c^2$,其中b和$b^{gt}$分别表示$B$和$B^{gt}$的中心点，ρ（∙）表示欧式距离，$c$表示$B$和$B^{gt}$的最小外界矩形的对角线距离，如下图所示。可以将DIoU替换IoU用于NMS算法当中，也即论文提出的DIoU-NMS,实验结果表明有一定的提升。

DIoU Loss function定义为：
$L_{DIOU}=1-IOU+{\rho }^2(b,b^{gt})/c^2$

论文地址: https://arxiv.org/pdf/1911.08287.pdf
GitHub连接：https://github.com/Zzh-tju/DIoU-darknet

优点：
尺度不变性
当两个框完全重合时，$L_{IOU}=L_{GIOU}=L_{DIOU}=0$当2个框不相交时,$L_{GIOU}=L_{DIOU}\to 2$

与GIoU loss类似，DIoU loss（$L_{DIOU}=1-DIOU$）在与目标框不重叠时，仍然可以为边界框提供移动方向。
DIoU loss可以直接最小化两个目标框的距离，因此比GIoU loss收敛快得多。

对于包含两个框在水平方向和垂直方向上这种情况，DIoU损失可以使回归非常快，而GIoU损失几乎退化为IoU损失，收敛速度较慢。

DIoU还可以替换普通的IoU评价策略，应用于NMS中，使得NMS得到的结果更加合理和有效.

Python代码：

def Diou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    dious = torch.zeros((rows, cols))
    if rows * cols == 0:#
        return dious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        dious = torch.zeros((cols, rows))
        exchange = True
    # #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1] 
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]
    
    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2 
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2 
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:]) 
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2]) 
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:]) 
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    dious = inter_area / union - (inter_diag) / outer_diag
    dious = torch.clamp(dious,min=-1.0,max = 1.0)
    if exchange:
        dious = dious.T
    return dious

CIoU Loss

论文考虑到bbox回归三要素中的长宽比还没被考虑到计算中，因此，进一步在DIoU的基础上提出了CIoU。其惩罚项如下面公式：

$R_{CIOU}={\rho }^2(b,b^{gt})/c^2+\alpha v$, 其中$\alpha$是用于做trade-off的参数，是权重函数。是权重函数$\alpha v$,$\alpha =v/((1-IOU)+v)$，$v$是用来衡量长宽比一致性的参数，定义为$v=4/{\pi }^2(arctan(w^{gt}/h^{gt})-arctan(w/h){)}^2$

CIoU Loss function的定义为$L_{CIOU}=1-IOU+{\rho }^2(b,b^{gt})/c^2+\alpha v$

最后， CIoU loss的梯度类似于DIoU loss，但还要考虑$ v$ 的梯度。在长宽在[0,1] 的情况下, $w^2+h^2$的值通常很小，会导致梯度爆炸，因此在$1/(w^2+h^2)$ 实现时将替换成1

论文地址：https://arxiv.org/pdf/1911.08287.pdf
github地址： https://github.com/Zzh-tju/DIoU-darknet
python代码：

def bbox_overlaps_ciou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    cious = torch.zeros((rows, cols))
    if rows * cols == 0:
        return cious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        cious = torch.zeros((cols, rows))
        exchange = True

    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1]
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]

    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    u = (inter_diag) / outer_diag
    iou = inter_area / union
    with torch.no_grad():
        arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)
        v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
        S = 1 - iou
        alpha = v / (S + v)
        w_temp = 2 * w1
    ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)
    cious = iou - (u + alpha * ar)
    cious = torch.clamp(cious,min=-1.0,max = 1.0)
    if exchange:
        cious = cious.T
    return cious

参考博客：
https://zhuanlan.zhihu.com/p/104236411
https://zhuanlan.zhihu.com/p/94799295
https://blog.csdn.net/TJMtaotao/article/details/103317267