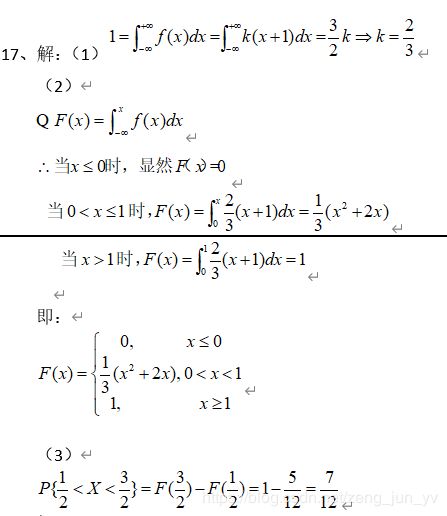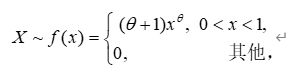概率论+往期考试卷
工程数学2018――2019学年
一、单项选择题
1.对掷一颗骰子的试验,将“出现偶数点”称为 ( D )
A、样本空间 B、必然事件
C、不可能事件 D、随机事件
2.若事件A、B 互不相容,则下列等式中未必成立的是 (C )
A、AB= ∅ \varnothing ∅ B、P(AB)=0
C、P(A)+P(B)=1 D、 P(A ∪ \cup ∪B)=P(A)+P(B)
分析:C项:P(A)+P(B)=1,当A与B对立时成立
3.设随机变量X的分布函数为F(x) ,下列说法中正确的是 ( D )
A、 F(x)是增函数 B、 F(x)必为(-∞,+∞) 上的连续函数
C、F( -∞)=1 D、 F(x) ≤ \leq ≤ 1
分析:D项正确:由于0≤F(x)≤1,F(x)的值域为[0,1];
A项:F(x)是不减函数,故错误;
B项:由于F(x)仅右连续,从而(B)不对;
C项:由于
![]()
,从而(C)不对。
4. 设总体 X服从正态分布N( μ \mu μ, σ 2 \sigma ^{2} σ2) ,其中 μ \mu μ已知, σ 2 \sigma ^{2} σ2未知, X 1 、 X 2 、 X 3 X_{1}、X_{2}、X_{3} X1、X2、X3是总体 X的一个简单随机样本,则下列表达式中不是统计量的是 ( C )
A、 X 1 + X 2 + X 3 X_{1}+X_{2}+X_{3} X1+X2+X3 B、min( X 1 , X 2 , X 3 X_{1},X_{2},X_{3} X1,X2,X3) C、 ∑ i = 1 3 X i 2 σ 2 \sum_{i=1}^{3}\frac{X_{i}^{2}}{\sigma ^{2}} ∑i=13σ2Xi2 D、 X ‾ \overline{X} X+2 μ \mu μ
分析:由于X服从正态分布N(μ,σ2),其中μ已知,σ2未知,因此未知参数只有 σ \sigma σ。
选项A、B都是关于样本的函数,它们是统计量;
选项D虽然含有参数μ,但μ是已知的,因此也是统计量;
选项C由于含有未知参数σ,它不是统计量.
故选:C
5.设 X 1 、 X 2 、 X 3 、 X 4 X_{1}、X_{2}、X_{3}、X_{4} X1、X2、X3、X4是来自均值为 θ \theta θ的指数分布的样本,其中 θ \theta θ 未知,以下估计量中哪个是 θ \theta θ 的无偏估计量? ( A )
A、 X 1 + X 2 + 2 X 3 + X 4 5 \frac{X_{1}+X_{2}+2X_{3}+X_{4}}{5} 5X1+X2+2X3+X4
B、 3 X 1 + X 2 + X 3 + X 4 7 \frac{3X_{1}+X_{2}+X_{3}+X_{4}}{7} 73X1+X2+X3+X4
C、 X 1 + X 2 4 \frac{X_{1}+X_{2}}{4} 4X1+X2 + X 3 + X 4 3 \frac{X_{3}+X_{4}}{3} 3X3+X4
D、 X 1 + X 2 + X 3 + X 4 3 \frac{X_{1}+X_{2}+X_{3}+X_{4}}{3} 3X1+X2+X3+X4
分析:如果指数分布 θ \theta θ ~e(λ),那么E( θ \theta θ )== 1 λ \frac{1}{ λ} λ1 D( θ \theta θ )= 1 λ 2 \frac{1}{ λ^{2}} λ21
无偏估计量的定义是:设( θ ^ \widehat{\theta} θ )是 θ \theta θ的一个估计量,若E( θ ^ \widehat{\theta} θ )= θ \theta θ ,则称 θ ^ \widehat{\theta} θ 是 θ \theta θ的无偏估计量
A项:E( X 1 + X 2 + 2 X 3 + X 4 5 \frac{X_{1}+X_{2}+2X_{3}+X_{4}}{5} 5X1+X2+2X3+X4 )=E( 1 λ + 1 λ + 2 1 λ + 1 λ 5 \frac{\frac{1}{ λ}+\frac{1}{ λ}+2\frac{1}{ λ}+\frac{1}{ λ}}{5} 5λ1+λ1+2λ1+λ1 )= 1 λ \frac{1}{ λ} λ1,故A项正确。
6.若随机变量X,Y 独立,下列等式中错误的是 ( D)
A、对任何实数a,b ,事件{X ≤ \leq ≤a} 和事件 {Y ≤ \leq ≤b}独立
B、 P(X ≤ \leq ≤x,Y ≤ \leq ≤y)=P(X ≤ \leq ≤x)P(Y ≤ \leq ≤y)
C、 F(x,y)= F X ( x ) F Y ( y ) F_{X}(x)F_{Y}(y) FX(x)FY(y)
D、 ρ X Y \rho_{XY} ρXY=1
分析:相互独立是设A,B是两事件,如果满足等式P(AB)=P(A)P(B),则称事件A,B相互独立,简称A,B独立.A、B、C正确·
D(X)= E ( X 2 ) + E ( X ) 2 E(X^{2})+E(X)^{2} E(X2)+E(X)2
ρ X Y \rho_{XY} ρXY= C o v ( X , Y ) D ( X ) D ( Y ) \frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}} D(X)D(Y)Cov(X,Y)
若随机变量X,Y 独立,Cov(X,Y)=0;
故 ρ X Y \rho_{XY} ρXY=0;因此(D)错
7.对于一个原假设为 的假设检验问题,有可能犯的第一类错误是指( B )
A、 H 0 H_{0} H0为真时,接受 H 0 H_{0} H0
B、 H 0 H_{0} H0为真时,拒绝 H 0 H_{0} H0
C、 H 0 H_{0} H0不真时,接受 H 0 H_{0} H0
D、 H 0 H_{0} H0不真时,拒绝 H 0 H_{0} H0
二、填空题(每小题3分,共24分)
8.设A,B 为随机事件,P(A)=0.5 ,P(B)=0.6 ,P(B|A)=0.8,则P(B ∪ \cup ∪A)= 0.7_ .
分析:P(BUA)为0.7。计算过程如下:
P(A)=0.5。
P(B)=0.6。
P(B|A)=P(AB)/P(A)=0.8。
所以P(AB)=0.4。
P(A+B)=P(A)+P(B)-P(AB)=0.5+0.6-0.4=0.7。
所以P(BUA)=P(A+B)=0.7。
扩展资料:
常用概率公式
1、设A、B是互不相容事件(AB=φ),则:P(A∪B)=P(A)+P(B)
推论1:设A1、A2、…、An互不相容,则:P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An)
推论2:设A1、A2、…、An构成完备事件组,则:P(A1+A2+…+An)=1
推论3:为事件A的对立事件。
推论4:若B包含A,则P(B-A)=P(B)-P(A)
推论5(广义加法公式):对任意两个事件A与B,有P(A∪B)=P(A)+P(B)-P(AB)
2、条件概率:已知事件B出现的条件下A出现的概率,称为条件概率,记作:P(A|B)条件概率计算公式:
当P(A)>0,P(B|A)=P(AB)/P(A)
当P(B)>0,P(A|B)=P(AB)/P(B)
3、乘法公式
P(AB)=P(A)×P(B|A)=P(B)×P(A|B)
推广:P(ABC)=P(A)P(B|A)P(C|AB)
9. 一大楼装有5个同类型的供水设备,调查表明在任一时刻t每个设备使用的概率为 0.3,则在同一时刻恰有2个设备被使用的概率是______0.3087________.
n重复相同实验,为二项分布
故P(2)= C 5 2 ∗ 0. 3 2 ∗ ( 1 − 0.3 ) ( 5 − 2 ) C_{5}^{2}* 0.3^{2} *(1-0.3)^{(5-2)} C52∗0.32∗(1−0.3)(5−2)=0.3087
10. 设随机变量X ,Y 相互独立,且X:B(100,0.6) ,Y:P(2) ,则 D(2X-Y)= _98 .
分析:因为1、D(C)=0;
2、D(aX+b)= a 2 a^{2} a2D(X);
3、D(X ± \pm ±Y)=D(X)+D(Y) ± \pm ±DOV(X,Y)
又设随机变量X ,Y 相互独立DOV(X,Y)=0;
X:B(100,0.6),可知为二项分布,D(X)=100* 0.6* (1-0.6)=24;
Y:P(2) ,可知为泊松分布,则D(Y)=λ=2;
则D(2X - Y )
=4D(X)+D(Y)=24*4+2=98
11.三人独立地去破译一份密码,各人能译出的概率分别为 1 6 \frac{1}{6} 61 , 1 5 \frac{1}{5} 51 , 1 4 \frac{1}{4} 41此密码被译出的概率为 0.5___ .
分析:密码被译出的概率即为至少一人破译:1-(1- 1 6 \frac{1}{6} 61)(1- 1 5 \frac{1}{5} 51)(1- 1 4 \frac{1}{4} 41)=0.5
12. 若X与Y相互独立,则Cov(X,Y)= _0__ .
13.随机变量 ξ \xi ξ~ χ 2 ( n ) \chi^{2}(n) χ2(n) , η \eta η~ χ 2 ( m ) \chi^{2}(m) χ2(m) , ξ \xi ξ, η \eta η 独立,则 ξ \xi ξ+ η \eta η~ χ 2 ( n + m ) \chi^{2}(n+m) χ2(n+m)_ .
14. 设 X 1 、 X 2 、 L 、 X 5 X_{1}、X_{2}、L、X_{5} X1、X2、L、X5 是总体 X~N(0,1)的简单随机样本,则当K= 6 2 \frac{\sqrt{6}}{2} 26_ 时,Y= k ( X 1 + X 2 ) X 3 2 + X 4 2 + X 5 2 \frac{k(X_{1}+X_{2})}{\sqrt{X_{3}^{2}+X_{4}^{2}+X_{5}^{2}}} X32+X42+X52k(X1+X2)~t(3) ;
分析:因为 X 1 、 X 2 、 L 、 X 5 X_{1}、X_{2}、L、X_{5} X1、X2、L、X5 是总体 X~N(0,1)的简单随机样本
且 k ( X 1 + X 2 ) X 3 2 + X 4 2 + X 5 2 \frac{k(X_{1}+X_{2})}{\sqrt{X_{3}^{2}+X_{4}^{2}+X_{5}^{2}}} X32+X42+X52k(X1+X2)= 2 k 3 \frac{\sqrt{2}k}{\sqrt{3}} 32k,
为使 k ( X 1 + X 2 ) X 3 2 + X 4 2 + X 5 2 \frac{k(X_{1}+X_{2})}{\sqrt{X_{3}^{2}+X_{4}^{2}+X_{5}^{2}}} X32+X42+X52k(X1+X2)~t(3),
只需 2 k 3 \frac{\sqrt{2}k}{\sqrt{3}} 32k=1即可,
得 a = 6 2 \frac{\sqrt{6}}{2} 26
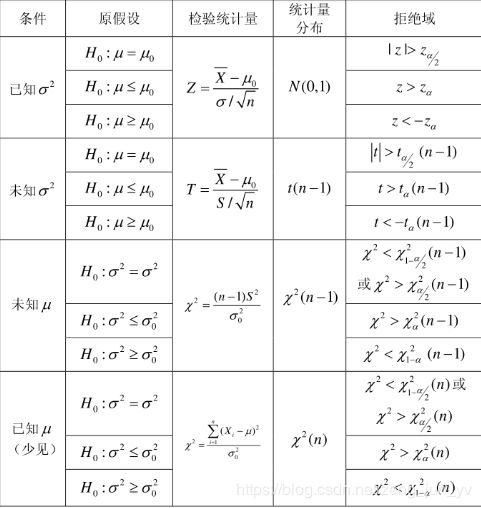
15.在对单个正态总体均值的假设检验中,当总体方差已知时,选用 Z或U_ 检验法
三、解答题(每题11分,共55分)
16. 已知男子有5%是色盲患者,女子有0.25%是色盲患者.今从男女人数相等的人群中随机抽选一人.
(1)求此人是色盲患者的概率;
(2)若此人恰好是色盲,则此人是女性的概率是多少?
分析:全概率公式:P(发生某事)=P(A出现)P(A发生某事)+P(B出现)P(B发生某事)…
贝叶斯公式:P(已知有个体发生某事是A发出的)= P ( A 出 现 ) P ( A 发 生 某 事 ) P ( 发 生 某 事 ) − − − − − − 》 ( 全 概 率 公 式 ) \frac{P(A出现)P(A发生某事)}{P(发生某事)------》(全概率公式)} P(发生某事)−−−−−−》(全概率公式)P(A出现)P(A发生某事)

17.设随机变量 的密度函数为:
f ( x ) f(x) f(x)= { k ( x + 1 ) , 0 < x < 1 0 , 其 他 \begin{cases}k(x+1)& \text{ , } 0{k(x+1)0,其他 , 0<x<1
求(1)常数k ;
(2) X的分布函数F(x) ;
(3)P{ 1 2 \frac{1}{2} 21 ≤ \leq ≤ 3 2 \frac{3}{2} 23} .
分析·:
一、已知 F X ( x ) F_{X}(x) FX(x)或 f X ( x ) f_{X}(x) fX(x)含未知数,求未知数:
- F X F_{X} FX(-∞)=0;
- F X F_{X} FX(+∞)=0;
- F 上 F_{上} F上(分段点)= F 下 F_{下} F下(分段点)(断点值相同)
- ∫ − ∞ + ∞ \int_{-∞}^{+∞} ∫−∞+∞ f X ( x ) d x f_{X}(x)d_{x} fX(x)dx=1;
二、 F X ( x ) F_{X}(x) FX(x)= ∫ − ∞ + ∞ \int_{-∞}^{+∞} ∫−∞+∞ f X ( x ) d x f_{X}(x)d_{x} fX(x)dx
三、已知 F X ( x ) F_{X}(x) FX(x)或 f X ( x ) f_{X}(x) fX(x)中一种,求P,
P(a
18.一工厂生产的某种设备的寿命 (以年计)服从指数分布,概率密度为
工厂规定,出售的设备在售出一年之内损坏可予以调换.若不需调换,每台设备工厂可以赢利1000元;若需要调换,每台设备工厂会亏损500元,试求厂方出售一台设备净赢利的数学期望.
19.设总体
其中, X 1 、 X 2 、 L 、 X n X_{1}、X_{2}、L、X_{n} X1、X2、L、Xn 是X的一个样本,求:
(1) θ \theta θ的矩估计量;
(2) θ \theta θ最大似然估计量.
20.某种矿砂的5个样品中的含镍量(%)经测定为:
3.24 3.26 3.24 3.27 3.25
设含镍量服从正态分布,问在 α \alpha α =0.01下能否接收假设:这批矿砂的含镍量为3.25?
( t 0.005 ( 4 ) t_{0.005}(4) t0.005(4)= 4.6041 , 5 \sqrt{5} 5=2.236 )
分析:![]()
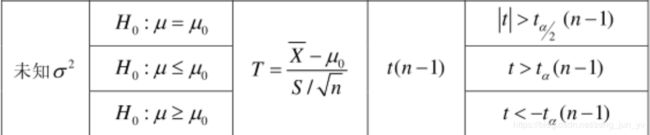
S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 S^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2} S2=n−11∑i=1n(Xi−X)2