哈密顿图 哈密顿回路 哈密顿通路(Hamilton)
概念:
哈密顿图:图G的一个回路,若它通过图的每一个节点一次,且仅一次,就是哈密顿回路.存在哈密顿回路的图就是哈密顿图.哈密顿图就是从一点出发,经过所有的必须且只能一次,最终回到起点的路径.图中有的边可以不经过,但是不会有边被经过两次.
与欧拉图的区别:欧拉图讨论的实际上是图上关于边的可行便利问题,而哈密顿图的要求与点有关.
判定:
一:Dirac定理(充分条件)
设一个无向图中有N个顶点,若所有顶点的度数大于等于N/2,则哈密顿回路一定存在.(N/2指的是⌈N/2⌉,向上取整)
二:基本的必要条件
设图G=
三:竞赛图(哈密顿通路)
N(N>=2)阶竞赛图一点存在哈密顿通路.
算法:
一:在Dirac定理的前提下构造哈密顿回路
过程:
1:任意找两个相邻的节点S和T,在其基础上扩展出一条尽量长的没有重复结点的路径.即如果S与结点v相邻,而且v不在路径S -> T上,则可以把该路径变成v -> S -> T,然后v成为新的S.从S和T分别向两头扩展,直到无法继续扩展为止,即所有与S或T相邻的节点都在路径S -> T上.
2:若S与T相邻,则路径S -> T形成了一个回路.
3:若S与T不相邻,可以构造出来一个回路.设路径S -> T上有k+2个节点,依次为S, v1, v2, ..., vk, T.可以证明存在节点vi(i属于[1, k]),满足vi与T相邻,且vi+1与S相邻.找到这个节点vi,把原路径变成S -> vi -> T -> vi+1 ,即形成了一个回路.
4:到此为止,已经构造出来了一个没有重复节点的的回路,如果其长度为N,则哈密顿回路就找到了.如果回路的长度小于N,由于整个图是连通的,所以在该回路上,一定存在一点与回路之外的点相邻.那么从该点处把回路断开,就变回了一条路径,同时还可以将与之相邻的点加入路径.再按照步骤1的方法尽量扩展路径,则一定有新的节点被加进来.接着回到路径2.
证明:
跟据鸽巢定理,既然与S和T相邻的点都在路径上,它们分布的范围只有v1,v2---,vk这k个点,k<=N-2,跟据哈密顿回路的第一个判断条件,d(S)+d(T)>=N,那么v1,v2,---vk这k个点中一定有至少2个点同时与S和T相连,根据鸽巢定理,肯定存在一个与S相邻的点vi和一个与T相邻的点vj,满足j=i+1
伪代码:
设s为哈密顿回路的起始点,t为哈密顿回路中终点s之前的点.ans[]为最终的哈密顿回路.倒置的意思指的是将数组对应的区间中数字的排列顺序反向.
1:初始化,令s = 1,t为s的任意一个邻接点.
2:如果ans[]中元素的个数小于n,则从t开始向外扩展,如果有可扩展点v,放入ans[]的尾部,并且t=v,并继续扩展,如无法扩展进入步骤3.
3:将当前得到的ans[]倒置,s和t互换,从t开始向外扩展,如果有可扩展点v,放入ans[]尾部,并且t=v,并继续扩展.如无法扩展进入步骤4.
4:如果当前s和t相邻,进入步骤5.否则,遍历ans[],寻找点ans[i],使得ans[i]与t相连并且ans[i +1]与s相连,将从ans[i + 1]到t部分的ans[]倒置,t=ans[i +1],进如步骤5.
5:如果当前ans[]中元素的个数等于n,算法结束,ans[]中保存了哈密顿回路(可看情况是否加入点s).否则,如果s与t连通,但是ans[]中的元素的个数小于n,则遍历ans[],寻找点ans[i],使得ans[i]与ans[]外的一点(j)相连,则令s=ans[i - 1],t = j,将ans[]中s到ans[i - 1]部分的ans[]倒置,将ans[]中的ans[i]到t的部分倒置,将点j加入到ans[]的尾部,转步骤2.
时间复杂度:
如果说每次到步骤5算一轮的话,那么由于每一轮当中至少有一个节点被加入到路径S -> T中,所以总的轮数肯定不超过n轮,所以时间复杂度为O(n^2).空间上由于边数非常多,所以采用邻接矩阵来存储比较适合.
附上模板:
const int maxN = 100;
inline void reverse(int arv[maxN + 7], int s, int t){//将数组anv从下标s到t的部分的顺序反向
int temp;
while(s < t){
temp = arv[s];
arv[s] = arv[t];
arv[t] = temp;
s++;
t--;
}
}
void Hamilton(int ans[maxN + 7], bool map[maxN + 7][maxN + 7], int n){
int s = 1, t;//初始化取s为1号点
int ansi = 2;
int i, j;
int w;
int temp;
bool visit[maxN + 7] = {false};
for(i = 1; i <= n; i++) if(map[s][i]) break;
t = i;//取任意邻接与s的点为t
visit[s] = visit[t] = true;
ans[0] = s;
ans[1] = t;
while(true){
while(true){//从t向外扩展
for(i = 1; i <= n; i++){
if(map[t][i] && !visit[i]){
ans[ansi++] = i;
visit[i] = true;
t = i;
break;
}
}
if(i > n) break;
}
w = ansi - 1;//将当前得到的序列倒置,s和t互换,从t继续扩展,相当于在原来的序列上从s向外扩展
i = 0;
reverse(ans, i, w);
temp = s;
s = t;
t = temp;
while(true){//从新的t继续向外扩展,相当于在原来的序列上从s向外扩展
for(i = 1; i <= n; i++){
if(map[t][i] && !visit[i]){
ans[ansi++] = i;
visit[i] = true;
t = i;
break;
}
}
if(i > n) break;
}
if(!map[s][t]){//如果s和t不相邻,进行调整
for(i = 1; i < ansi - 2; i++)//取序列中的一点i,使得ans[i]与t相连,并且ans[i+1]与s相连
if(map[ans[i]][t] && map[s][ans[i + 1]])break;
w = ansi - 1;
i++;
t = ans[i];
reverse(ans, i, w);//将从ans[i +1]到t部分的ans[]倒置
}//此时s和t相连
if(ansi == n) return;//如果当前序列包含n个元素,算法结束
for(j = 1; j <= n; j++){//当前序列中元素的个数小于n,寻找点ans[i],使得ans[i]与ans[]外的一个点相连
if(visit[j]) continue;
for(i = 1; i < ansi - 2; i++)if(map[ans[i]][j])break;
if(map[ans[i]][j]) break;
}
s = ans[i - 1];
t = j;//将新找到的点j赋给t
reverse(ans, 0, i - 1);//将ans[]中s到ans[i-1]的部分倒置
reverse(ans, i, ansi - 1);//将ans[]中ans[i]到t的部分倒置
ans[ansi++] = j;//将点j加入到ans[]尾部
visit[j] = true;
}
}在整个构造过程中,如果说每次到步骤5算做一轮的话,那么每一轮当中至少有一个节点被加入到路径S->T中,所以总的轮数肯定不超过n轮,实际上,不难看出该算法的复杂度是O(n^2),因此总共拓展了n轮路径,每步拓展最多枚举所有的节点。
二:N(N>=2)阶竞赛图构造哈密顿通路
N阶竞赛图:含有N个顶点的有向图,且每对顶点之间都有一条边.对于N阶竞赛图一定存在哈密顿通路.
数学归纳法证明竞赛图在n >= 2时必存在哈密顿路:
(1)n = 2时结论显然成立;
(2)假设n = k时,结论也成立,哈密顿路为V1, V2, V3, ..., Vk;
设当n = k+1时,第k + 1个节点为V(k+1),考虑到V(k+1)与Vi(1<=i<=k)的连通情况,可以分为以下两种情况.
1:Vk与V(k+1)两点之间的弧为
2:Vk与V(k+1)两点之间的弧为
证毕.
竞赛图构造哈密顿路时的算法同以上证明过程.
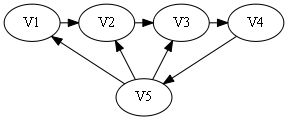
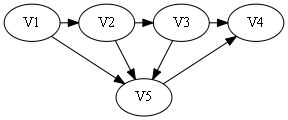
用图来说明:
假设此时已经存在路径V1 -> V2 -> V3 -> V4,这四个点与V5的连通情况有16种,给定由0/1组成的四个数,第i个数为0代表存在弧
sign[]={0, 0, 0, 0}.
很显然属于第二种情况,从后往前寻找不到1,即且不存在弧
则构造哈密顿路:V5 -> V1 -> V2 -> V3 -> V4.
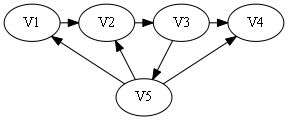
sign[]={0, 0, 0, 1}.
属于第一种情况,最后一个数字为1,即代表存在弧
则构造哈密顿路: V1 -> V2 -> V3 -> V4 -> V5.
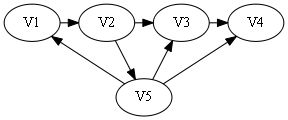
sign[]={0, 0, 1, 0}.
属于第二种情况,从后往前找到1出现的第一个位置为3.
构造哈密顿路: V1 -> V2 -> V3 -> V5 -> V4.
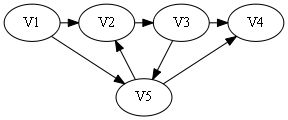
sign[]={0, 0, 1, 1}.
属于第一种情况,最后一个数字为1,即代表存在弧
则构造哈密顿路: V1 -> V2 -> V3 -> V4 -> V5.
sign[]={0, 1, 0, 0}.
属于第二种情况,从后往前找到1出现的第一个位置为2.
构造哈密顿路: V1 -> V2 -> V5 -> V3-> V4.
sign[]={0, 1, 0, 1}.
属于第一种情况,最后一个数字为1,即代表存在弧
则构造哈密顿路:V1 -> V2 -> V3 -> V4 -> V5.(就不举末尾为1的栗子了~~)
sign[]={1, 0, 1, 0}.
属于第二种情况,从后往前找到1出现的第一个位置为3.
构造哈密顿路: V1 -> V2 -> V3 -> V5-> V4.
sign[]={1, 1, 1, 0}.
属于第二种情况,从后往前找到1出现的第一个位置为3.
构造哈密顿路: V1 -> V2 -> V3 -> V5-> V4.
(还是举一个吧~~~)
sign[]={1, 1, 1, 1}.
同样最后一位为1,代表存在
则构造哈密顿路:V1 -> V2 -> V3 -> V4 -> V5.以上是当N=4时(N+1=5),用图来阐述算法的过程.
注意从后往前找不是找这个点编号之前的点,即不是按照编号来的,而是按照当前哈密顿序列从后往前找的.举个栗子:
4
2 1
1 3
3 2
4 1
4 2
4 3
第一步ans={1}
第二步ans={2,1}
第三步sign={0, 1}(map[3][2] = 0,map[3][1] = 1,当前序列为2,1) ,而不是{1, 0}(1,2),因为存在弧
代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int maxN = 200;
//The arv[] length is len, insert key befor arv[index]
inline void Insert(int arv[], int &len, int index, int key){
if(index > len) index = len;
len++;
for(int i = len - 1; i >= 0; --i){
if(i != index && i)arv[i] = arv[i - 1];
else{arv[i] = key; return;}
}
}
void Hamilton(int ans[maxN + 7], int map[maxN + 7][maxN + 7], int n){
int ansi = 1;
ans[ansi++] = 1;
for(int i = 2; i <= n; i++){//第一种情况,直接把当前点添加到序列末尾
if(map[i][ans[ansi - 1]] == 1)
ans[ansi++] = i;
else{
int flag = 0;
for(int j = ansi - 2; j > 0; --j){//在当前序列中,从后往前找到第一个满足条件的点j,使得存在且.
if(map[i][ans[j]] == 1){//找到后把该点插入到序列的第j + 1个点前.
flag = 1;
Insert(ans, ansi, j + 1, i);
break;
}
}
if(!flag)Insert(ans, ansi, 1, i);//否则说明所有点都邻接自点i,则把该点直接插入到序列首端.
}
}
}
int main()
{
//freopen("input.txt", "r", stdin);
int t;
scanf("%d", &t);
while(t--){
int N;
scanf("%d", &N);
int M = N * (N - 1) / 2;
int map[maxN + 7][maxN + 7] = {0};
for(int i = 0; i < M; i++){
int u, v;
scanf("%d%d", &u, &v);
//map[i][j]为1说明j < i,且存在弧,因为插入时只考虑该点之前的所有点的位置,与之后的点没有关系.所以只注重该点与其之前的点的连通情况.
if(u < v)map[v][u] = 1;
}
int ans[maxN + 7] = {0};
Hamilton(ans, map, N);
for(int i = 1; i <= N; i++)
printf(i == 1 ? "%d":" %d", ans[i]);
printf("\n");
}
return 0;
} void Hamilton(int ans[maxN + 7], int map[maxN + 7][maxN + 7], int n){
int nxt[maxN + 7];
memset(nxt, -1, sizeof(nxt));
int head = 1;
for(int i = 2; i <= n; i++){
if(map[i][head]){
nxt[i] = head;
head = i;
}else{
int pre = head, pos = nxt[head];
while(pos != -1 && !map[i][pos]){
pre = pos;
pos = nxt[pre];
}
nxt[pre] = i;
nxt[i] = pos;
}
}
int cnt = 0;
for(int i = head; i != -1; i = nxt[i])
ans[++cnt] = i;
}void Hamitton(bool reach[N + 7][N + 7], int n)
{
vector ans;
ans.push_back(1);
for(int i=2;i <= n;i++)
{
bool cont = false;
for(int j=0;j<(int)ans.size()-1;j++)
if(reach[ ans[j] ][i] && reach[i][ ans[j+1] ])
{
ans.insert(ans.begin()+j+1,i);
cont = true;
break;
}
if(cont)
continue;
if(reach[ ans.back() ][i])
ans.push_back(i);
else
ans.insert(ans.begin(),i);
}
for(int i=0;i