二维泊松方程数值解-五点差分法-共轭梯度法-python实现
松方程有很多现成的工具可以用,这里主要是为了加深对算法的理解。题目如下

题目的要点在于找到泊松方程的系数矩阵。在五点法里面,系数矩阵一共五条对角线,一条主对角线,四条副对角线。碰到边界的时候有的对角线上的值会变。
这里采用了五点差分法
具体算法见
https://wenku.baidu.com/view/bd04203a376baf1ffc4fadce.html?sxts=1548419750056
下面是n=4时系数矩阵的样子
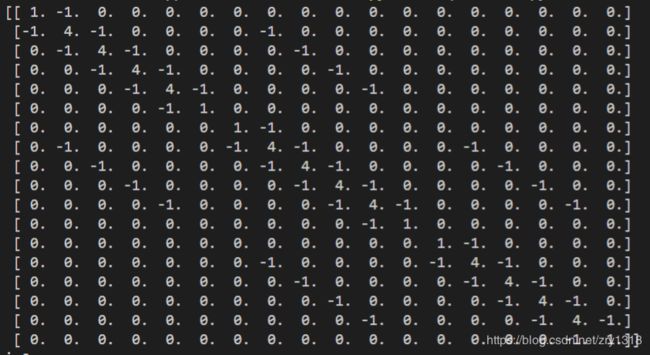
程序分以下几个子程序
coefficientmatrix(n):计算系数矩阵
网格向右平移半格以后,系数矩阵是一个[(n-1)(n+2)]^2的矩阵。由于泊松方程的系数矩阵比较确定,在内点对角线元素都是4,在边界上对角线元素是1,有四条斜对角线,值都是-1,根据这些规律直接设置好对角矩阵。
fij(): 计算f(x,y)
这个函数计算f(x,y),包括边界上的点
fxy(x,y)
方程的函数f
cg 共轭梯度法解方程
import numpy as np
import matplotlib.pyplot as plt
import math
from pylab import *
def coefficientmatrix(n):
n0 = (n-1)*(n+2)
A = np.zeros((n0, n0), dtype = float)
i = np.arange(0, n0) #设置中央对角线
A[i, i] = 4
j = np.arange(0, n0-1)#设置里面的两条斜对角线
A[j, j+1] = -1
A[j+1, j] = -1
k = np.arange(0, n0-n-2) #设置外面的两条斜对角线
A[k, k+n+2] = -1
A[k+n+2, k] = -1
for mm in range(0, n-1): #左边界
m = mm*(n+2) # n-1)*(n+2个元素
A[m, m] = 1.
A[m, m-1] = 0.
if m+n+2<n0:
A[m, m+n+2] = 0.
else:
A[m, m-n-2] = 0.
if mm>0:
A[m, m-n-2] = 0.
if mm>0: #右边界
A[m-1, m-1] = 1. #对角线
A[m-1, m-2] = -1. #对角线左边
A[m-1, m] = 0. #对角线右边
if m+n+1<n0:
A[m-1, m+n+1] = 0. #这一行右边次对角线元素为0
A[m-1, m-n-3] = 0.
else:
A[m-1, m-n-3] = 0. #这一行左边次对角线元素为0
A[n0-1, n0-1] = 1
A[n0-1, n0-2] = -1
A[n0-1, n0-n-3] = 0
return A
def fij(n, h, x, y, x_low, x_up, dy_left, dy_right) : #方程右端的值,包括两部分,一部分是边界上的,另一部分是函数本身的
n0 = (n-1)*(n+2)
f = np.zeros(n0, dtype = float)
f[-1] = dy_right #最后一个点 下面几行先设置边界上为0的点
m = np.arange(0, n0, n+2)
f[m] = dy_left #左边界
m2 = np.arange(n+1, n0, n+2) #右边界
f[m2] = dy_right
m3 = np.arange(1, n+1) #下边界
f[m3] = x_low
m4 = np.arange(n0-n-1, n0-1)
f[m4] = x_up
f2 = np.zeros((n-1, n+2), dtype = float) #计算每个网格上的方程右边函数值f(x, y)
for i in range(1, n): #沿着y方向,点数少
for j in range(0, n+2):
f2[i-1, j] = fxy(x[j], y[i])
f3 = f2.flatten() #变成一维数组
return f3*h*h+f #总的函数值 = f2*h^2+f
def fxy(x, y): #泊松方程右边的函数
pi = 3.141592653589793
f2 = 2.*pi*pi*math.cos(pi*x)*math.sin(pi*y)
return f2
def cg(A, b, x): #共轭斜量法
r = b-np.dot(A, x) #r=b-Ax r也是是梯度方向
p= np.copy(r)
i=0
while(max(abs(r))>1.e-10 and i < 100):
print('i', i)
print('r', r)
pap=np.inner(np.dot(A, p), p)
if pap==0: #分母太小时跳出循环
return x
print('pap=', pap)
alpha = np.inner(r, r)/pap #直接套用公式
x1 = x + alpha*p
r1 = r-alpha*np.dot(A, p)
beta = np.inner(r1, r1)/np.inner(r, r)
p1 = r1 +beta*p
r = r1
x = x1
p = p1
i=i+1
return x
n = 20 #网格数
A0 = coefficientmatrix(n) #计算系数矩阵
print(A0)
uij = np.zeros((n-1)*(n+2), dtype = float)#未知数,初始化
a_x = -1. #x方向边界
b_x = 1.
c_y = -1. #y方向边界
d_y = 1.
h = (b_x-a_x)/n
x_cood = np.arange(a_x-h/2., b_x+h, h) #n+2个网格,n+2个未知数
y_cood = np.arange(a_x, b_x+h, h) #y 有n+1个点,n-1个未知数
x_low = 0.
x_up = 0.
dy_left = 0.
dy_right = 0.
b_matrix = fij(n, h, x_cood, y_cood, x_low, x_up, dy_left, dy_right) #计算等式右端矩阵b
f_1d = cg(A0, b_matrix, uij) #调用共轭斜量法
result = f_1d.reshape(n-1, n+2) #转换成二维矩阵
plt.figure()
y_cood2 = np.arange(a_x+h, b_x, h) #y 有n+个点,n-1个未知数
print(y_cood2.shape)
contourf(x_cood, y_cood2, result, 80, cmap = 'seismic')
plt.colorbar()
plt.show()
plt.close()
