邻家割草问题JAVA实现
简化描述:
- 可以把草坪看成是一个N * M的矩阵,割草时需要 N台割草机水平方向穿过草地,M台 割草机垂直方向穿过草地。
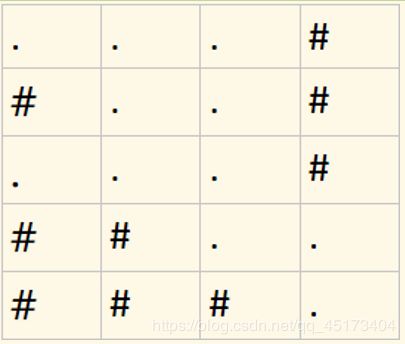
草地并不是完全平整的,有高有低;如图所示,高的地方用深色表示,矮的地方用浅色表示
2. 在走过不同高度的草地时,会消耗A元燃油燃油费;
(低--->高,高--->低,相同高度不花钱)
3. 为了节省燃油费,准备改造一些地形;可以给一些地块加高,或者把一些地块降低,对一个地块进行改造要花费B 元
4. 设计一个最小花费方案?
要求:
输入格式:
第一行:N M A B
| N |
矩阵有 N 行 |
| M |
矩阵有 M列 |
| A |
走过不同高度的地块的花费A |
| B |
调整地块的花费B |
接下来N行,M列,描述来草坪地形
| ‘#’ |
代表高的地块 |
| ‘.’ |
代表 低的地块。 |
示例分析:
5 4 1000 2000
. . . #
# . . #
. . . #
# # . .
# # # .
案例图
| . |
. |
. |
# |
| # |
. |
. |
# |
| . |
. |
. |
# |
| # |
# |
. |
. |
| # |
# |
# |
. |
第一步:求出什么都不改变的总花费
只有在不同地块间移动才花费,每次花费A
通过遍历,每当与相邻地块不同时即总费+A
第二步:找到使得花费最小的改变的地块
由于每次的花费都是由于该地块与其四周地块高度不同导致的,所以如果改变某地块高度后,使其与周围不同的地块
数量减小最大,即减小了花费,所以目的是找出改变前与四周地块不同数量最多的地块
第三步:确定最小花费的改造方法
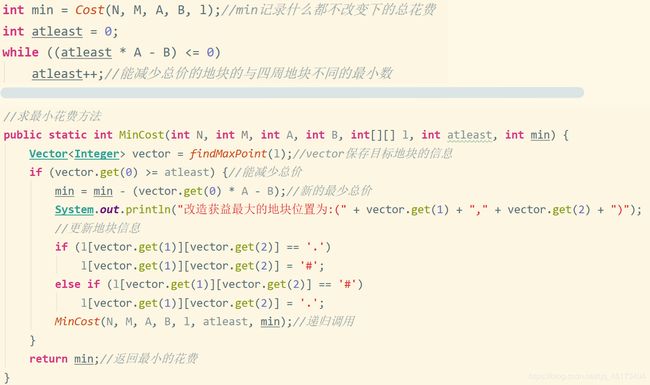
几个变量:
第四步:完整代码
|
|
package 程序艺术方法实验; import java.util.Scanner; import java.util.Vector;
// F 邻家割草 public class Cutgrass { //主函数 public static void main(String[] args) { int N, M, A, B; Scanner scanner = new Scanner(System.in); N = scanner.nextInt(); M = scanner.nextInt(); A = scanner.nextInt(); B = scanner.nextInt(); int l[][] = new int[N][M]; for (int i = 0; i < N; i++) { for (int j = 0; j < M; j++) { l[i][j] = scanner.next().charAt(0); } } int min = Cost(N, M, A, B, l);//min记录什么都不改变下的总花费 int atleast = 0; while ((atleast * A - B) <= 0) atleast++;//能减少总价的地块的与四周地块不同的最小数 System.out.println("最低价格为:" + MinCost(N, M, A, B, l, atleast, min)); }
//什么都不改变的总花费 public static int Cost(int N, int M, int A, int B, int[][] l) { int sum = 0; for (int i = 0; i < N; i++) {//行 for (int j = 0; j < M - 1; j++) {//列 if (l[i][j] != l[i][j + 1]) sum += A; } } for (int i = 0; i < M; i++) {//列 for (int j = 0; j < N - 1; j++) //行 { if (l[j][i] != l[j + 1][i]) sum += A; }
} return sum; }
//找到使得花费最小的改变的地块 public static Vector<Integer> findMaxPoint(int l[][]) { int max = 0;//记录与四周地块不同的最大数量 int p[][] = new int[l.length][l[0].length];//保存每个地块与周围地块不同数量的数组 Vector<Integer> vector = new Vector<>();//保存目标地块的信息 //找每个地块上下左右与自己不同的地块数量 for (int i = 0; i < l.length; i++) { for (int j = 0; j < l[0].length; j++) { int temp = 0;//记录与周围地块不同的数量 if (i + 1 < l.length && l[i][j] != l[i + 1][j])//右边 temp++; if (i - 1 >= 0 && l[i][j] != l[i - 1][j])//左边 temp++; if (j + 1 < l[0].length && l[i][j] != l[i][j + 1])//上边 temp++; if (j - 1 >= 0 && l[i][j] != l[i][j - 1])//下边 temp++; p[i][j] = temp; if (temp > max) max = temp;//得到最大值 } } vector.add(max);//记录目标地块与四周地块不同的数量 for (int i = 0; i < l.length; i++) { for (int j = 0; j < l[0].length; j++) { if (p[i][j] == max) { vector.add(i);//记录目标地块的位置 vector.add(j); break; } } } return vector; }
//求最小花费方法 public static int MinCost(int N, int M, int A, int B, int[][] l, int atleast, int min) { Vector<Integer> vector = findMaxPoint(l);//vector保存目标地块的信息 if (vector.get(0) >= atleast) {//能减少总价 min = min - (vector.get(0) * A - B);//新的最少总价 System.out.println("改造获益最大的地块位置为:(" + vector.get(1) + "," + vector.get(2) + ")"); //更新地块信息 if (l[vector.get(1)][vector.get(2)] == '.') l[vector.get(1)][vector.get(2)] = '#'; else if (l[vector.get(1)][vector.get(2)] == '#') l[vector.get(1)][vector.get(2)] = '.'; MinCost(N, M, A, B, l, atleast, min);//递归调用 } return min;//返回最小的花费 } } |