LeetCode 常见二叉树问题 (python实现)
递归
树是一种常用递归操作的数据结构。一棵树要么是空,要么有两个指针,指向另外两棵树。
1. 树的高度
Leet Code 104. Maximun Depth of Binary Tree (Easy)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if root == None: return 0
return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
2. 平衡树(AVL)
LeetCode 110. Balanced BInary Tree (Easy)
平衡二叉树的判断,是进一步对数的高度的计算。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.result = True
def isBalanced(self, root: TreeNode) -> bool:
self.maxDepth(root)
return self.result
def maxDepth(self, root):
if not root: return 0
lD = self.maxDepth(root.left)
rD = self.maxDepth(root.right)
if abs(lD - rD) > 1: self.result = False
return 1 + max(lD, rD)
3. 树上两节点的最长路径
LeetCode 543. Diameter of Binary Tree (Easy)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.subDepth = 0
def diameterOfBinaryTree(self, root: TreeNode) -> int:
self.calSubDepth(root)
return self.subDepth
def calSubDepth(self, root):
if not root: return 0
leftD = self.calSubDepth(root.left)
rightD = self.calSubDepth(root.right)
self.subDepth = max(self.subDepth, leftD + rightD)
return max(leftD, rightD) + 1
4. 翻转树
LeetCode 226. Invert Binary Tree (Easy)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root: return None
left = root.left
root.left = self.invertTree(root.right)
root.right = self.invertTree(left)
return root
5. 归并两棵树
LeetCode 617. Merge Two Binary Trees (Easy)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
if not t1: return t2
if not t2: return t1
if not t1 and not t2: return None
t1.val += t2.val
t1.left = self.mergeTrees(t1.left, t2.left)
t1.right = self.mergeTrees(t1.right, t2.right)
return t1
6. 判断路径和是否等于一个数
LeetCode 112. Path Sum (Easy)
题目中的加法,在递归过程中被转换成了减法,随着递归的进行,最后比较叶节点的值就可以判断是否存在Sum了。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
if not root: return False
if not root.left and not root.right and root.val == sum: return True
return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)
7. 统计路径和为给定值的路径数量
LeetCode 437. Path Sum III
两个函数互相递归调用。
与6不同的是:6可以从根节点开始就对下一次递归进行sum减法操作。而本题,在进行下一层节点的递归时候,不可以改变sum的值。可以考虑为下一层节点为根节点。相当于遍历每一个节点的时候,都是一次问题6的操作。只是pathSumStartWithRoot()的退出条件不是叶节点,而是空节点。这里res用来记录遍历过程中的结果。
此题需要慢慢理解,两个递归函数是如何协调作用的。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: TreeNode, sum: int) -> int:
if not root: return 0
res = self.pathSumStartWithRoot(root, sum) + self.pathSum(root.left, sum) + self.pathSum(root.right, sum)
return res
def pathSumStartWithRoot(self, root, sum):
if not root: return 0
res = 0
if root.val == sum: res += 1
res += self.pathSumStartWithRoot(root.left, sum - root.val) + self.pathSumStartWithRoot(root.right, sum - root.val)
return res
8. 子树
LeetCode 572. Subtree of Another Tree
整体思路和上一题很像。区别在于上一题是数字的计算,本题是布尔值的判断
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSubtree(self, s: TreeNode, t: TreeNode) -> bool:
if not s: return False
return self.sameJudge(s, t) or self.isSubtree(s.left, t) or self.isSubtree(s.right, t)
def sameJudge(self, s, t):
if not s and not t: return True
if not s or not t: return False
if s.val != t.val: return False
return self.sameJudge(s.left, t.left) and self.sameJudge(s.right, t.right)
9. 树的对称
LeetCode 101. Symmetric Tree (Easy)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root: return True
return self.subTreeJudge(root.left, root.right)
def subTreeJudge(self, t1, t2):
if not t1 and not t2: return True
if not t1 or not t2: return False
if t1.val != t2.val: return False
return self.subTreeJudge(t1.left, t2.right) and self.subTreeJudge(t1.right, t2.left)
10. 最小路径
LeetCode 111. Minimum Depth of Binary Tree(Easy)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root: return 0
left = self.minDepth(root.left)
right = self.minDepth(root.right)
# 当左右子树一个为空时候,深度为另一课数的深度+1
if left == 0 or right == 0: return left + right + 1
# 当两子树都不为空的时候,返回潜的那棵树长度+1
return min(left, right) + 1
11. 统计左叶节点值的和
LeetCode 404. Sum of Left Leaves (Easy)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root: TreeNode) -> int:
if not root: return 0
if self.isLeave(root.left): return root.left.val + self.sumOfLeftLeaves(root.right)
return self.sumOfLeftLeaves(root.left) + self.sumOfLeftLeaves(root.right)
def isLeave(self, root):
if not root: return False
if not root.left and not root.right: return True
12. 相同节点值的最大路径长度
LeetCode 687. Longest Univalue Path (Easy)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.length = 0
def longestUnivaluePath(self, root: TreeNode) -> int:
self.dfs(root)
return self.length
def dfs(self, root):
if not root: return 0
left = self.dfs(root.left)
right = self.dfs(root.right)
left_len = left + 1 if root.left and root.left.val == root.val else 0
right_len = right + 1 if root.right and root.right.val == root.val else 0
self.length = max(self.length, left_len + right_len)
return max(left_len, right_len)
13. 间隔遍历
LeetCode 337. House Robber III (Medium)
# 此方法Time Out,超时的原因应该是,一个函数内部竟然需要调用6次递归函数。
# 通过添加字典记录已经计算过的节点,节省运算时间
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.history = {}
def rob(self, root: TreeNode) -> int:
if not root: return 0
if root in self.history:
return self.history[root]
total1 = root.val
if root.left:
total1 += self.rob(root.left.left) + self.rob(root.left.right)
if root.right:
total1 += self.rob(root.right.left) + self.rob(root.right.right)
total2 = self.rob(root.left) + self.rob(root.right)
res = max(total1, total2)
self.history[root] = res
return res
# 下面方法和上面思路有一点小差异,递归函数返回三个值,(当前节点值,左孩子节点值,右孩子节点值)
# (root.left节点的值, root.left.left节点值, root.left.right节点值)
class Solution:
def rob(self, root: TreeNode) -> int:
return self.myrob(root)[0]
def myrob(self, root):
if not root: return 0, 0, 0
l, ll, lr = self.myrob(root.left)
r, rl, rr = self.myrob(root.right)
# 第一个返回值很好理解,后面两个l, r不太容易理解,这里由于函数向上一层返回,即本层节点的左孩子l一定是上层函数的ll, 本层节点的r, 一定是上层函数的lr
return max(root.val + ll + lr + rl + rr, l + r), l, r
14. 找出二叉树中第二小的节点
LeetCode 671. Second Minimum Node In a Binary Tree (Easy)
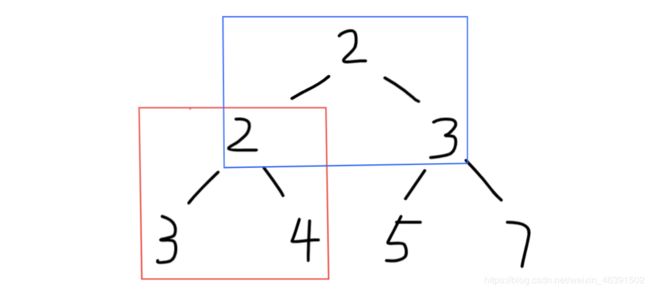
考虑上图二叉树。由于该题目的特性可知:父节点总是小于等于孩子节点。如果不考虑等于的情况最小值一定出现在父节点上(如红色框框所示)。那么第二小的值一定出现在左右孩子中的一个。可能是左孩子的值,也可能是右孩子的值。也可能是-1.
那么考虑最简单的树,红色框框的树。如果父节点和子节点值都不同,那么第二小的值一定是子节点中值较小的那个。如果父节点和其中一个子节点值相同(假设是左子节点,如蓝色框框所示)。由于父节点一般记录的是最小的值,现在左子节点与其相同了,那么第二小的节点就可能存在于左子树中,这时候递归左子树去寻找该值。同理递归右子树。
最终3中情况返回:
- 如果左右孩子节点均有子树,返回左右孩子节点中较小的那个值即整棵树第二小的值(红色框框的情形)
- 如果左孩子没子树,则返回左孩子节点的值
- 否则返回右孩子节点的值
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
if not root: return -1
if not root.left and not root.right: return -1
left = root.left.val
right = root.right.val
# if value same as root val, need to find the next candidate
if root.left.val == root.val:
left = self.findSecondMinimumValue(root.left)
if root.right.val == root.val:
right = self.findSecondMinimumValue(root.right)
if left != -1 and right != -1:
return min(left, right)
elif left != -1:
return left
else:
return right
层次遍历
层次遍历是图的一种广度优先搜索。BFS。需要使用队列数据结构来辅助搜索过程。
1. 一棵树每层节点的平均数
LeetCode 637. Average of Levels in Binary Tree(Easy)
每层节点需要在队列中间插入一个hint信息。隔离层与层之间的数据。这里使用end作为hint标记。当end出队列的时候,意味着前一层节点全部遍历完毕,那么当前队头到队尾的均为下一层的节点。此时在队的末尾再添加一个end标记,用以隔离下一层元素。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def averageOfLevels(self, root: TreeNode) -> List[float]:
Q = [root]
Q.append('end')
res = []
sum, n = 0, 0
while Q:
if Q[0] != 'end':
sum += Q[0].val
n += 1
if Q[0].left: Q.append(Q[0].left)
if Q[0].right: Q.append(Q[0].right)
del Q[0]
else:
res.append(sum/n)
del Q[0]
if not Q: break
Q.append('end')
sum, n = 0, 0
return res
2. 得到左下角的节点值
LeetCode 513. Find Bottom Left Tree Value(Easy)
层次遍历先访问右子树再访问左子树,得到的最后一个结果就是所求结果。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findBottomLeftValue(self, root: TreeNode) -> int:
Q = []
Q.append(root)
while Q:
res = Q[0].val
if Q[0].right: Q.append(Q[0].right)
if Q[0].left: Q.append(Q[0].left)
del Q[0]
return res
前序、中序、后续遍历
前序遍历
def preOrder(root):
if not root: return
visit(root.val)
preOrder(root.left)
preOrder(root.right)
中序遍历
def inOrder(root):
if not root: return
inOrder(root.left)
visit(root.val)
inOrder(root.right)
后序遍历
def postOrder(root):
if not root: return
postOrder(root.left)
postOrder(root.right)
visit(root.val)
1. 非递归实现二叉树的前序遍历
LeetCode 144. Binary Tree Preorder Traversal (Medium)
二叉树的非递归前序遍历,通过借助栈先进后出(FILO)的特性实现。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
if not root: return []
stack, res = [], []
stack.append(root)
while stack:
cur = stack.pop()
res.append(cur.val)
if cur.right: stack.append(cur.right)
if cur.left: stack.append(cur.left)
return res
2. 非递归实现二叉树的后序遍历
LeetCode 145. Binary Tree Postorder Traversal (Hard)
前序遍历顺序为:root -> left -> right,后序遍历顺序为:left -> right -> root。非递归实现后续遍历,有一个小技巧。如果将前序遍历改成root -> right -> left,那么逆序这个遍历顺序,就是后序遍历。
如果不使用这个小技巧的方法,我还不知道。。。哈哈
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if not root: return []
stack, res = [], []
stack.append(root)
while stack:
cur = stack.pop()
res.append(cur.val)
if cur.left: stack.append(cur.left)
if cur.right: stack.append(cur.right)
return reversed(res)
3. 非递归实现二叉树的中序遍历
LeetCode 97. Binary Tree Inorder Traversal (Medium)
实现思路:如果当前节点不为空,或者当前栈不空,当前节点入栈,当前节点指向其左子树位置(寻找数的最左边节点)。从栈中依次弹出一个节点进行访问,并将当前节点指向其右子树的位置,循环进行。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
if not root: return []
stack, res = [], []
current = root
while current or stack:
while current:
stack.append(current)
current = current.left
node = stack.pop()
res.append(node.val)
current = node.right
return res
BST 二叉搜索树
二叉搜索树的性质:
- 根节点的值大于等于左子树的所有节点值,小于等于右子树的所有节点值
- 二叉搜索树的中序遍历是一个递增序列
1. 修剪二叉搜索树
LeetCode 669. Trim a Binary Search Tree (Easy)
修剪结果无非有三种情形
L < root.val < Rroot.val > Rroot.val < L
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def trimBST(self, root: TreeNode, L: int, R: int) -> TreeNode:
if not root: return
if root.val > R:
root = self.trimBST(root.left, L, R)
elif root.val < L:
root = self.trimBST(root.right, L, R)
else:
root.left = self.trimBST(root.left, L, R)
root.right = self.trimBST(root.right, L, R)
return root
2. 寻找二叉搜索树的第k个元素
中序遍历BST结果是一个升序序列。设置递归函数外的变量记录递归过程即可实现计数第k个元素。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
self.k = k
self.res = 0
self.dfs(root)
return self.res
def dfs(self, root):
if root != None:
self.dfs(root.left)
self.k -= 1
if self.k == 0:
self.res = root.val
self.dfs(root.right)
3. 把二叉搜索树的每个节点的值都加上比他大的节点的值
BST中序遍历是一个升序序列,那么先访问右子树再访问左子树的中序遍历就是一个降序序列。降序序列第一个数的值不停的加到一个sum变量中,以后每次遍历数值都增加该数。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def convertBST(self, root: TreeNode) -> TreeNode:
self.sum = 0
self.dfs(root)
return root
def dfs(self, root):
if not root: return
self.dfs(root.right)
self.sum += root.val
root.val = self.sum
self.dfs(root.left)
4. 二叉树的最近公共祖先(Binary Tree)
LeetCode 236. Lowest Common Ancestor of a Binary Tree
递归总是需要考虑最小子问题的情形!!!这里指的是三个节点的数的一般情况。
每一次递归,都只是对一个最小二层树的判断,没有遇到p或q之前,返回的都是None。因此最后的三个if判断是包括了所有的情形。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if not root: return None
if root == p or root == q: return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if not left: return right
elif not right: return left
else: return root
5. 二叉搜索树的最近公共祖先(Binary Search Tree)
LeetCode 235. Lowest Common Ancestor of a Binary Search Tree (Easy)
遇上一题不同之处在于,这是一个二叉搜索树且没有重复节点。搜索树总是有root.val > root.left, root.val < root.right.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if root.val > p.val and root.val > q.val:
return self.lowestCommonAncestor(root.left, p, q)
if root.val < p.val and root.val < q.val:
return self.lowestCommonAncestor(root.right, p, q)
return root
6. 从有序数组中构造二叉搜索树
LeetCode 108. Convert Sorted Array to Binary Search Tree (Easy)
将有序数组分成三个部分,分别递归构建这三个部分。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
return self.buildBST(nums, 0, len(nums)-1)
def buildBST(self, nums, l, r):
if l > r: return None
m = l + (r - l) // 2
root = TreeNode(nums[m])
root.left = self.buildBST(nums, l, m-1)
root.right = self.buildBST(nums, m+1, r)
return root
7. 根据有序链表构造平衡二叉搜索树
LeetCode 109. Convert Sorted List to Binary Search Tree (Medium)
与上一题是同类型题,这里使用快慢指针方法寻找链表的中间节点。将链表分为三个部分。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedListToBST(self, head: ListNode) -> TreeNode:
if not head: return None
if not head.next: return TreeNode(head.val)
mid = self.findM(head)
root = TreeNode(mid.val)
root.left = self.sortedListToBST(head)
root.right = self.sortedListToBST(mid.next)
return root
def findM(self, head) -> ListNode:
slow = fast = head
prev = None
while fast and fast.next:
prev = slow
slow = slow.next
fast = fast.next.next
prev.next = None
return slow
8. 判断二叉搜索树中是否存在两个节点,使他们和为给定值
中序遍历得到一个单调递增数组,用滑动窗口思想,left,right分别指向列表两段,向中间滑动。依次两段向中间滑动计算两个数的和。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.nums = []
def findTarget(self, root: TreeNode, k: int) -> bool:
self.inOrder(root)
total, left, right = 0, 0, len(self.nums)-1
while left < right:
total = self.nums[left] + self.nums[right]
if total == k: return True
if total < k: left += 1
else: right -= 1
return False
def inOrder(self, root):
if not root: return
self.inOrder(root.left)
self.nums.append(root.val)
self.inOrder(root.right)
9. 在二叉搜索树中查找两个节点之差的最小绝对值
LeetCode 530. Minimum Absolute Difference in BST (Easy)
利用二叉搜索树中序遍历是单调递增序列的性质,在中序遍历过程中,记录prev节点信息,遍历到每一个节点的同时计算与prev节点的差值。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.minimum = float('inf')
self.prev = None
def getMinimumDifference(self, root: TreeNode) -> int:
self.inOrder(root)
return self.minimum
def inOrder(self, root):
if not root: return
self.inOrder(root.left)
if self.prev:
self.minimum = min((root.val - self.prev.val), self.minimum)
self.prev = root
self.inOrder(root.right)
10. 寻找二叉搜索树中出现次数最多的值
LeetCode 501. Find Mode in Binary Search Tree (Easy)
此问题是上一问题的扩展。程序整体框架没有发生过大的改变。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.res = []
self.maxTimes = 1
self.times = 1
self.prev = None
def findMode(self, root: TreeNode) -> List[int]:
self.inOrder(root)
return self.res
def inOrder(self, root):
if not root: return
self.inOrder(root.left)
if self.prev:
if root.val == self.prev.val:
self.times += 1
else:
self.times = 1
if self.times > self.maxTimes:
self.maxTimes = self.times
self.res.clear()
self.res.append(root.val)
elif self.times == self.maxTimes:
self.res.append(root.val)
self.prev = root
self.inOrder(root.right)
Trie 前缀树
前缀树又称为字典树,用于判断字符串是否存在相同前缀
1. 实现一个Trie
这里使用字典来存储前缀树。树的根节点是一个空字典。详细信息可以参考博客文章构建字典树。
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = {}
self.word_end = -1
def insert(self, word: str) -> None:
"""
Inserts a word into the trie.
"""
curNode = self.root
for c in word:
if c not in curNode:
curNode[c] = {}
curNode = curNode[c]
curNode[self.word_end] = True
def search(self, word: str) -> bool:
"""
Returns if the word is in the trie.
"""
curNode = self.root
for c in word:
if c not in curNode:
return False
curNode = curNode[c]
# Check if curNode has end flag now.
if self.word_end not in curNode:
return False
return True
def startsWith(self, prefix: str) -> bool:
"""
Returns if there is any word in the trie that starts with the given prefix.
"""
curNode = self.root
for c in prefix:
if c not in curNode:
return False
curNode = curNode[c]
return True
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)
2. 实现一个前缀Trie,求前缀和
创建两个字典,一个用来存储字典形式的前缀树,一个用来存储该字符串key是否已经存在。
# Runtime: 16ms
# Memory Usage: 13.8MB
class MapSum:
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = {}
self.history = {}
def insert(self, key: str, val: int) -> None:
curr = self.root
if key not in self.history:
self.history[key] = val
for ch in key:
if ch not in curr:
curr[ch] = {'time': val}
else:
curr[ch]['time'] += val
curr = curr[ch]
else:
for ch in key:
curr[ch]['time'] += (val - self.history[key])
curr = curr[ch]
# 任何一个字符不存在都返回0值
def sum(self, prefix: str) -> int:
curr = self.root
for ch in prefix:
if ch not in curr:
return 0
else:
curr = curr[ch]
return curr['time']