原文链接:http://tecdat.cn/?p=13913
我们讨论了使用程序来获得预测的置信区间的方法。我们将讨论线性回归。
> plot(cars)
> reg=lm(dist~speed,data=cars)
> abline(reg,col="red")
> n=nrow(cars)
> x=21
> points(x,predict(reg,newdata= data.frame(speed=x)),pch=19,col="red")
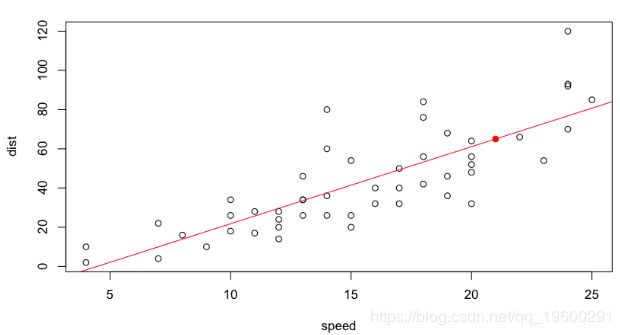
我们正在这里做出一个预测。正如在R课堂上（以及在预测模型的过程中）所回顾的，当我们要为预测提供一个置信区间时，建议您为预测器确定置信区间（这将取决于预测误差）参数的估计）和潜在值的置信区间（这也取决于模型误差，即残差的离散度）。让我们从预测的置信区间开始:
abline(reg,col="light blue")
points(x,predict(reg,newdata=data.frame(speed=x)),pch=19,col="blue")
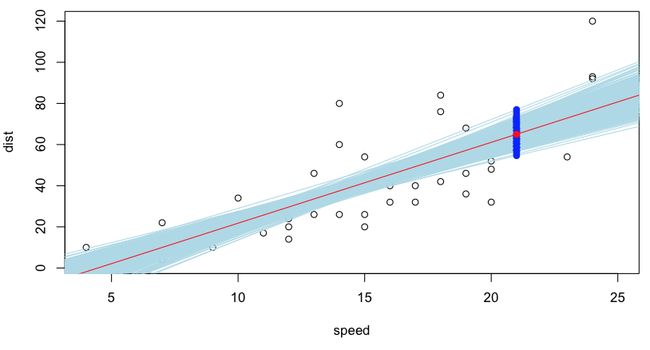
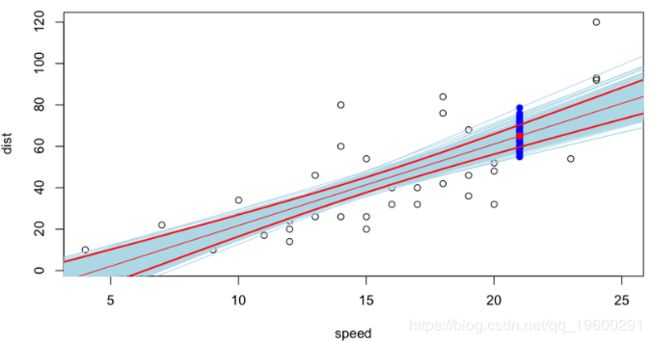
蓝色值是可能的预测，可以通过在我们的观察数据库中重新采样获得。残差（以及因此的斜率和回归线的常数的估计值）的正态性假设下的置信区间（为90％）如下
lines(0:30,U[,2],col="red",lwd=2)
lines(0:30,U[,3],col="red",lwd=2)
我们可以在这里比较在500个生成的数据集上获得的值的分布，并比较经验分位数和假设正态性下的分位数，
polygon(c(D$x[I],rev(D$x[I])),c(D$y[I],rep(0,length(I))),col="blue",border=NA)
数量比较
5% 95%
58.63689 70.31281
fit lwr upr
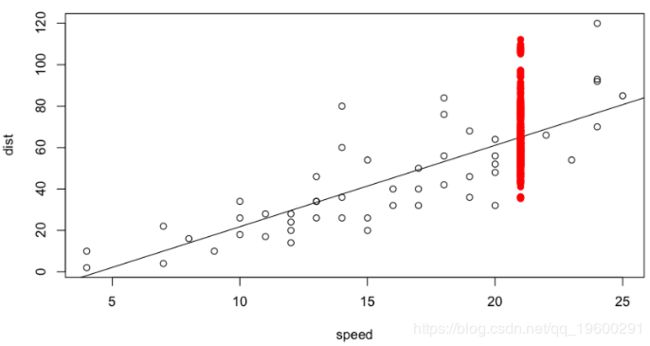
65.00149 59.65934 70.34364现在，让我们来看另一种类型的置信区间，即关注变量的可能值。这次，除了绘制新样本和计算预测值之外，我们还将在每次绘制中添加噪声，我们获得可能的值。
points(x,Yx[s],pch=19,col="red")
同样，在这里，我们可以比较（以图形方式开始）通过重采样获得的值，以及在正常情况下获得的值，
polygon(c(D$x[I],rev(D$x[I])),c(D$y[I],rep(0,length(I))),col="blue",border=NA)
从数字上给出以下比较
5% 95%
44.43468 96.01357
fit lwr upr
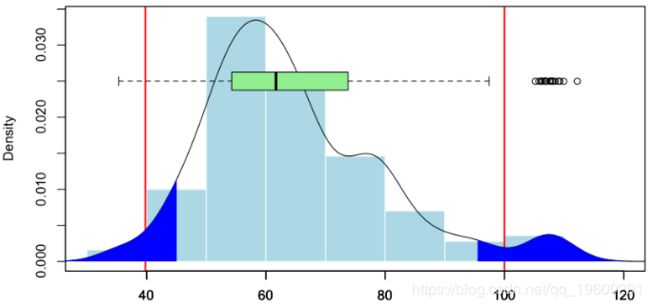
1 67.63136 45.16967 90.09305这次右侧略有不对称。显然，我们不能假设高斯残差，因为正值比负值大。考虑到数据的性质（距离不能为负），这是合理的。
然后，我们开始讨论使用回归模型。
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 3209 4372 4411 4428 4435 4456
[2,] 3367 4659 4696 4720 4730 NA
[3,] 3871 5345 5398 5420 NA NA
[4,] 4239 5917 6020 NA NA NA
[5,] 4929 6794 NA NA NA NA
[6,] 5217 NA NA NA NA NA
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 3209 1163 39 17 7 21
[2,] 3367 1292 37 24 10 NA
[3,] 3871 1474 53 22 NA NA
[4,] 4239 1678 103 NA NA NA
[5,] 4929 1865 NA NA NA NA
[6,] 5217 NA NA NA NA NA然后，我们可以建立一个数据。
> head(base,12)
y ai bj
1 3209 2000 0
2 3367 2001 0
3 3871 2002 0
4 4239 2003 0
5 4929 2004 0
6 5217 2005 0
7 1163 2000 1
8 1292 2001 1
9 1474 2002 1
10 1678 2003 1
11 1865 2004 1
12 NA 2005 1
> tail(base,12)
y ai bj
25 7 2000 4
26 10 2001 4
27 NA 2002 4
28 NA 2003 4
29 NA 2004 4
30 NA 2005 4
31 21 2000 5
32 NA 2001 5
33 NA 2002 5
34 NA 2003 5
35 NA 2004 5
36 NA 2005 5然后，我们可以使用基于 Stavros Christofides的对数增量支付模型的回归模型，该模型基于对数正态模型，该模型最初由Etienne de Vylder于1978年提出。
Residuals:
Min 1Q Median 3Q Max
-0.26374 -0.05681 0.00000 0.04419 0.33014
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.9471 0.1101 72.188 6.35e-15 ***
as.factor(ai)2001 0.1604 0.1109 1.447 0.17849
as.factor(ai)2002 0.2718 0.1208 2.250 0.04819 *
as.factor(ai)2003 0.5904 0.1342 4.399 0.00134 **
as.factor(ai)2004 0.5535 0.1562 3.543 0.00533 **
as.factor(ai)2005 0.6126 0.2070 2.959 0.01431 *
as.factor(bj)1 -0.9674 0.1109 -8.726 5.46e-06 ***
as.factor(bj)2 -4.2329 0.1208 -35.038 8.50e-12 ***
as.factor(bj)3 -5.0571 0.1342 -37.684 4.13e-12 ***
as.factor(bj)4 -5.9031 0.1562 -37.783 4.02e-12 ***
as.factor(bj)5 -4.9026 0.2070 -23.685 4.08e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1753 on 10 degrees of freedom
(15 observations deleted due to missingness)
Multiple R-squared: 0.9975, Adjusted R-squared: 0.9949
F-statistic: 391.7 on 10 and 10 DF, p-value: 1.338e-11
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 2871.2 1091.3 41.7 18.3 7.8 21.3
[2,] 3370.8 1281.2 48.9 21.5 9.2 25.0
[3,] 3768.0 1432.1 54.7 24.0 10.3 28.0
[4,] 5181.5 1969.4 75.2 33.0 14.2 38.5
[5,] 4994.1 1898.1 72.5 31.8 13.6 37.1
[6,] 5297.8 2013.6 76.9 33.7 14.5 39.3
> sum(base$py[is.na(base$y)])
[1] 2481.857我们获得与通过Chain Ladder方法获得的结果略有不同。如Hachemeister和Stanard在1975年所建议的，我们还可以尝试Poisson回归（具有对数链接），
Deviance Residuals:
Min 1Q Median 3Q Max
-2.3426 -0.4996 0.0000 0.2770 3.9355
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 8.05697 0.01551 519.426 < 2e-16 ***
as.factor(ai)2001 0.06440 0.02090 3.081 0.00206 **
as.factor(ai)2002 0.20242 0.02025 9.995 < 2e-16 ***
as.factor(ai)2003 0.31175 0.01980 15.744 < 2e-16 ***
as.factor(ai)2004 0.44407 0.01933 22.971 < 2e-16 ***
as.factor(ai)2005 0.50271 0.02079 24.179 < 2e-16 ***
as.factor(bj)1 -0.96513 0.01359 -70.994 < 2e-16 ***
as.factor(bj)2 -4.14853 0.06613 -62.729 < 2e-16 ***
as.factor(bj)3 -5.10499 0.12632 -40.413 < 2e-16 ***
as.factor(bj)4 -5.94962 0.24279 -24.505 < 2e-16 ***
as.factor(bj)5 -5.01244 0.21877 -22.912 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 46695.269 on 20 degrees of freedom
Residual deviance: 30.214 on 10 degrees of freedom
(15 observations deleted due to missingness)
AIC: 209.52
Number of Fisher Scoring iterations: 4
> round(matrix(base$py2,n,n),1)
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 3155.7 1202.1 49.8 19.1 8.2 21.0
[2,] 3365.6 1282.1 53.1 20.4 8.8 22.4
[3,] 3863.7 1471.8 61.0 23.4 10.1 25.7
[4,] 4310.1 1641.9 68.0 26.1 11.2 28.7
[5,] 4919.9 1874.1 77.7 29.8 12.8 32.7
[6,] 5217.0 1987.3 82.4 31.6 13.6 34.7
>
> sum(base$py2[is.na(base$y)])
[1] 2426.985该预测与通过链梯方法获得的估计量一致。Klaus Schmidt和AngelaWünsche于1998年在链梯，边际总和和最大似然估计中建立了带有最小偏差方法的链接。