数据结构课程设计(九)---公交线路提示
1、任务简述:
上网下载真实南京公交线路图,建立南京主要公交线路图的存储结构
要求:
(1)输入任意两站点,给出转车次数最少的乘车路线。
(2)输入任意两站点,给出经过站点最少的乘车路线。
(3)加分项:可以输出全部符合要求的乘车路线
2、算法描述:
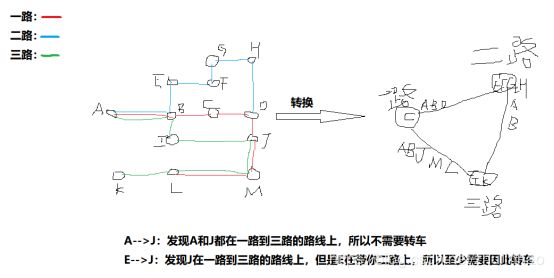
站与站之间的图直接读取文件即可得到。而最小换乘需要一张车与车之间的图。在原本的站与站的图里,我在邻接表里存储了车的信息(可以知道每一条弧是哪一路车上的),可以方便后来构造车与车的图
最短路径算法:
未使用dijkstra算法而通过改进广度优先搜索来实现最短路径。
因为不论是站与站之间的图还是车与车之间的图,每一个结点之间权值都是1,将其联想到广度优先里一层一层搜索的思路。因为搜索完一层才会搜索下一层,所以最先搜索到终点的那一层肯定是最小层数(最少战点或最少换乘),肯定可以反向往上层查找找出一条最短路径。
实现方法是运用广度优先搜索里的visited数组,不用其表示是否访问过,而用其存储层数。广度搜索中队列每弹出一个站点,就搜索所有和该站点相邻的结点,如果未访问,就visited中置为1,表示访问过,然后进队列。这里改进为,visited置为当前层数+1。如果找到了终点,就结束广度搜索,并且用栈配合visited数组一层一层的往上找,最后将全部出栈,得出的就是一条最短路径。
#include 4、运行结果
原始数据:



输入非法数据:

输入相同的合法数据:
5、总结
心得体会:
运行结果正确,不过该题难度较大,相比dijkstra对每一个点每一次循环都对每个点进行更新,广度搜索每个点只访问一次。缺点是由于数据结构的问题,我如果要在最少换乘输出在哪一站换乘会相对麻烦。或许在从站与站的图到车与车的图转换时,可以把中转点记录到邻接表中。
遇到问题和解决方法:
如果你们仔细看我的代码,你们会发现我只用了宽搜,没有用深搜,因为如果一条一条的遍历过去,那么实在是他花时间了,所以,我想出了一个新的思路: