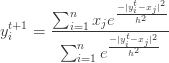运动目标跟踪（四）--搜索算法优化搜索方向之Camshift

mean-shift 的特点是把支撑空间和特征空间在数据密度的框架下综合了起来。对图像来讲，支撑空间就是像素点的坐标，特征空间就是对应像素点的灰度或者RGB三分量。将这两个空间综合后，一个数据点就是一个5维的向量：[x,y,r,g,b]。

这在观念上看似简单，实质是一个飞跃，它是mean-shift方法的基点。

mean-shift方法很宝贵的一个特点就是在这样迭代计算的框架下，求得的mean-shift向量必收敛于数据密度的局部最大点。可以细看[ComaniciuMeer2002]的文章。

写了点程序，可以对图像做简单的mean-shift filtering，供参考：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [DRGB, DSD, MSSD] = MScut(sMode, RGB_raw, hs, hf, m );
% designed for segmenting a colour image using mean-shift [ComaniciuMeer 2002]
% image must be color
% procedure in mean-shift
% 1. combine support space and feature space to make a mean-shift space
% based data description
% 2. for every mean-shift space data
% 3. do mean-shift filtering
%    until convergence
% 4. end
% 5. find the converged mean-shift space data that you are interested in
% and label it
% 6. repeat the above steps
%
% a    -- data in support space
% b    -- data in feature space
% x    -- data in mean-shift space
% f(.)  -- data density function
% k(.)  -- profile function (implicit)
% g(.)  -- profile function (explicit)
% m    -- mean shift vector
% hs -- bandwidth in support space
% hf -- bandwidth in feature space
% M    -- threshold to make a distinct cluster
%% enter $hs$, $hf$, $m$ if necessary
if ~exist('hs')
hs = input('please enter spatial bandwidth (hs):\n');
end
if ~exist('hf')
hf = input('please enter feature bandwidth (hf):\n');
end
if ~exist('m')
m = input('please enter minimum cluster size (m):\n');
end
switch upper(sMode)
case 'RGB'
      RGB = double( RGB_raw );
case 'gray'
      error('FCMcut must use colored image to do segmentation!')
end
sz = size(RGB);
mTCUT = Tcut( RGB(:,:,1) ); % trivial segmentation

%% project data into mean-shift space to make $MSSD$ (mean-shift space data)
mT = repmat([1:sz(1)]', 1, sz(2));
vX = mT(1:end)';          % row
mT = repmat([1:sz(2)], sz(1), 1);
vY = mT(1:end)';  % column
mT = RGB(:,:,1);
vR = mT(1:end)'; % red
mT = RGB(:,:,2);
vG = mT(1:end)'; % green
mT = RGB(:,:,3);
vB = mT(1:end)'; % blue
MSSD = [vX, vY, vR, vG, vB];
%% make $g$ - explicit profile function
disp('Using flat kernel: Epanechnikov kernel...')
g_s = ones(2*hs+1, 2); % 's' for support space
g_f = ones(2*hf+1, 3); % 'f' for feature space
%% main part $$
nIteration = 4;
nData = length(MSSD); % total number of data
DSD    = MSSD*0; % 'DSD' for destination space data
for k = 1:nData
%
tMSSD = MSSD(k,:); % 't' for temp
for l = 1:nIteration
      %
      mT = abs( MSSD - repmat(tMSSD, nData, 1));
      vT = logical( (mT(:,1)<=hs).*(mT(:,2)<=hs).*(mT(:,3)<=hf).*(mT(:,4)<=hf).*(mT(:,5)<=hf) );
      v  = MSSD(vT,:);
      % update $tMSSD$
      tMSSD = mean( v, 1 );
      if nIteration == l
         DSD(k,:) = tMSSD;
      end
end
end
% show result
DRGB = RGB * 0;
DRGB(:,:,1) = reshape(DSD(:,3), sz(1), sz(2)); % red
DRGB(:,:,2) = reshape(DSD(:,4), sz(1), sz(2)); % red
DRGB(:,:,3) = reshape(DSD(:,5), sz(1), sz(2)); % red

figure, imshow(uint8(DRGB), [])

OpenCV实现的mean shift filtering/segmentation解析

(2013-04-13 22:19:49)

Mean shift作为一种有效地特征空间分析方法，在图像滤波，图像分割，物体跟踪等方面都有广泛的应用。
Mean shift算法的详细介绍，可以参见PAMI 2002的paper。
Comaniciu, D. and P. Meer (2002). "Mean shift: A robust approach toward feature space analysis." Pattern Analysis and Machine Intelligence, IEEE Transactions on 24(5): 603-619.

OpenCV分别实现了mean shift用来做跟踪、分割和滤波的函数。
其中滤波的c++函数原型为：
void pyrMeanShiftFiltering(InputArray src, OutputArray dst, double sp, double sr, int maxLevel=1, TermCriteria termcrit=TermCriteria( TermCriteria::MAX_ITER+TermCriteria::EPS,5,1) )
src和dst分别为输入和输出图像，8 bit,3 channel,sp和sr为空间域和颜色域的半径，maxLevel为分割用金字塔的最大层数，termcrit为迭代的终止条件。

跟踪的函数原型为：
int meanShift(InputArray probImage, Rect& window, TermCriteria criteria)
proImage为生成的物体存在的概率图，window为初始化的搜索窗口（同时是输出的搜索结果），criteria为终止条件。

分割的函数原型为：
void gpu:: meanShiftSegmentation(const GpuMat& src, Mat& dst, int sp, int sr, int minsize, TermCriteria criteria=TermCriteria(TermCriteria::MAX_ITER + TermCriteria::EPS, 5, 1))
大部分参数与 pyrMeanShiftFiltering相同，minsize为最小的分割区域大小，小于这个大小的区域会被合并。

OpenCV sample里用pyrMeanShiftFiltering和floodfill函数共同实现了简单的分割的例子.（/samples/cpp/Meanshift_segmentation.cpp）。

Mean Shift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,移动该点到其偏移均值,然后以此为新的起始点,继续移动,直到满足一定的条件结束.

1. Meanshift推导

给定d维空间Rd的n个样本点 ,i=1,…,n,在空间中任选一点x，那么Mean Shift向量的基本形式定义为:

Sk是一个半径为h的高维球区域,满足以下关系的y点的集合,

k表示在这n个样本点xi中,有k个点落入Sk区域中.

以上是官方的说法，即书上的定义，我的理解就是，在d维空间中，任选一个点，然后以这个点为圆心，h为半径做一个高维球，因为有d维，d可能大于2，所以是高维球。落在这个球内的所有点和圆心都会产生一个向量，向量是以圆心为起点落在球内的点位终点。然后把这些向量都相加。相加的结果就是Meanshift向量。

如图所以。其中黄色箭头就是Mh（meanshift向量）。

再以meanshift向量的终点为圆心，再做一个高维的球。如下图所以，重复以上步骤，就可得到一个meanshift向量。如此重复下去，meanshift算法可以收敛到概率密度最大得地方。也就是最稠密的地方。

最终的结果如下：

Meanshift推导：

把基本的meanshift向量加入核函数，核函数的性质在这篇博客介绍：http://www.cnblogs.com/liqizhou/archive/2012/05/11/2495788.html

那么，meanshift算法变形为

(1)

解释一下K()核函数，h为半径，Ck,d/nhd 为单位密度，要使得上式f得到最大，最容易想到的就是对上式进行求导，的确meanshift就是对上式进行求导.

(2)

令：

K(x)叫做g(x)的影子核，名字听上去听深奥的，也就是求导的负方向，那么上式可以表示

对于上式，如果才用高斯核，那么，第一项就等于fh,k

第二项就相当于一个meanshift向量的式子：

那么（2）就可以表示为

下图分析的构成，如图所以，可以很清晰的表达其构成。

要使得=0，当且仅当=0，可以得出新的圆心坐标：

（3）

上面介绍了meanshift的流程，但是比较散，下面具体给出它的算法流程。

选择空间中x为圆心，以h为半径为半径，做一个高维球，落在所有球内的所有点xi
计算，如果<ε(人工设定)，推出程序。如果>ε, 则利用（3）计算x，返回1.

2.meanshift在图像上的聚类：

真正大牛的人就能创造算法，例如像meanshift，em这个样的算法，这样的创新才能推动整个学科的发展。还有的人就是把算法运用的实际的运用中，推动整个工业进步，也就是技术的进步。下面介绍meashift算法怎样运用到图像上的聚类核跟踪。

一般一个图像就是个矩阵，像素点均匀的分布在图像上，就没有点的稠密性。所以怎样来定义点的概率密度，这才是最关键的。

如果我们就算点x的概率密度，采用的方法如下：以x为圆心，以h为半径。落在球内的点位xi 定义二个模式规则。

（1）x像素点的颜色与xi像素点颜色越相近，我们定义概率密度越高。

（2）离x的位置越近的像素点xi，定义概率密度越高。

所以定义总的概率密度，是二个规则概率密度乘积的结果，可以（4）表示

（4）

其中：代表空间位置的信息，离远点越近，其值就越大，表示颜色信息，颜色越相似，其值越大。如图左上角图片，按照（4）计算的概率密度如图右上。利用meanshift对其聚类，可得到左下角的图。

Camshift算法原理及其Opencv实现

Camshift原理
camshift利用目标的颜色直方图模型将图像转换为颜色概率分布图，初始化一个搜索窗的大小和位置，并根据上一帧得到的结果自适应调整搜索窗口的位置和大小，从而定位出当前图像中目标的中心位置。

分为三个部分：
1--色彩投影图（反向投影）：
(1).RGB颜色空间对光照亮度变化较为敏感，为了减少此变化对跟踪效果的影响，首先将图像从RGB空间转换到HSV空间。(2).然后对其中的H分量作直方图，在直方图中代表了不同H分量值出现的概率或者像素个数，就是说可以查找出H分量大小为h的概率或者像素个数，即得到了颜色概率查找表。(3).将图像中每个像素的值用其颜色出现的概率对替换，就得到了颜色概率分布图。这个过程就叫反向投影，颜色概率分布图是一个灰度图像。

2--meanshift
meanshift算法是一种密度函数梯度估计的非参数方法，通过迭代寻优找到概率分布的极值来定位目标。
算法过程为：
(1).在颜色概率分布图中选取搜索窗W
(2).计算零阶距：

计算一阶距：

计算搜索窗的质心：

(3).调整搜索窗大小
宽度为；长度为1.2s；
(4).移动搜索窗的中心到质心，如果移动距离大于预设的固定阈值，则重复2)3)4)，直到搜索窗的中心与质心间的移动距离小于预设的固定阈值，或者循环运算的次数达到某一最大值，停止计算。关于meanshift的收敛性证明可以google相关文献。

3--camshift
将meanshift算法扩展到连续图像序列，就是camshift算法。它将视频的所有帧做meanshift运算，并将上一帧的结果，即搜索窗的大小和中心，作为下一帧meanshift算法搜索窗的初始值。如此迭代下去，就可以实现对目标的跟踪。
算法过程为：
(1).初始化搜索窗
(2).计算搜索窗的颜色概率分布（反向投影）
(3).运行meanshift算法，获得搜索窗新的大小和位置。
(4).在下一帧视频图像中用(3)中的值重新初始化搜索窗的大小和位置，再跳转到(2)继续进行。

camshift能有效解决目标变形和遮挡的问题，对系统资源要求不高，时间复杂度低，在简单背景下能够取得良好的跟踪效果。但当背景较为复杂，或者有许多与目标颜色相似像素干扰的情况下，会导致跟踪失败。因为它单纯的考虑颜色直方图，忽略了目标的空间分布特性，所以这种情况下需加入对跟踪目标的预测算法。

Camshift的opencv实现
原文 http://blog.csdn.net/houdy/archive/2004/11/10/175739.aspx

1--Back Projection
计算Back Projection的OpenCV代码。
(1).准备一张只包含被跟踪目标的图片，将色彩空间转化到HSI空间，获得其中的H分量：
IplImage* target=cvLoadImage("target.bmp",-1); //装载图片
IplImage* target_hsv=cvCreateImage( cvGetSize(target), IPL_DEPTH_8U, 3 );
IplImage* target_hue=cvCreateImage( cvGetSize(target), IPL_DEPTH_8U, 3 );
cvCvtColor(target,target_hsv,CV_BGR2HSV);       //转化到HSV空间
cvSplit( target_hsv, target_hue, NULL, NULL, NULL );    //获得H分量

(2).计算H分量的直方图，即1D直方图：
IplImage* h_plane=cvCreateImage( cvGetSize(target_hsv),IPL_DEPTH_8U,1 );
int hist_size[]={255};          //将H分量的值量化到[0,255]
float* ranges[]={ {0,360} };    //H分量的取值范围是[0,360)
CvHistogram* hist=cvCreateHist(1, hist_size, ranges, 1);
cvCalcHist(&target_hue, hist, 0, NULL);
在这里需要考虑H分量的取值范围的问题，H分量的取值范围是[0,360)，这个取值范围的值不能用一个byte来表示，为了能用一个byte表示，需要将H值做适当的量化处理，在这里我们将H分量的范围量化到[0,255]。

(3).计算Back Projection：
IplImage* rawImage;
//get from video frame,unsigned byte,one channel
IplImage* result=cvCreateImage(cvGetSize(rawImage),IPL_DEPTH_8U,1);
cvCalcBackProject(&rawImage,result,hist);
(4). result即为我们需要的.

2--Mean Shift算法
质心可以通过以下公式来计算：
(1).计算区域内0阶矩
for(int i=0;i< height;i++)
for(int j=0;j< width;j++)
M00+=I(i,j)

(2).区域内1阶矩：
for(int i=0;i< height;i++)
for(int j=0;j< width;j++)
{
M10+=i*I(i,j);
M01+=j*I(i,j);
}

(3).则Mass Center为：
Xc=M10/M00; Yc=M01/M00

在OpenCV中，提供Mean Shift算法的函数，函数的原型是：
int cvMeanShift(IplImage* imgprob,CvRect windowIn,
CvTermCriteria criteria,CvConnectedComp* out);
需要的参数为：
(1).IplImage* imgprob：2D概率分布图像，传入；
(2).CvRect windowIn：初始的窗口，传入；
(3).CvTermCriteria criteria：停止迭代的标准，传入；
(4).CvConnectedComp* out:查询结果，传出。
注：构造CvTermCriteria变量需要三个参数，一个是类型，另一个是迭代的最大次数，最后一个表示特定的阈值。例如可以这样构造 criteria：
criteria=cvTermCriteria(CV_TERMCRIT_ITER|CV_TERMCRIT_EPS,10,0.1)。

3--CamShift算法
整个算法的具体步骤分5步：
Step 1：将整个图像设为搜寻区域。
Step 2：初始话Search Window的大小和位置。
Step 3：计算Search Window内的彩色概率分布，此区域的大小比Search Window要稍微大一点。
Step 4：运行MeanShift。获得Search Window新的位置和大小。
Step 5：在下一帧视频图像中，用Step 3获得的值初始化Search Window的位置和大小。跳转到Step 3继续运行。

OpenCV代码：
在OpenCV中，有实现CamShift算法的函数，此函数的原型是：
cvCamShift(IplImage* imgprob, CvRect windowIn,
CvTermCriteria criteria,
CvConnectedComp* out, CvBox2D* box=0);
其中：
imgprob：色彩概率分布图像。
windowIn：Search Window的初始值。
Criteria：用来判断搜寻是否停止的一个标准。
out：保存运算结果,包括新的Search Window的位置和面积。
box：包含被跟踪物体的最小矩形。

更多参考：

带有注释的camshift算法的opencv实现代码见：
http://download.csdn.net/source/1663015

Introduction To Mean Shift Algorithm

http://saravananthirumuruganathan.wordpress.com/2010/04/01/introduction-to-mean-shift-algorithm/

Its been quite some time since I wrote a Data Mining post . Today, I intend to post on Mean Shift – a really cool but not very well known algorithm. The basic idea is quite simple but the results are amazing. It was invented long back in 1975 but was not widely used till two papers applied the algorithm to Computer Vision.

I learned this algorithm in my Advanced Data Mining course and I wrote the lecture notes on it. So here I am trying to convert my lecture notes to a post. I have tried to simplify it – but this post is quite involved than the other posts.

It is quite sad that there exists no good post on such a good algorithm. While writing my lecture notes, I struggled a lot for good resources . The 3 “classic" papers on Mean Shift are quite hard to understand. Most of the other resources are usually from Computer Vision courses where Mean Shift is taught lightly as yet another technique for vision tasks (like segmentation) and contains only the main intuition and the formulas.

As a disclaimer, there might be errors in my exposition – so if you find anything wrong please let me know and I will fix it. You can always check out the reference for more details. I have not included any graphics in it but you can check the ppt given in the references for an animation of Mean Shift.

Introduction

Mean Shift is a powerful and versatile non parametric iterative algorithm that can be used for lot of purposes like finding modes, clustering etc. Mean Shift was introduced in Fukunaga and Hostetler [1] and has been extended to be applicable in other fields like Computer Vision.This document will provide a discussion of Mean Shift , prove its convergence and slightly discuss its important applications.

Intuitive Idea of Mean Shift

This section provides an intuitive idea of Mean shift and the later sections will expand the idea. Mean shift considers feature space as a empirical probability density function. If the input is a set of points then Mean shift considers them as sampled from the underlying probability density function. If dense regions (or clusters) are present in the feature space , then they correspond to the mode (or local maxima) of the probability density function. We can also identify clusters associated with the given mode using Mean Shift.

For each data point, Mean shift associates it with the nearby peak of the dataset’s probability density function. For each data point, Mean shift defines a window around it and computes the mean of the data point . Then it shifts the center of the window to the mean and repeats the algorithm till it converges. After each iteration, we can consider that the window shifts to a more denser region of the dataset.

At the high level, we can specify Mean Shift as follows :
1. Fix a window around each data point.
2. Compute the mean of data within the window.
3. Shift the window to the mean and repeat till convergence.

Preliminaries

Kernels :

A kernel is a function that satisfies the following requirements :

1. $\int_{R^{d}}\phi(x)=1$

2. $\phi(x)\geq0$

Some examples of kernels include :

1. Rectangular $\phi(x)=\begin{cases} 1 & a\leq x\leq b\\ 0 & else\end{cases}$

2. Gaussian $\phi(x)=e^{-\frac{x^{2}}{2\sigma^{2}}}$

3. Epanechnikov $\phi(x)=\begin{cases} \frac{3}{4}(1-x^{2}) & if\;|x|\leq1\\ 0 & else\end{cases}$

Kernel Density Estimation

Kernel density estimation is a non parametric way to estimate the density function of a random variable. This is usually called as the Parzen window technique. Given a kernel K, bandwidth parameter h , Kernel density estimator for a given set of d-dimensional points is

$\hat{f}(x)=\frac{1}{nh^{d}}\sum_{i=1}^{n}K\left(\frac{x-x_{i}}{h}\right)$

Gradient Ascent Nature of Mean Shift

Mean shift can be considered to based on Gradient ascent on the density contour. The generic formula for gradient ascent is ,

$x_{1}=x_{0}+\eta f'(x_{0})$

Applying it to kernel density estimator,

$\hat{f}(x)=\frac{1}{nh^{d}}\sum_{i=1}^{n}K\left(\frac{x-x_{i}}{h}\right)$

$\bigtriangledown{\displaystyle \hat{f}(x)=\frac{1}{nh^{d}}\sum_{i=1}^{n}K'\left(\frac{x-x_{i}}{h}\right)}$

Setting it to 0 we get,

$\sum_{i=1}^{n}K'\left(\frac{x-x_{i}}{h}\right)\overrightarrow{x}=\sum_{i=1}^{n}K'\left(\frac{x-x_{i}}{h}\right)\overrightarrow{x_{i}}$

Finally , we get

$\overrightarrow{x}=\frac{\sum_{i=1}^{n}K'\left(\frac{x-x_{i}}{h}\right)\overrightarrow{x_{i}}}{\sum_{i=1}^{n}K'\left(\frac{x-x_{i}}{h}\right)}$

Mean Shift

As explained above, Mean shift treats the points the feature space as an probability density function . Dense regions in feature space corresponds to local maxima or modes. So for each data point, we perform gradient ascent on the local estimated density until convergence. The stationary points obtained via gradient ascent represent the modes of the density function. All points associated with the same stationary point belong to the same cluster.

Assuming $g(x)=-K'(x)$ , we have

$m(x)=\frac{\sum_{i=1}^{n}g\left(\frac{x-x_{i}}{h}\right)x_{i}}{\sum_{i=1}^{n}g\left(\frac{x-x_{i}}{h}\right)}-x$

The quantity $m(x)$ is called as the mean shift. So mean shift procedure can be summarized as : For each point $x_{i}$

1. Compute mean shift vector $m(x_{i}^{t})$

2. Move the density estimation window by $m(x_{i}^{t})$

3. Repeat till convergence

Using a Gaussian kernel as an example,

1. $y_{i}^{0}=x_{i}$
2. $y_{i}^{t+1}=\frac{\sum_{i=1}^{n}x_{j}e^{\frac{-|y_{i}^{t}-x_{j}|^{2}}{h^{2}}}}{\sum_{i=1}^{n}e^{\frac{-|y_{i}^{t}-x_{j}|^{2}}{h^{2}}}}$

Proof Of Convergence

Using the kernel profile,

$y^{t+1}=\frac{\sum_{i=1}^{n}x_{i}k(||\frac{y^{t}-x_{i}}{h}||^{2})}{\sum_{i=1}^{n}k(||\frac{y^{t}-x_{i}}{h}||^{2})}$

To prove the convergence , we have to prove that $f(y^{t+1})\geq f(y^{t})$

$f(y^{t+1})-f(y^{t})={\displaystyle \sum_{i=1}^{n}}k(||\frac{y^{t+1}-x_{i}}{h}||^{2})-{\displaystyle \sum_{i=1}^{n}}k(||\frac{y^{t}-x_{i}}{h}||^{2})$

But since the kernel is a convex function we have ,

$k(y^{t+1})-k(y^{t})\geq k'(y^{t})(y^{t+1}-y^{t})$

Using it ,

$f(y^{t+1})-f(y^{t})\geq{\displaystyle \sum_{i=1}^{n}}k'(||\frac{y^{t}-x_{i}}{h}||^{2})(||\frac{y^{t+1}-x_{i}}{h}||^{2}-||\frac{y^{t}-x_{i}}{h}||^{2})$

$=\frac{1}{h^{2}}{\displaystyle \sum_{i=1}^{n}}k'(||\frac{y^{t}-x_{i}}{h}||^{2})(y^{(t+1)^{2}}-2y^{t+1}x_{i}+x_{i}^{2}-(y^{t^{2}}-2y^{t}x_{i}+x_{i}^{2}))$

$=\frac{1}{h^{2}}{\displaystyle \sum_{i=1}^{n}}k'(||\frac{y^{t}-x_{i}}{h}||^{2})(y^{(t+1)^{2}}-y^{t^{2}}-2(y^{t+1}-y^{t})^{T}x_{i})$

$=\frac{1}{h^{2}}{\displaystyle \sum_{i=1}^{n}}k'(||\frac{y^{t}-x_{i}}{h}||^{2})(y^{(t+1)^{2}}-y^{t^{2}}-2(y^{t+1}-y^{t})^{T}y^{t+1})$

$=\frac{1}{h^{2}}{\displaystyle \sum_{i=1}^{n}}k'(||\frac{y^{t}-x_{i}}{h}||^{2})(y^{(t+1)^{2}}-y^{t^{2}}-2(y^{(t+1)^{2}}-y^{t}y^{t+1}))$

$=\frac{1}{h^{2}}{\displaystyle \sum_{i=1}^{n}}k'(||\frac{y^{t}-x_{i}}{h}||^{2})(y^{(t+1)^{2}}-y^{t^{2}}-2y^{(t+1)^{2}}+2y^{t}y^{t+1})$

$=\frac{1}{h^{2}}{\displaystyle \sum_{i=1}^{n}}k'(||\frac{y^{t}-x_{i}}{h}||^{2})(-y^{(t+1)^{2}}-y^{t^{2}}+2y^{t}y^{t+1})$

$=\frac{1}{h^{2}}{\displaystyle \sum_{i=1}^{n}}k'(||\frac{y^{t}-x_{i}}{h}||^{2})(-1)(y^{(t+1)^{2}}+y^{t^{2}}-2y^{t}y^{t+1})$

$=\frac{1}{h^{2}}{\displaystyle \sum_{i=1}^{n}-}k'(||\frac{y^{t}-x_{i}}{h}||^{2})(||y^{t+1}-y^{t}||^{2})$

$\geq0$

Thus we have proven that the sequence $\{f(j)\}_{j=1,2...}$ is convergent. The second part of the proof in [2] which tries to prove the sequence $\{y_{j}\}_{j=1,2,...}$ is convergent is wrong.

Improvements to Classic Mean Shift Algorithm

The classic mean shift algorithm is time intensive. The time complexity of it is given by $O(Tn^{2})$ where $T$ is the number of iterations and $n$ is the number of data points in the data set. Many improvements have been made to the mean shift algorithm to make it converge faster.

One of them is the adaptive Mean Shift where you let the bandwidth parameter vary for each data point. Here, the $h$ parameter is calculated using kNN algorithm. If $x_{i,k}$ is the k-nearest neighbor of $x_{i}$ then the bandwidth is calculated as

$h_{i}=||x_{i}-x_{i,k}||$

Here we use $L_{1}$ or $L_{2}$ norm to find the bandwidth.

An alternate way to speed up convergence is to alter the data points
during the course of Mean Shift. Again using a Gaussian kernel as
an example,

1. $y_{i}^{0}=x_{i}$
2. $y_{i}^{t+1}=\frac{\sum_{i=1}^{n}x_{j}e^{\frac{-|y_{i}^{t}-x_{j}|^{2}}{h^{2}}}}{\sum_{i=1}^{n}e^{\frac{-|y_{i}^{t}-x_{j}|^{2}}{h^{2}}}}$
3. $x_{i}=y_{i}^{t+1}$

Other Issues

1. Even though mean shift is a non parametric algorithm , it does require the bandwidth parameter h to be tuned. We can use kNN to find out the bandwidth. The choice of bandwidth in influences convergence rate and the number of clusters.
2. Choice of bandwidth parameter h is critical. A large h might result in incorrect
clustering and might merge distinct clusters. A very small h might result in too many clusters.

3. When using kNN to determining h, the choice of k influences the value of h. For good results, k has to increase when the dimension of the data increases.
4. Mean shift might not work well in higher dimensions. In higher dimensions , the number of local maxima is pretty high and it might converge to a local optima soon.
5. Epanechnikov kernel has a clear cutoff and is optimal in bias-variance tradeoff.

Applications of Mean Shift

Mean shift is a versatile algorithm that has found a lot of practical applications – especially in the computer vision field. In the computer vision, the dimensions are usually low (e.g. the color profile of the image). Hence mean shift is used to perform lot of common tasks in vision.

Clustering

The most important application is using Mean Shift for clustering. The fact that Mean Shift does not make assumptions about the number of clusters or the shape of the cluster makes it ideal for handling clusters of arbitrary shape and number.

Although, Mean Shift is primarily a mode finding algorithm , we can find clusters using it. The stationary points obtained via gradient ascent represent the modes of the density function. All points associated with the same stationary point belong to the same cluster.

An alternate way is to use the concept of Basin of Attraction. Informally, the set of points that converge to the same mode forms the basin of attraction for that mode. All the points in the same basin of attraction are associated with the same cluster. The number of clusters is obtained by the number of modes.

Computer Vision Applications

Mean Shift is used in multiple tasks in Computer Vision like segmentation, tracking, discontinuity preserving smoothing etc. For more details see [2],[8].

Comparison with K-Means

Note : I have discussed K-Means at K-Means Clustering Algorithm. You can use it to brush it up if you want.

K-Means is one of most popular clustering algorithms. It is simple,fast and efficient. We can compare Mean Shift with K-Means on number of parameters.

One of the most important difference is that K-means makes two broad assumptions – the number of clusters is already known and the clusters are shaped spherically (or elliptically). Mean shift , being a non parametric algorithm, does not assume anything about number of clusters. The number of modes give the number of clusters. Also, since it is based on density estimation, it can handle arbitrarily shaped clusters.

K-means is very sensitive to initializations. A wrong initialization can delay convergence or some times even result in wrong clusters. Mean shift is fairly robust to initializations. Typically, mean shift is run for each point or some times points are selected uniformly from the feature space [2] . Similarly, K-means is sensitive to outliers but Mean Shift is not very sensitive.

K-means is fast and has a time complexity $O(knT)$ where k is the number of clusters, n is the number of points and T is the number of iterations. Classic mean shift is computationally expensive with a time complexity $O(Tn^{2})$ .

Mean shift is sensitive to the selection of bandwidth, $h$ . A small $h$ can slow down the convergence. A large $h$ can speed up convergence but might merge two modes. But still, there are many techniques to determine $h$ reasonably well.

Update [30 Apr 2010] : I did not expect this reasonably technical post to become very popular, yet it did ! Some of the people who read it asked for a sample source code. I did write one in Matlab which randomly generates some points according to several gaussian distribution and the clusters using Mean Shift . It implements both the basic algorithm and also the adaptive algorithm. You can download my Mean Shift code here. Comments are as always welcome !

References

1. Fukunaga and Hostetler, "The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition", IEEE Transactions on Information Theory vol 21 , pp 32-40 ,1975
2. Dorin Comaniciu and Peter Meer, Mean Shift : A Robust approach towards feature space analysis, IEEE Transactions on Pattern Analysis and Machine Intelligence vol 24 No 5 May 2002.
3. Yizong Cheng , Mean Shift, Mode Seeking, and Clustering, IEEE Transactions on Pattern Analysis and Machine Intelligence vol 17 No 8 Aug 1995.
4. Mean Shift Clustering by Konstantinos G. Derpanis
5. Chris Ding Lectures CSE 6339 Spring 2010.
6. Dijun Luo’s presentation slides.
7. cs.nyu.edu/~fergus/teaching/vision/12_segmentation.ppt

8. Dorin Comaniciu, Visvanathan Ramesh and Peter Meer, Kernel-Based Object Tracking, IEEE Transactions on Pattern Analysis and Machine Intelligence vol 25 No 5 May 2003.
9. Dorin Comaniciu, Visvanathan Ramesh and Peter Meer, The Variable Bandwidth Mean Shift and Data-Driven Scale Selection, ICCV 2001.