Greedy Algorithm

Greedy algorithm works only if the local optimum is equal to the global optimum.

活动选择问题

Consider any nonempty subproblem $S_k$, and let am be an activity in $S_k$ with the earliest finish time. Then am is included in some maximum-size subset of mutually compatible activities of $S_k$

背包问题

动态规划算法

f[i][v]：表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。

状态转移方程是：f[i][v]=max{f[i-1][v],f[i-1][v-weight[i]]+value[i]}

“将前i件物品放入容量为v的背包中”这个子问题，如果只考虑第i件物品放或者不放，那么就可以转化为只涉及前i-1件物品的问题：

1. 如果不放第i件物品，则问题转化为“前i-1件物品放入容量为v的背包中”；

2. 如果放第i件物品，则问题转化为“前i-1件物品放入剩下的容量为v-weight[i]的背包中”，此时能获得的最大价值就是f [i-1][v-weight[i]]，再加上通过放入第i件物品获得的价值value[i]。

f[i][v]的值就是1、2中最大的那个值。

// 背包问题    
#include      
#include   
using namespace std;  
  
#define N 3 // N件宝贝    
#define C 5 // C是背包的总capacity    
  
int main()  
{  
    int value[N + 1] = { 0, 60, 100, 120 }; // 价值    
    int weight[N + 1] = { 0, 1, 2, 3 };     // 重量    
    int f[N + 1][C + 1] = { 0 };   // f[i][j]表示在背包容量为j的情况下，前i件宝贝的最大价值    
  
    int i = 1;  
    int j = 1;  
    for (i = 1; i <= N; i++)        //外循环控制物品数量，确保每个物品都会被遍历到  
    {  
        /*for (j = weight[i]; j <= C; j++)      //内循环控制物品的重量，确保能够遍历出“以前每个物品放入时的最大价值f[i][j]” 
        { 
            int x = f[i - 1][j];        //不放第i件物品 
            int y = f[i - 1][j - weight[i]] + value[i];      //放入第i件物品 
            f[i][j] = max(x, y); 
        }*/  
  
        for (j = 1; j <= C; j++)  
        {  
            // 递推关系式    
            if (j < weight[i])  
            {  
                f[i][j] = f[i - 1][j];  
            }  
            else  
            {  
                int x = f[i - 1][j];  
                int y = f[i - 1][j - weight[i]] + value[i];  
                f[i][j] = max(x, y);  
            }  
        }  
    }  
  
    for (i = 0; i <= N; i++)  
    {  
        for (j = 0; j <= C; j++)  
        {  
            printf("%4d ", f[i][j]);  
        }  
  
        cout << endl;  
    }  
  
    cout << endl << "选取的最大价值是：" << f[N][C] << endl;  
    cout << "选取的物品如下：" << endl;  
    i = N, j = C;  
    while (i)  
    {  
        if (f[i][j] == (f[i - 1][j - weight[i]] + value[i]))  
        {  
            cout << i << ":" << "weight=" << weight[i] << ", value=" << value[i] << endl;  
            j -= weight[i];  
        }  
        i--;  
    }  
  
    cout << endl;  
    return 0;  
}  

优化空间复杂度：

上面f[i][v]使用二维数组存储的，可以优化为一维数组f[v]，将主循环改为：

for i = 1…N；

for v = V…0；

f[v] = max（f[v]， f[v-c[i]]+w[i]）；

即将第二层循环改为从V…0，逆序。

#include   
#include   
using namespace std;  
  
const int MIN = 0x80000000;  
const int N = 3;   //物品数量  
const int V = 5;  //背包容量  
int f[V + 1];              // 一维数组  
  
int Package(int *W, int *C, int N, int V)  
{  
    int i, j;  
    memset(f, 0, sizeof(f));  //初始化为0  
  
    for (i = 1; i <= V; i++)       //此步骤是解决是否恰好满足背包容量，  
        f[i] = MIN;                // 若“恰好”满足背包容量，即正好装满背包，则加上此步骤; 若不需要“恰好”，则初始化为0  
  
    for (i = 1; i <= N; i++)  
        for (j = V; j >= C[i]; j--)    //注意此处与解法一是顺序不同的，弄清原因  
        {  
            f[j] = (f[j]>f[j - C[i]] + W[i]) ? f[j] : (f[j - C[i]] + W[i]);  
            cout << "f[" << i << "][" << j << "]=" << f[j] << endl;  
        }  
  
    return f[V];  
}  
  
void main()  
{  
    int W[4] = { 0, 7, 5, 8 };      //物品权重  
    int C[4] = { 0, 2, 3, 4 };      //物品大小  
  
    int result = Package(W, C, N, V);  
  
    if (result > 0)  
    {  
        cout << endl;  
        cout << "the opt value:" << result << endl;  
    }  
    else  
        cout << "can not find the opt value" << endl;    // 可能不存在正好装满背包的解  
}  

在求最优解的背包问题中，一般有两种不同的问法：

1.要求“恰好装满背包”时的最优解：
在初始化时除了 f[0] 为 0其它f[1…V]均设为 -∞，这样就可以保证最终得到的f[N]是一种恰好装满背包的最优解。如果不能恰好满足背包容量，即不能得到 f[V] 的最优值，则此时 f[V] =-∞，这样就能表示没有找到恰好满足背包容量的最优值。

2.求小于等于背包容量的最优解，即不一定恰好装满背包：
如果并没有要求必须把背包装满，而是只希望价值尽量大，初始化时应该将f[0…V]全部设为0。

Exercise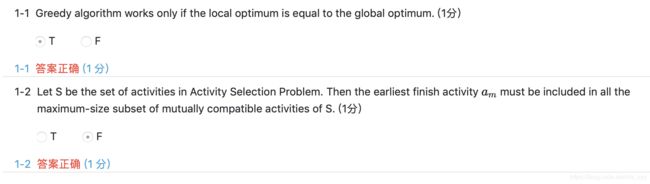

https://blog.csdn.net/zwpf1994/article/details/79083972