c++学习笔记——stack和queue
学习完容器,来看看容器适配器。容器适配器也是STL的组成部分。
目录
deque
概念
迭代器
特点
总结
容器适配器
stack
概念
接口
应用
实现
queue
概念
接口
应用
实现
priority_queue
概念
接口
运用
细节
deque
-
概念
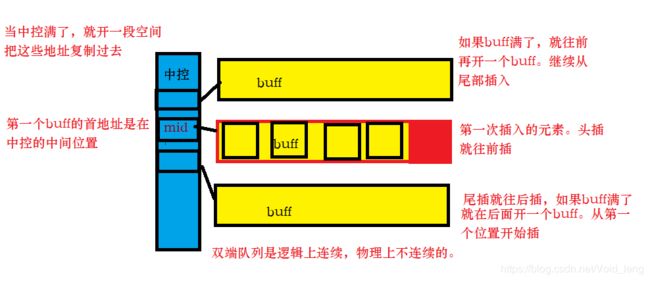
在说容器适配器之前,先来说下双端队列,双端队列也是一个容器。名字是双端队列,但本质可以理解为一个二维数组。双端队列由中控和buff组成。
-
迭代器
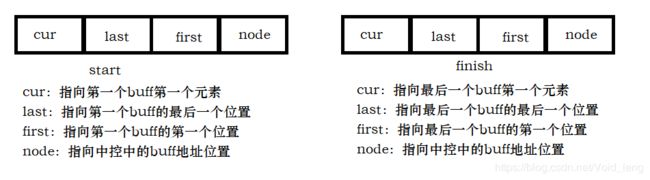
双端队列底层是一段假象的连续空间,实际是分段连续的,为了维护其“整体连续”的假象,落在了deque的 迭代器身上。deque的迭代器是两个迭代器,一个start迭代器,一个finish迭代器。类似于begin和end。
-
特点
它综合了list和vector,其特点如下
- 支持随机访问
- 插入和删除的时间复杂度是O(1)
- 开辟空间代价小,不会造成空间碎片
-
总结
deque这个容器不常用,因为虽然综合了vector和list,但是deque赶不上vector和list优势:比如它没有vector的访问效率高。它的接口非常多,毕竟是前两者的综合,由于不常用,所以这里了解原理就好。
容器适配器
容器适配器是一种设计模式,该模式是将一个类的接口转换成用户希望的另外一个接口。例如:
stack(栈)、queue(队列)、priority_queue(优先级队列)都是容器适配器。因为它们在底层只是对其他容器进行了封装,就行接口转换器一样,只是将其他接口转换了一下,而我们虽然用的是适配器,其实底层还是容器。下面来深入理解。
stack
-
概念
在数据结构阶段,就接触到了栈(点击进入)。这里是容器适配器,但是特性不变。栈是先进后出的。而且删除插入等操作都只能在栈顶操作,
-
接口
在c++里,有以下常用接口。
| 函数说明 | 接口说明 |
| stack(const container_type& ctnr = container_type()) | 构造空的栈 |
| bool empty() const | 检测stack是否为空 |
| size_type size() const | 返回stack中元素的个数 |
| value_type& top() | 返回栈顶元素的引用 |
| const value_type& top() const | 返回栈顶元素的const引用 |
| void push (const value_type& val) | 将元素val压入stack中 |
| void pop() | 将stack中尾部的元素弹出 |
-
应用
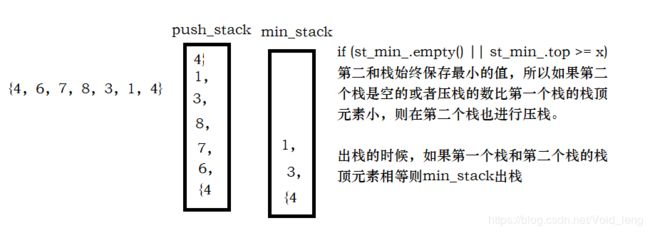
- 设计一个支持 push,pop,top 操作,并能在常数时间内检索到最小元素的栈。
- push(x) -- 将元素 x 推入栈中。
- pop() -- 删除栈顶的元素。
- top() -- 获取栈顶元素。
- getMin() -- 检索栈中的最小元素。
class MinStack {
public:
MinStack()
{}
void push(int x)
{
if (st_min_.empty() || st_min_.top >= x)
{
st_min_.push(x);
}
st_push_.push(x);
}
void pop()
{
if (st_push_.top() == st_min_.top())
{
st_min_.pop();
}
st_push_.pop();
}
int top()
{
return st_push_.top();
}
int getMin()
{
return st_min_.top();
}
private:
stack st_push_;
stack st_min_;
}; -
栈的弹出压入序列
- 输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1, 2, 3, 4, 5是某栈的压入顺序,序列4, 5, 3, 2, 1是该压栈序列对应的一个弹出序列,但4, 3, 5, 1, 2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
class Solution2 {
public:
bool IsPopOrder(vector pushV, vector popV) {
if (pushV.size() != popV.size())
{
return false;
}
//记录pushV的下标
int index = 0;
//记录popV的下标
int outdex = 0;
//创建一个栈来进行入栈出栈
stack test;
int in_size = pushV.size();
int out_size = popV.size();
//如果popV走完了,就说明只是一个出栈顺序。
while (outdex < out_size)
{
//如果栈还是空的我们就先入栈
//或者栈顶元素不等于我们的popV,就进行入栈
while (test.empty() || test.top() != popV[outdex])
{
//如果pushV走完了,test不是空栈,说明这不是一个出栈顺序
if (index < in_size)
{
test.push(pushV[index++]);
}
else
{
return false;
}
}
++outdex;
test.pop();
}
return true;
}
}; - 使用栈实现队列的下列操作
- push(x) -- 将一个元素放入队列的尾部。
- pop() -- 从队列首部移除元素。
- peek() -- 返回队列首部的元素。
- empty() -- 返回队列是否为空。
class Myqueen {
public:
Myqueen()
{}
void push(int x)
{
st_tail_.push(x);
}
int pop()
{
if (!st_front_.empty())
{
int tmp = st_front_.top();
st_front_.pop();
return tmp;
}
else
{
while (!st_tail_.empty())
{
st_front_.push(st_tail_.top());
st_tail_.pop();
}
if (st_front_.empty())
{
return false;
}
else
{
int tmp = st_front_.top();
st_front_.pop();
return tmp;
}
}
}
int top()
{
if (!st_front_.empty())
{
return st_front_.top();
}
else
{
while (!st_tail_.empty())
{
st_front_.push(st_tail_.top());
st_tail_.pop();
}
if (st_front_.empty())
{
return false;
}
else
{
return st_front_.top();
}
}
}
private:
stack st_tail_;
stack st_front_;
}; -
实现
现在来说一说stack是怎么实现的,因为stack是一种适配器,所以底层只要用其他容器的接口就行。stack只能在栈顶操作,所以只要支持下面操作接口的容器就能实现一个栈
- push_back():尾插
- pop_back():尾删
- back():获取尾部元素
- empty():判断是否为空
那么有哪些容器呢?就是下面的这些容器,因为它们都支持上述的接口
- deque(默认的,栈是不需要随机访问的,它的扩容的代价小,不会造成内存碎片)
- vector
- list
template>
class Stack
{
public:
void Push(const T& val)
{
con_.push_back();
}
void Pop()
{
con_.pop();
}
bool Empty()
{
return con_.empty();
}
T& top()
{
return con_.back();
}
private:
containser con_;
}; queue
-
概念
数据结构阶段,也接触过。(队列点击进入)队列是一种容器适配器,专门用于在FIFO上下文(先进先出)中操作,其中从容器一端插入元素,另一端提取元素。
-
接口
| 接口声明 | 接口说明 |
| queue (const container_type& ctnr = container_type()) | 构造空的队列 |
| bool empty() const | 检测队列是否为空,是返回true,否则 返回false |
| size_type size() const | 返回队列中有效元素的个数 |
| value_type& front() | 返回队头元素的引用 |
| const value_type& front() const | 返回队头元素的const引用 |
| value_type& back() | 返回队尾元素的引用 |
| const value_type& back() const | 返回队尾元素的cosnt引用 |
| void push(value_type& val) | 在队尾将元素val入队列 |
| void pop() | 将队头元素出队列 |
-
应用
- 给定一个二叉树,返回其按层次遍历的节点值。 (即逐层地,从左到右访问所有节点)。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
int treehigh(TreeNode* root)
{
if (!root)
{
return 0;
}
int left_ = treehigh(root->left);
int right_ = treehigh(root->right);
return left_ > right_ ? left_ + 1 : right_ + 1;
}
vector> levelOrder(TreeNode* root) {
int height = treehigh(root);
vector> treeVec;
treeVec.resize(height);
queue Pnode;
queue Index;
TreeNode* tmp = root;
if (!tmp)
{
return treeVec;
}
Pnode.push(tmp);
Index.push(0);
while (!Pnode.empty())
{
tmp = Pnode.front();
Pnode.pop();
int index = Index.front();
Index.pop();
treeVec[index].push_back(tmp->val);
if (tmp->left)
{
Pnode.push(tmp->left);
Index.push(index + 1);
}
if (tmp->right)
{
Pnode.push(tmp->right);
Index.push(index + 1);
}
}
return treeVec;
}
}; -
实现
queue同stack一样,都是适配器,所以只要有容器满足下面的接口,同样实现方式。
- empty():检测队列是否为空
- size():返回队列中有效元素的个数
- front():返回队头元素的引用
- back():返回队尾元素的引用
- push_back():在队列尾部入队列
- pop_front():在队列头部出队列
但是它不能用vector。因为vector实现头插效率太低,而且也没有push_front、pop_front()等操作
- deque(默认的,队列是不需要随机访问的,它的扩容的代价小,不会造成内存碎片)
- list
template>
class Queue
{
public:
void Push(const T& val)
{
con_.push_back(val);
}
void Pop()
{
con_.pop_front();
}
T& Front()
{
return con_.front();
}
T& Back()
{
return con_.back();
}
bool Emtpy()
{
return con_.empty();
}
private:
containser con_;
};
priority_queue
-
概念
优先队列是一种容器适配器,它在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。 默认情况下priority_queue是大堆。在前面数据结构中学到过堆(点击进入-复习)。
-
接口
| 接口声明 |
接口说明 |
| priority_queue(const Compare& x = Compare(), const Container& y = Container() ); | 构造一个空的优先 级队列 |
| priority_queue(InputIterator first, InputIterator last, const Compare& comp = Compare(), const Container& ctnr = Container()); | 用[first, last)区间 中的元素构造优先级队列 |
| bool empty( ) const | 检测优先级队列是 否为空, |
| const value_type& top ( ) const | 返回优先级队列中 最大(最小元素), 即堆顶元素 |
| void push ( const T& x ) | 在优先级队列中插 入元素x |
| void pop ( ) | 删除优先级队列中 最大(最小)元素即堆顶元素 |
-
运用
- 在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
class Solution {
public:
int findKthLargest(vector& nums, int k)
{ // 将数组中的元素先放入优先级队列中
priority_queue p(nums.begin(), nums.end());
// 将优先级队列中前k-1个元素删除掉
for(int i= 0; i < k-1; ++i)
{
p.pop();
}
return p.top();
}
};
-
细节
- 优先级队列是堆,而且默认是大堆
- 如果在priority_queue中放自定义类型的数据,用户需要在自定义类型中提供> 或者< 的重载。
- 有些情况下,用户可能需要提供比较器规则