Algorithms - Data Structure - Querying a Binary Search Tree - 二叉搜索树的查询

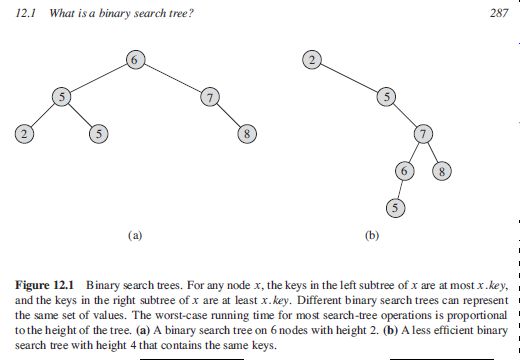
概念
    binary search tree 二叉搜索树的性质: 设 x 是 binary search tree中的一个节点。
    如果y是x左子树中的一个节点, 那么y.key<=x.key
    如果y是x右子树中的一个节点, 那么y.key>=x.key
    
    BST 数据结构参考： https://www.cnblogs.com/zzyzz/p/13000550.html
　　

     

 

Python Programming

    BST 支持 search, minimum, maximum, successor, predecessor 相关查询操作.
    
    Search 查询:
        1. Search 查询的递归版本
　　　　　2. Search 查询的 while 循环版本　　　　　　

# 递归版本
def tree_search(k, x, T):      # x : sub-tree ,  k : the target key.
    keys = [2,4,5,6,7,8]
    if k not in keys:
        return 'NIL'
    ind = keys.index(x.root)
    obj = T[ind]
    if obj.key == k:
        return obj
    else:
        if k < obj.key:
            return tree_search(k, obj.left,T)
        else:
            return tree_search(k, obj.right,T)

# while 版本
def iterative_tree_search( k, x, T):     # x : sub-tree ,  k : the target key.
    keys = [2, 4, 5, 6, 7, 8]
    if k not in keys:
        return 'NIL'
    ind = keys.index(x.root)
    obj = T[ind]
    while  k != obj.key:
        if k < obj.key:
            obj = obj.left
        else:
            obj = obj.right
    return obj

if __name__ == '__main__':
    keys = [2,4,5,6,7,8]
    parent = [4,6,4,'NIL',6,7]
    left = ['NIL',2,'NIL',4,'NIL', 'NIL']
    right = ['NIL',5,'NIL',7,8,'NIL']
    root = 6

    
    #BST 数据结构： https://www.cnblogs.com/zzyzz/p/13000550.html
    T = binary_search_tree(keys,parent,left,right,root)

    for j in [2,4,5,6,7,8,10]:
        x = tree_search(j,T,T)
        if isinstance(x, tree_element):
            print('recursive search : ',x.key, x)
        else:
            print('recursive search : ', x, 'Not Found: ' + str(j))

    for k in [2, 4, 5, 6, 7, 8, 10]:
        y = iterative_tree_search(k,T,T)
        if isinstance(y, tree_element):
            print('While search : ', y.key, y)
        else:
            print('While search : ', y, 'Not Found: ' + str(k))

结果打印:
recursive search :  2 <__main__.tree_element object at 0x00000000029DDCC0>
recursive search :  4 <__main__.tree_element object at 0x00000000029DDDD8>
recursive search :  5 <__main__.tree_element object at 0x00000000029DDCF8>
recursive search :  6 <__main__.tree_element object at 0x00000000029DDFD0>
recursive search :  7 <__main__.tree_element object at 0x00000000029DDD68>
recursive search :  8 <__main__.tree_element object at 0x00000000029DDE10>
recursive search :  NIL Not Found: 10
While search :  2 <__main__.tree_element object at 0x00000000029DDE48>
While search :  4 <__main__.tree_element object at 0x00000000029DDE80>
While search :  5 <__main__.tree_element object at 0x00000000029DDEB8>
While search :  6 <__main__.tree_element object at 0x00000000029DDFD0>
While search :  7 <__main__.tree_element object at 0x00000000029DDF98>
While search :  8 <__main__.tree_element object at 0x00000000029DDF60>
While search :  NIL Not Found: 10

    Minimum / Maximum:

def tree_minimum(x, T):
    x = T[T.keys.index(x.root)]
    while x.left != 'NIL':
        x = x.left
    return x

def tree_maximum(x, T):
    x = T[T.keys.index(x.root)]
    while x.right != 'NIL':
        x = x.right
    return x


if __name__ == '__main__':
    keys = [2,4,5,6,7,8]
    parent = [4,6,4,'NIL',6,7]
    left = ['NIL',2,'NIL',4,'NIL', 'NIL']
    right = ['NIL',5,'NIL',7,8,'NIL']
    root = 6

    T = binary_search_tree(keys,parent,left,right,root)
　　
    for i in T.keys:
　　　　 print('The sub-tree with a root of : ', i)
　　　　 inorder_tree_walk(T, i, 'N')
        print('=' * 33)

for obj in T:
        print('The sub-tree with a root of : ', obj.root)
        print('min', tree_minimum(obj,T).key, tree_minimum(obj,T))
        print('max', tree_maximum(obj,T).key, tree_minimum(obj,T))
        print('=' * 33)


结果打印:

#子 BST 的结构 
The sub-tree with a root of :  2
=================================
The sub-tree with a root of :  4
Left Child :  2
Right Child :  5
=================================
The sub-tree with a root of :  5
=================================
The sub-tree with a root of :  6
Left Child :  2
Left Child :  4
Right Child :  5
Right Child :  7
Right Child :  8
=================================
The sub-tree with a root of :  7
Right Child :  8
=================================
The sub-tree with a root of :  8
=================================

# minimum / maximum
The sub-tree with a root of :  2
min 2 <__main__.tree_element object at 0x00000000029B1CC0>
max 2 <__main__.tree_element object at 0x00000000029B1CC0>
=================================
The sub-tree with a root of :  4
min 2 <__main__.tree_element object at 0x00000000029B1C88>
max 5 <__main__.tree_element object at 0x00000000029B1C88>
=================================
The sub-tree with a root of :  5
min 5 <__main__.tree_element object at 0x00000000029B1CF8>
max 5 <__main__.tree_element object at 0x00000000029B1CF8>
=================================
The sub-tree with a root of :  6
min 2 <__main__.tree_element object at 0x00000000029B1E48>
max 8 <__main__.tree_element object at 0x00000000029B1E48>
=================================
The sub-tree with a root of :  7
min 7 <__main__.tree_element object at 0x00000000029B1D68>
max 8 <__main__.tree_element object at 0x00000000029B1D68>
=================================
The sub-tree with a root of :  8
min 8 <__main__.tree_element object at 0x00000000029B1E10>
max 8 <__main__.tree_element object at 0x00000000029B1E10>
=================================

    
    Successor / predecessor:
　　 概念;
    　　给定一个 BST 中的一个结点 x,  
        则结点 x 的 successor 是 大于 x.key 的结点中 key 属性值最小的结点, 如果 x 是该 BST 中最大的结点则返回  NIL;
　　　　 结点 x 的 predecessor 是 小于 x.key 的结点中 key 属性值最大的结点, 如果 x 是该 BST 中最小的结点则返回 NIL. 
　　

def tree_successor(x,T):

    if x.right != 'NIL':
        return tree_minimum(x.right,T)

    y = T[T.keys.index(x.p)]

    if y.right == 'NIL':
        return y
    while y != 'NIL' and x.key == y.right.key:
        x = y
        if y.p == 'NIL':
            return y.p
        y = T[T.keys.index(y.p)]
        
    return y

if __name__ == '__main__':
    keys = [2,4,5,6,7,8]
    parent = [4,6,4,'NIL',6,7]
    left = ['NIL',2,'NIL',4,'NIL', 'NIL']
    right = ['NIL',5,'NIL',7,8,'NIL']
    root = 6

    T = binary_search_tree(keys,parent,left,right,root)

    # 子 BST
    for i in T.keys:
        print('The sub-tree with a root of : ', i)
        inorder_tree_walk(T, i, 'N')
        print('=' * 33)

    for obj4 in T:
        print('The sub-tree with a root of : ', obj4.root)
        s = tree_successor(obj4, T)
        if isinstance(s, str):
            print('successor ->' + str(obj4.key), s)
        else:
            print('successor ->' + str(obj4.key), s.key, s, obj4.p)
        print('=' * 33)


结果打印

# 子 BST 
The sub-tree with a root of :  2
=================================
The sub-tree with a root of :  4
Left Child :  2
Right Child :  5
=================================
The sub-tree with a root of :  5
=================================
The sub-tree with a root of :  6
Left Child :  2
Left Child :  4
Right Child :  5
Right Child :  7
Right Child :  8
=================================
The sub-tree with a root of :  7
Right Child :  8
=================================
The sub-tree with a root of :  8
=================================


# 每一个子 BST 的 successor
=================================
The sub-tree with a root of :  2
successor ->2 4 <__main__.tree_element object at 0x00000000029C7DD8> 4
=================================
The sub-tree with a root of :  4
successor ->4 5 <__main__.tree_element object at 0x00000000029C7CF8> 6
=================================
The sub-tree with a root of :  5
successor ->5 6 <__main__.tree_element object at 0x00000000029C7FD0> 4
=================================
The sub-tree with a root of :  6
successor ->6 7 <__main__.tree_element object at 0x00000000029C7D68> NIL
=================================
The sub-tree with a root of :  7
successor ->7 8 <__main__.tree_element object at 0x00000000029C7E10> 6
=================================
The sub-tree with a root of :  8
successor ->8 NIL
=================================

 

 Reference,

       1. Introduction to Algorithms