《程序设计与算法》之【贪心算法】

• 圣诞老人的礼物（百练4110）
• 电影节（百练4151）
• Stall Reservations（百练3190）
• Radar Installation（百练1328）

圣诞老人的礼物（百练4110）

题目描述
圣诞节来临了，圣诞老人准备分发糖果，现 在有多箱不同的糖果，每箱糖果有自己的价值和重 量，每箱糖果都可以拆分成任意散装组合带走。圣 诞老人的驯鹿雪橇最多只能装下重量W的糖果，请 问圣诞老人最多能带走多大价值的糖果。

输入：
第一行由两个部分组成，分别为糖果箱数正整数n(1 <= n <= 100)，驯鹿能承受的最大重量正整数w（0 < w < 10000），两个数用空格隔开。其余n行每行对应一箱糖 果，由两部分组成，分别为一箱糖果的价值正整数v和重 量正整数w，中间用空格隔开。

输出：
输出圣诞老人能带走的糖果的最大总价值，保留1位小数 。输出为一行，以换行符结束。

样例输入：
4 15
100 4
412 8
266 7
591 2

样例输出：
1193.0

解题思路
按礼物的价值/重量比从大到小依次选取礼物，对选 取的礼物尽可能多地装，直到达到总重量w，复杂度： O(nlogn)

解答

#include 
using namespace std;
const double eps = 1e-6;
struct Candy {
    int v;
    int w;
    bool operator < (const Candy & c) const {
        return double(v)/w - double(c.v)/c.w > eps;
    }
} candies[110];

int main() {
    int n, w;
    scanf("%d%d", &n, &w);
    for (int i = 0; i < n; i++) {
        scanf("%d%d", &candies[i].v, &candies[i].w);
    }
    sort(candies, candies+n, cmp);
    int totalW = 0;
    double totalV = 0;
    for (int i = 0; i < n; i++) {
        if (totalW + candies[i].w <= w) {
            totalW += candies[i].w;
            totalV += candies[i].v;
        } else {
            totalV += candies[i].v * double(w-totalW)/candies[i].w;
            break;
        }
    }
    printf("%.1f\n", totalV);
    return 0;
}

每一步行动总是按某种指标选取最优的操作来进行，
该指标只看眼前，并不考虑以后可能造成的影响。“圣诞老人礼物”题，若糖果只能整箱拿，则贪心法错误。

电影节（百练4151）

题目描述
大学生电影节在北大举办! 这天，在北大各地放了多部电影 ，给定每部电影的放映时间区间，区间重叠的电影不可能同时 看（端点可以重合），问李雷最多可以看多少部电影。
输入：
多组数据。每组数据开头是n(n<=100)，表示共n场电影。接下来n行，每行两个整数(均小于1000），表示一场电影的放映区间，n=0则数据结束

输出：
对每组数据输出最多能看几部电影。

Sample Input：
12
1 3
3 4
0 7
3 8
15 19
15 20
10 15
8 18
6 12
5 10
4 14
2 9
0

Sample Output：
5

解题思路
将所有电影按结束时间从小到大排序，第一步选结束时间最早的那部电影。 然后，每步都选和上一部选中的电影不冲突且结束时间最早的电影。
复杂度： O(nlogn)

#include 
using namespace std;
struct Film {
    int b;
    int e;
    bool operatoc < (const Film & f) const {
    return e < f.e;
}
} films[110];

int main() {
    int n;
    while (scanf("%d", &n) && n != 0) {
        for (int i = 0; i < n; i++) {
            scanf("%d%d", &films[i].b, &films[i].e);
        }
        sort(films, films+n, cmp);
        int total = 1;
        int last = 0;
        for (int i = 1; i < n; i++) {
            if (films[i].b >= films[last].e) {
                last = i;
                total++;
            }
        }
        printf("%d\n", total);

    }
    return 0;
}

Stall Reservations（百练3190）

题目描述
有 n头牛（1<=n<=50,000)要挤奶。给定每头牛挤奶的时间区间[A,B] (1<=A<=B<=1,000,000，A,B为整数)。
牛需要呆畜栏里才能挤奶。一个畜栏同一时间只能容纳一头牛。 问至少需要多少个畜栏，才能完成全部挤奶工作，以及每头牛都放哪个畜栏里（Special judged)
去同一个畜栏的两头牛，它们挤奶时间区间哪怕只在端点重合也 是不可以的。

解题思路
贪心解法：
所有奶牛都必须挤奶。到了一个奶牛的挤奶开始时间，就必须为这个奶牛找畜栏。因此按照奶牛的开始时间逐个处理它们，是必然的。
S(x)表示奶牛x的开始时间。E(x)表示x的结束时间。对E(x), x可以是奶牛 ，也可以是畜栏。畜栏的结束时间，就是正在其里面挤奶的奶牛的结束时间。同一个畜栏的结束时间是不断在变的。
1) 把所有奶牛按开始时间从小到大排序。
2) 为第一头奶牛分配一个畜栏。
3) 依次处理后面每头奶牛i。处理 i 时，考虑已分配畜栏中，结束时间最早的畜栏x。
若 E(x) < S(i), 则不用分配新畜栏，i可进入x,并修改E(x)为E(i)
若 E(x) >= S(i)，则分配新畜栏y,记 E(y) = E(i)
直到所有奶牛处理结束

需要用优先队列存放已经分配的畜栏，并使得结束时间最早的畜栏始终 位于队列头部。
复杂度： O(nlogn)

解答

#include 
#include 
#include 
#include 
using namespace std;
struct Cow {
    int b, e; // 挤奶区间起点和终点
    int No;   // 编号
    bool operator < (const Cow & c) const {
        return b < c.b;
    }
} cows[50100];

int pos[50100];   // pos[i]表示编号为i的奶牛去的畜栏编号
struct Stall {
    int end;   // 结束时间
    int No;    // 编号
    bool operator < (const Stall & s) const {
        return end > s.end;
    }
    Stall (int e, int n) : end(e), No(n) {}
};
int main() {
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d%d", &cows[i].b, &cows[i].e);
        cows[i].No = i;
    }
    sort(cows, cows+n);
    int total = 0;
    priority_queue pq;
    for (int i = 0; i < n; i++) {
        if (pq.empty()) {
            ++total;
            pq.push(Stall(cows[i].e, total));
            pos[cows[i].No] = total;
        } else {
            Stall st = pq.top();
            if (st.end < cows[i].b) {   // 端点也不能重合
                pq.pop();
                pos[cows[i].No] = st.No;
                pq.push(Stall(cows[i].e, st.No));
            } else {
                ++total;
                pq.push(Stall(cows[i].e, total));
                pos[cows[i].No] = total;
            }
        }
    }
    printf("%d\n", total);
    for (int i = 0; i < n; i++) {
        printf("%d\n", pos[i]);
    }
    return 0;
}

Radar Installation（百练1328）

题目描述
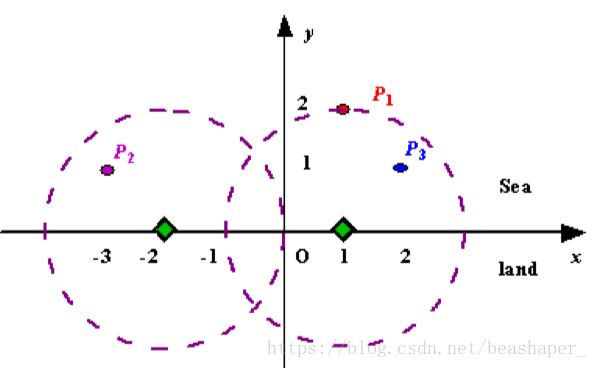
x轴是海岸线，x轴上方是海洋。海洋中有n （1<=n<=1000)个岛屿，可以看作点。
给定每个岛屿的坐标（x,y)，x,y 都是整数。当一个雷达（可以看作点）到岛屿的距离 不超过d(整数），则认为该雷达覆盖了该岛屿。雷达只能放在x轴上。问至少需要多少个雷达才可以覆盖全部岛屿。

输入：
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros

输出：
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. “-1” installation means no solution for that case.

样例输入：
3 2
1 2
-3 1
2 1

1 2
0 2

0 0

样例输出：
Case 1: 2
Case 2: 1

解答思路
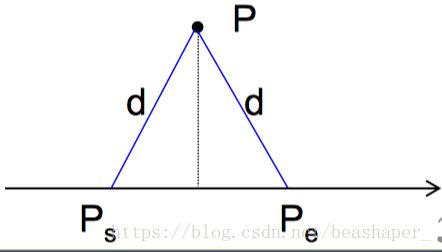
对每个岛屿P,可以算出，覆盖它的雷达，必须位于x轴上的区间[Ps ,Pe ]。
如果有雷达位于某个x轴区间 [a,b]，称该雷达覆盖此区间。问题转换为，至少要在x轴上放几个雷达（点），才能覆盖全部区间[P1s ,P1e ],[P2s ,P2e ]….[Pns ,Pne ]

如果可以找到一个雷达同时覆盖多个区间，那么把这多个区间按起点坐标从小到大排序 ，则最后一个区间(起点最靠右的)k的起点，就能覆盖所有区间。

证明：如果它不能覆盖某个区间x,那么它必然位于 1） x起点的左边 ，或者2）x终点的右边。
情况1) 和 k 的起点是最靠右的矛盾
情况2) 如果发生，则不可能找到一个点同时覆盖x和k，也和前提矛盾
有了这个结论，就可以只挑区间的起点来放置雷达了。

贪心算法：
1 ) 将所有区间按照起点从小到大排序，并编号0 - (n-1)
2 ) 依次考察每个区间的起点，看要不要在那里放雷达。开始，所有区间都没被覆盖，所以目前编号最小的未被覆盖的区间的编号 firstNoConverd = 0

3 ) 考察一个区间 i 的起点 xi 的时候，要看从 firstNoCovered 到区间i1 中是否存在某个区间 c , 没有被 xi 覆盖。如果没有，则先不急于在xi 放雷达，接着往下看。如果有，那么 c 的终点肯定在xi 的左边，因此不可能用同一个雷达覆盖 c 和i。即能覆盖c的点，已经不可能覆盖i和i后面的区间了。此时，为了覆盖c，必须放一个雷达了，放在区间 i-1 的起点即 可覆盖所有从firstNoCovered到 i-1的区间。因为当初考察 i-1的起点 z 时候，并没有发现 z 漏覆盖了从 firstNoCovered 到 i-2 之间的任何一 个区间。
4) 放完雷达后，将 firstNoCovered改为i，再做下去。
复杂度 : O(n^2 )

#include 
#include 
#include 
using namespace std;
struct Island {
    int x1, x2;
    Island(int l, int r): x1(l), x2(r) {}
    bool operator < (const Island& i) const {
        return x1 > i.x1;
    }
};
int main() {
    int n, d;
    int t = 0, ans;
    while (scanf("%d%d", &n, &d) && (n || d)) {
        t++;
        bool flag = true;
        ans = 1;
        priority_queue pq;
        for (int i = 0; i < n; i++) {
            int x, y;
            scanf("%d%d", &x, &y);
            if (abs(y) > d)
                flag = false;
            else
                pq.push(Island(x-sqrt(d*d-y*y), x+sqrt(d*d-y*y)));
        }
        if (flag == false)
            ans = -1;
        else {
            Island p = pq.top();
            pq.pop();
            while (!pq.empty()) {
                Island tmp = pq.top();
                pq.pop();
                if (tmp.x1 > p.x2) {
                    ans++;
                    p = tmp;
                } else if (tmp.x2 < p.x2) {
                    p = tmp;
                }
            }
        }
        printf("Case %d: %d\n", t, ans);
    }
}