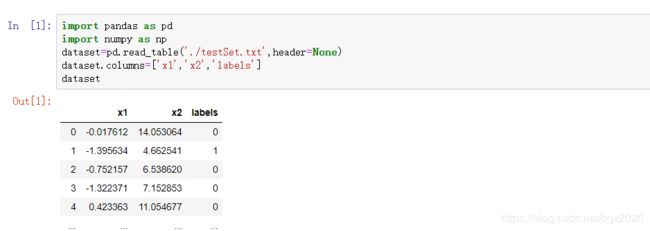
Python算法总结（八）逻辑回归（附手写python实现代码）

通过手写python，加深了对算法原理及流程的理解。

一、算法类型

有监督的分类算法

二、算法原理

损失函数

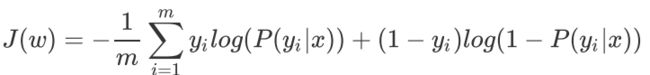
带L1正则化的损失函数

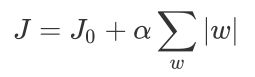
下带L2正则化的损失函数

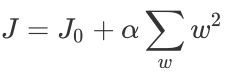
以下对不带正则化的损失函数求解w：
批量梯度下降法BGD求解w的公式

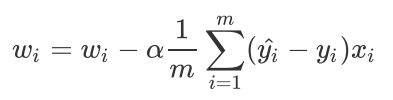
随机梯度下降法SGD求解w的公式

小批量梯度下降法MBGD求解w的公式

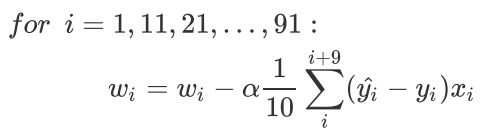
三、手写Python算法

注：不带正则化

# 辅助函数1：定义sigmoid函数
def sigmoid(x):
    s=1 / (1+ np.exp(-x))
    return s

# 辅助函数2：定义标准化函数

def normalizer(xmat):
    #xmat：特征矩阵
    inmat=xmat.copy()
    means=np.mean(inmat,axis=0)
    std=np.std(inmat,axis=0)
    result=(inmat-means)/std
    return result

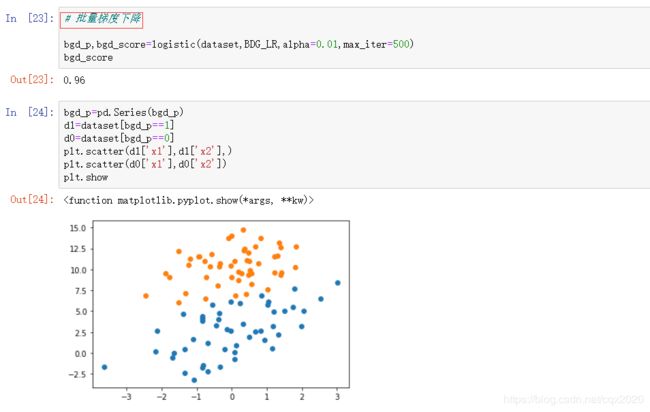
# 主函数1：BDG算法，批量梯度下降

def BDG_LR(dataset,alpha=0.001,max_iter=500):
    #dataset:带标签的数据集，df格式
    #返回：weights各特征权重值w
    
    xmat=np.mat(dataset.iloc[:,:-1].values)
    ymat=np.mat(dataset.iloc[:,-1].values).T
    
    xmat=normalizer(xmat)
    n,m=xmat.shape
    
    weights=np.zeros((m,1))
    for i in range(max_iter):
        grad=xmat.T*(xmat*weights-ymat)/n  #参考批量梯度下降法求解公式，关键的一步
        weights=weights-alpha*grad
    return weights

# 主函数2：SGD算法，随机梯度下降

def SGD_LR(dataset,alpha=0.001,max_iter=500):
    #dataset:带标签的数据集，df格式
    #返回：weights各特征权重值w
    dataset=dataset.sample(max_iter,replace=True)
    dataset.index=range(max_iter)
   
    xmat=np.mat(dataset.iloc[:,:-1].values)
    ymat=np.mat(dataset.iloc[:,-1].values).T
    
    xmat=normalizer(xmat)
    n,m=xmat.shape
    
    weights=np.zeros((m,1))
    for i in range(n):
        grad=xmat[i].T*(xmat[i]*weights-ymat[i]) #关键的一步
        weights=weights-alpha*grad
    return weights

# 主函数3：封装以上函数，便于调用

def logistic(dataset,method,alpha=0.01,max_iter=500):
    #返回：p是分类标签，score是准确率accuracy
    weights=method(dataset,alpha=alpha,max_iter=max_iter)    
    
    xmat=np.mat(dataset.iloc[:,:-1].values)
    xmat=normalizer(xmat)
    
    p=sigmoid(xmat*weights).A.flatten()
    for i,j in enumerate(p):
        if j<0.5:
            p[i]=0
        else:
            p[i]=1

    y_ture=dataset.iloc[:,-1]
    y_pre=pd.Series(p)
    score=(y_ture==y_pre).mean()

    return p,score

四、Python调包实现

from sklearn.linear_model import LogisticRegression as LR
# 关键参数
'''
LR(
    penalty='l2',
    tol=0.0001,
    C=1.0,
    solver='warn',
    max_iter=100,
    multi_class='warn',
)
'''

五、附调用手写函数

参考：http://edu.cda.cn/course/966