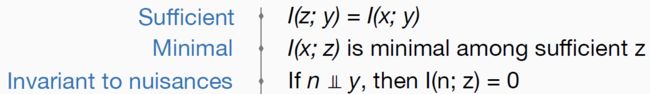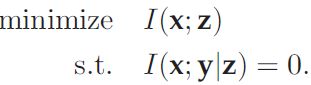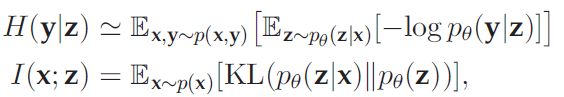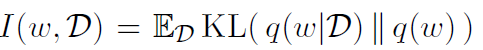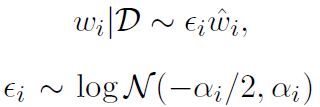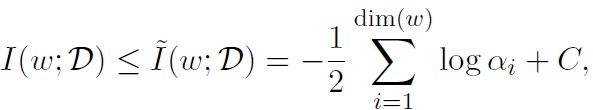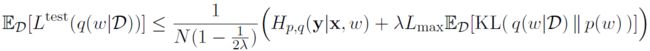Information Bottleneck阅读笔记

DeepBayes暑期学校的最后一讲《Information,  Noise and Emergent  Properties of  Learning Deep  Representations》，邀请的UCLA的Alessandro Achille远程授课，结果这位意大利小哥的英语真是令人迷醉（也许是skype的音质问题？），只看视频完全不知道在讲什么，youtube的自动字幕也经常表示听不懂（没有字幕）。信息瓶颈好像非常重要，一种说法是认为可以用来解释深度神经网络，Hinton更把它誉为深度学习近几年的重大突破。但是看了几页暑期学校的ppt，感觉比较简略，就打算去看看论文搞搞清楚。

这个ppt主要涉及了Achille的三篇论文：

[1] Alessandro Achille, Stefano Soatto: Information Dropout: Learning Optimal Representations Through Noisy Computation. IEEE Trans. Pattern Anal. Mach. Intell. 40(12): 2897-2905(2018)

[2] Alessandro Achille, Stefano Soatto: Emergence of Invariance and Disentanglement in Deep Representations. Journal of Machine Learning Research 19 (2018)

[3] Alessandro Achille, Matteo Rovere, Stefano Soatto: Critical Learning Periods in Deep Neural Networks. CoRR abs/1711.08856 (2017)

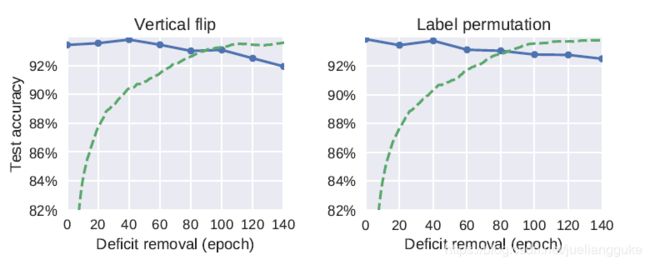
这三篇论文其实是按时间顺序来组织的。其中前两篇论文分别在16、17年就出现在arXiv了，与BI的联系比较紧密。最后一篇是Achille与一个搞神经科学的人合作的，全文通过实验，揭示了神经网络的学习过程与动物的学习过程的一些相似之处，即都有一个Critical Periods。如果在这个时期对学习进行一些阻碍，比如把猫的一只眼蒙上，将CNN的输入图片变得模糊，就会使最终学习到的结果收到严重影响。例如下图左上角的蓝线所示，（CNN在CIFAR10上的结果）40epoch后再消除阻碍，最终的测试准确率就会明显下降。左下角的图，绿线是说从某个epoch开始，对输入进行40个epoch的阻碍，测试集下降的程度。红线没看到明确说明，应该是normalized后的下降。可以观察到左右两种学习环境上Critical Periods的相似性。

但是，如果是对数据进行high-level的扰动，例如垂直翻转、重排标签等处理，并没有一个会使最终模型效果明显下降的Critical Periods。作者也做了ResNet与全连接网络在MNIST两种实验，也有类似地Critical Periods。但网络越深收到的影响越大。

还有一个有趣的实验，作者发现对于输入图片模糊化这个阻碍，如果阻碍持续到很晚，那么就会改变不同NN层的信息量分布（下图中主要是layer6），但如果在更早的时候去掉阻碍(40 epoch)，则不会影响最终分布。作者认为这是因为此时处于consolidation阶段的初期，NN比较敏感所致。而high-level的扰动不会影响信息量的分布。作者认为由于低级的阻碍破坏了低级特征，模型需要分配给高层网络更多信息以学习高级特征。

那么什么是consolidation阶段呢？论文中的另一幅图给出了答案（蓝线对应fisher信息）：

 

fisher信息具体有什么用呢？这个要从前两篇论文中获得答案了。

 

在介绍另外两篇论文之前，我先总体说下看完这些材料后我对信息瓶颈（IB）的理解。对于输入x和标签y，神经网络在学习的过程中很可能记住了x中与y无关的信息，例如把一张图片分为一直狗，图片的背景是没有信息量的，如果可以使神经网络模型舍弃掉这些无关的信息，只学习有关的信息，就可以得到更好的表示，防止出现过学习。信息瓶颈的意思是，如果限制信息流过神经网络层的总量，那么为了更好地预测目标，网络会逐步丢弃掉无关的信息，进而得到更好的表示。限制网络的信息量，用信息论的公式描述就是，输入网络的互信息尽可能小I(M;x)。而[1][2]分别从两个方面将信息瓶颈引入到神经网络里，一是作用在隐层z，即I(z;x)；一是直接作用在网络参数w上，即I(w;x)。我们即将看到，这一项被解释为正则化项，而信息瓶颈视角下的模型目标函数也可以和贝叶斯神经网络的变分下界建立密切的联系。

先看论文[1]，他针对的是神经网络对输入x给出的激活表示z。作者使用了[4]（最早提出IB的论文）[5]两篇论文中提出的理想的z需要的三个性质：

第一项，充分性，目的是让表示z含有所有x中关于y的信息。第二项，就是信息瓶颈的限制项了，希望z中所含x的信息总量最少，当然在满足充分性的前提下。第三项意思就是z中不能含有与y无关的信息。由等式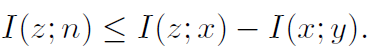，我们可以将寻找满足前两项的z转化为以下优化问题：

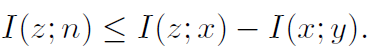[4]中证明了它可以转化为以下形式(Information  Bottleneck  Lagrangian)：。[2]中证明了一个命题，而I(x;y)为常数，因此I(x;z)是I(z;n)的一个上界，只要minimal得到满足，invariant也可以得到满足（原文又稍加解释认为二者是iff的关系）。因此优化IBL就可以满足这三个目标。但[4]只给出了离散情况下的优化算法，对于高维连续分布z，由于边际分布p(z)是intractable的，所以没有闭式解。作者转而把x->z的变换限制为一个noise层。这就类似dropout了。其实在ppt的一开始，作者从信息论视角介绍了数据压缩的方法，一是降维，例如max-pooling；一是升维，例如Dropout,  batch-normalization。这里作者使用了加噪升维的方法来压缩表示，这样做的一个好处是可以使得IBL问题可以被近似，进而进行求解。

    观察最后的式子中的两项：

p(z)此时不是bnn中的先验，而是x编码为z后z的边际分布，是无法求的。为了解决这个问题，作者此时又提出了第四个z的优化目标,disentanglement！就是z的各个分量应该独立，形式化来说就是：。其中q(z)是z的联合分布。这个量全名total correlation。然后作者证明了如下结论：

假设p(z)各分量独立就等于在优化IBL啊！太好了，现在这个目标函数可以求了。可是怎么感觉，这推导了一大圈，回到了full factorized Gaussian为先验的bnn的变分ELBO了。。。哦，还不一样，这里q的参数事业要在学习中被优化的，这在贝叶斯推断里面叫做emprical Bayes。但这里作者是从信息论和优化的角度推出优化目标函数的，这些分布也不能看做先验、后验。这就是殊途同归吧，数学很奇妙。    

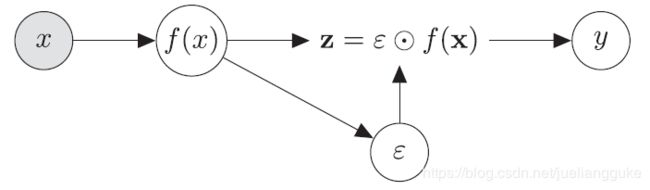
    其实[1]的故事讲到这里就完了，具体p(z|x)和q(z)怎么选，其实和variational dropout[6]是基本一样的。不过这里相当于将激活层随机变量化，[2]才是将模型参数随机变量化，那时才真正等价于variational dropout。

 

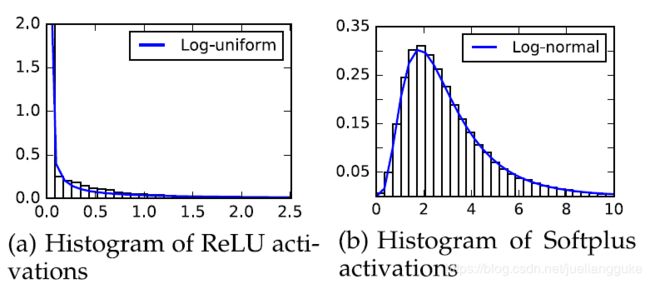
    如上图所示，就是对激活层加一个multiplicative的噪声。激活函数选用了ReLU以及它的光滑近似softplus。由于ReLU具有伸缩不变性，为了使得先验也具有伸缩不变性，这里仍然只能分别选log-uniform。对softplus则选取log-normal作为先验。噪声的分布则为均值为0，方差与输入相关的log-normal。（我觉得这其实又和bnn的另一篇论文联系起来了，[7]为了实现神经网络的结构稀疏化，把bnn中的先验与近似后验都选为log-normal。）有意思的一点是，作者将两种激活函数作用下激活层的直方图可视化后发现分别和两种先验分布非常相浮。

 

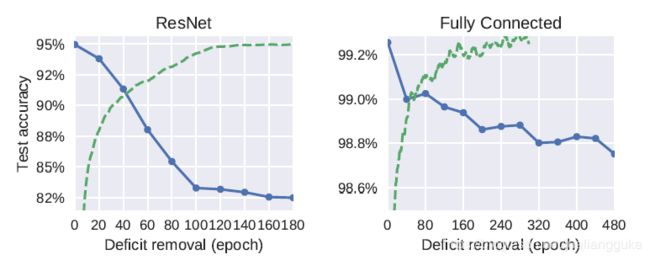
[2]中边边角角的证明比较多，比如上面提到的关于invariant的证明，以及层数堆得越多，对应的z的不变性越强。但它的出发点更加明确，实验结论也比较有趣。关于神经网络一直有一个问题困扰着大家，我们很难通过增加网络参数观察到过拟合的现象。如下图左所示，网络参数数量从1M增加到10M，test error只下降了0.2%左右。作者提出一种观点，参数数量不能真正衡量神经网络的复杂程度，真正起这个作用的是网路参数w中所含输入的信息量，即I(w;x)！所以这次作者的目标是将信息瓶颈的四个限制放在NN参数w上，得到一个类似的优化目标：

推出这个目标的主要依据是H(y|x,w)做了一个巧妙的分解：

等式右边这么多项深切怀疑是作者反着凑出来的。这里假设theta是控制生成数据的参数，{x,y}是从生成数据的分布中采样得到的。第一项，生成数据过程中导致的误差，模型改变不了。第二项，可以看做w中所没有包含的关于y的信息量，最小化它就是最大化sufficiency，没问题。第三项，是让我们的模型预测出的分布与真实的分布接近。最后一项有个符号，所以优化中最最大化它。这一项却是给定了输入后w还含有的关于y的信息量，这些信息很明显就是过学习得到的了。那么，控制这部分信息量很简单，但cross entropy的loss加上这一项就行了。但别急，这一项是没法求的，作者说求它和学习模型难度是一样的。作者用了一个我没太看明白的说法（也没有证明，感觉这个地方很重要啊）就把最后一项放缩到I(w;D)了。大概意思是 的上界是常数，而与模型看到的样本数呈线性关系，所以我们可以转而按如下方式正则化NN：

再由以下两个式子：

我们就把loss放缩到了IBL的形式。

其中p为任意分布，令p是FFG，就和[1]完全一样了。与[6]不同的是，作者这里q选择的噪声是log-normal的：

并用以下式子估计参数中的信息量：

这时，我们可以通过控制beta来控制参数中的信息量，即模型的复杂度。上面右边那个图就是展示了beta过大或过小会使得模型欠学习或过学习。这比模型参数的确更有说服力。

    最后还有两个理论上很重要的点。一是根据PAC-Bayes bounds理论，

就是优化我们的IBL相当于优化测试loss的一个上界。由于这里使用了log-uniform，KL中有个常数无法确定，因此这个上界没有意义。作者称[8]使用Gaussian先验与后验，得到了一个有意义的PAC-Bayes bound。

    二是作者证明了一个Emergence Bound:

这样最小化参数中的信息量，相当于在改善激活层z的四个目标的后三个。这就把两种方法统一起来了，很漂亮。

 

关于前面提到的fisher信息矩阵和信息瓶颈的关系，改日进一步学习后专门再写。事实上与这几篇论文关系不大。

 

[4] Tishby, Naftali, Fernando C. Pereira, and William Bialek. "The information bottleneck method." arXiv preprint physics/0004057 (2000).

[5] Visual representations: defining properties and deep approximations

S Soatto, A Chiuso ICLR16

[6] Diederik P. Kingma, Tim Salimans, Max Welling: Variational Dropout and the Local Reparameterization Trick. NIPS 2015: 2575-2583

[7] Kirill Neklyudov, Dmitry Molchanov, Arsenii Ashukha, Dmitry P. Vetrov:

Structured Bayesian Pruning via Log-Normal Multiplicative Noise. NIPS 2017: 6778-6787

[8] Gintare Karolina Dziugaite, Daniel M. Roy: Computing Nonvacuous Generalization Bounds for Deep (Stochastic) Neural Networks with Many More Parameters than Training Data. UAI 2017