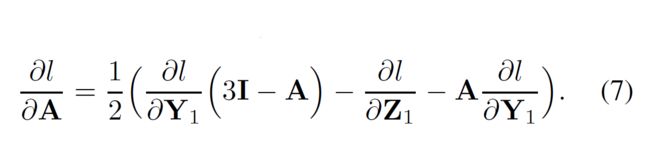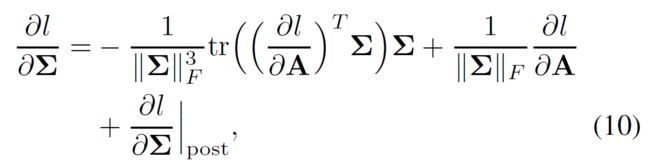CVPR2018论文阅读-Faster MPN-COV：迭代计算矩阵平方根以快速训练全局协方差池化

论文地址 ：Towards Faster Training of Global Covariance Pooling Networks by Iterative Matrix Square Root Normalization
工程地址：github 链接

深层卷积神经网络在计算机视觉的许多领域都获得了很大成功，这个网络实际上可以看成是学习和表示的过程，即经过层次化的卷积以及池化来学习图像特征，最后经过一个全局平均池化得到一个图像层面的表示，然后送给分类器进行分类。
该论文系列的工作重点关注最早在ICLR2014上提出的现在已经广泛的应用于主流的深层网络的全局平均池化，但是全局平均池化的问题在于，网络经过不断地学习得到一个表达能力很强的feature，但是最后在表示这个图像的时候却做了一个全局的均值，统计意义上来讲均值知识一阶的信息，这就让人困惑，为什么不能选择表达能力更强的表示呢？
基于这样的思考，论文作者团队提出了用一个二阶甚至高阶的统计方法来替换一阶的全局平均池化，即将一阶的均值替换为二阶的协方差，幂值取经验值0.5，解决了小样本高纬度难以统计的问题并且有效利用了协方差矩阵的几何结构，系列工作包括先前的CVPR2016(数学理论的推导和验证)，ICCV2017(首次在大规模图像识别中使用并性能优异)，以及CVPR2018也就是此次阅读的论文的迭代计算矩阵平方根提升速率。{2019-4-16刚放出来系列工作的最新进展-Deep CNNs Meet Global Covariance Pooling:Better Representation and Generalization}

0. 摘要

  卷积神经网络中使用全局协方差池化在许多任务上取得了显著的效果，但是特征值分解(EIG)和奇异值分解(SVD)在由于GPU缺乏对其的支持导致这种方法训练缓慢，为了解决这个问题，改论文提出使用迭代式的矩阵平方根算法来快速地对全局协方差矩阵池化进行端到端的训练。本质上，论文提出的方法是一个带有循环嵌套的有向图的元层(meta-layer)，这个元层由三个连续的层组成，分别进行预正则化，牛顿-舒尔茨迭代和后补偿处理。该方法比之前基于EIG或者SVD计算矩阵平方根的方法快很多，因为方法中仅仅包含矩阵乘法，适合并行能力较强的GPU进行运算。而且论文提出的方法应用于ResNet能够加速ResNet的收敛从而加速网络训练，论文提出的方法在几个通用数据集上都取得了SOTA效果。

1. 介绍& 2. 相关工作

  略

3. iSQRT-COV Network

  论文这一节首先概述文章提出的iSQRT-COV网络，然后解释了矩阵平方根的计算和正向传播，最后推导对应的梯度后向传播。

3.1 Overview of Method

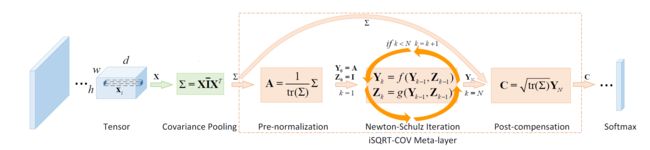
  论文提到的方法的流程如上图所示，卷积层(带有ReLU)输出一个$h\times w\times d$的张量，将这个张量调整为一个维度为d特征数为$n=wh$特征矩阵X，然后通过$\sum =X\bar{I}{X}^T$计算协方差矩阵应用二阶的池化，其中$\bar{I}=\frac{1}{n}(I-\frac{1}{m}1)$，而且I和1分别是$n\times n$的单位矩阵和全是1的矩阵。
  论文提出的meta-layer{循环嵌套的有向图结构}包含三个层，第一层(pre-normalization)将协方差矩阵按照它的迹或者F-范数进行划分以保证下一个阶段的牛顿-舒尔茨迭代的可收敛性，第二层则是一个循环结构，进行一定次数的耦合矩阵方程迭代以计算合适的矩阵平方根，第一层大幅调整了输入数据的量级，所以设计第三层的时候需要乘上平方根矩阵的迹。meta-layer的输出是一个对称矩阵，论文将这个矩阵的上三角区连成一个$d(d+1)/2$维的向量，并将其交付后续卷积网络。

3.2 矩阵平方根和正向传播

  矩阵特别是协方差矩阵的平方根都是正定矩阵，正定矩阵能够通过EIG或者SVD计算一个唯一的平方根，给定A为一个正定矩阵，其EIG可以写作$A=Udiag({\lambda }_i)U^T$，其中U是一个正交矩阵，$diag({\lambda }_i)$是A的特征值组成的对角矩阵，则A的一个平方根就是$Y=Udiag({\lambda }_i^{1/2})U^T$，而且有$Y^2=A$。
牛顿舒尔茨迭代
  一种计算矩阵平方根的方法，为了计算A的平方根Y，假定对于$k=1,...,N，Y_0=A，Z_0=I$，则耦合迭代可以写成如下形式：
$$Y_k=Y_{k-1}{p}_{lm}(Z_{k-1}{Y}_{k-1})q_{lm}(Z_{k-1}{Y}_{k-1}{)}^{-1}$$

$$Z_k=p_{lm}(Z_{k-1}{Y}_{k-1})q_{lm}(Z_{k-1}{Y}_{k-1}{)}^{-1}{Z}_{k-1}\text{\hspace{1em}(1)}$$

  其中$q_{lm}和p_{lm}$是多项式，$l和m$是非负整数，公式1局部收敛：如果||A-I||<1{$||\cdot ||$表示一致矩阵的范数}，则$Y_k$和$Z_k$收敛至Y和Y${}^{-1}$。该族迭代中之前的小误差不会得到放大。当$l=0,m=1$时称迭代为牛顿-舒尔茨迭代，此时与论文的目的即没有GPU不友好型的矩阵的逆的计算：
$$Y_k=\frac{1}{2}{Y}_{k-1}(3I-Z_{k-1}{Y}_{k-1})$$

$$Z_k=\frac{1}{2}(3I-Z_{k-1}{Y}_{k-1})Z_{k-1}\text{\hspace{1em}(2)}$$

  公式2中只涉及矩阵乘法，适合GPU上的并行计算，与通过EIG方法计算的精确的矩阵平方根相比，这种方法仅需要几次迭代就能得到一个较为准确的解，通过交叉验证的方法设置一个迭代次数N，与EIG或者SVD相比，实验表明这种方法得到了相同甚至略优的结果，迭代次数不超过5次。
正规化预处理和补偿式后处理 牛顿-舒尔茨迭代知识局部收敛通过对协方差矩阵进行如下处理{除以迹或者F-范数}：
$$A=\frac{1}{tr(\Sigma )}\Sigma 或者\frac{1}{||\Sigma |{|}_F}\Sigma$$

  设${\lambda }_i$为$\Sigma$的特征值，则$tr(\Sigma )={\Sigma }_i{\lambda }_i，||\Sigma |{|}_F=\sqrt{{\Sigma }_i{\lambda }_i^2}$。而且可以看出$||\Sigma -I|{|}_2$等于$1-\frac{{\lambda }_i}{{\Sigma }_i{\lambda }_i}或者1-\frac{{\lambda }_1}{\sqrt{{\Sigma }_i{\lambda }_i^2}}$，和最大奇异值$\Sigma -I$相等，都小于1，所以收敛条件是满足的。
  以上对协方差矩阵的处理会降低数据的数量级，从而对网络有负面的影响，由此在牛顿舒尔茨迭代后需要根据预处理的操作进行一次后处理，即：
$$C=\sqrt{tr(\Sigma )}{Y}_N或者C=\sqrt{||\Sigma |{|}_F}{Y}_N\text{\hspace{1em}(4)}$$

  另一个可选的后处理方式就是Batch Normlization(BN)，甚至不加任何后处理方式，但是论文的实验表明不叫后处理ResNet无法收敛，使用BN后处理话比论文提到的后处理会降一个百分点。

3.3 反向传播(BP)

  各个层的梯度是通过矩阵反向传播实现的，它建立在一阶泰勒公式的基础上，论文该节以使用矩阵的迹的预处理对相应的梯度进行说明。
后处理的BP 给定$\frac{\partial l}{\partial C}$，$l$是损失函数，根据链式法则，$tr((\frac{\partial l}{\partial C}{)}^{T}dC)=tr((\frac{\partial l}{\partial Y_N}{)}^d{Y}_N+(\frac{\partial l}{\partial \Sigma }{)}^{T}d\Sigma )$，经过一系列计算有：
$$\frac{\partial l}{\partial Y_N}=\sqrt{tr(\Sigma )}\frac{\partial l}{\partial C}$$

$$\frac{\partial l}{\partial \Sigma }{|}_{post}=\frac{1}{2\sqrt{tr(\Sigma )}}((\frac{\partial l}{\partial C}{)}^T{Y}_N)I\text{\hspace{1em}(5)}$$

牛顿-舒尔茨迭代的BP 上一阶段后，计算损失函数关于$\frac{\partial l}{\partial Y_k}$和$\frac{\partial l}{\partial Z_k}$的偏导，其中，k=N-1,…,1，其中$\frac{\partial l}{\partial Y_N}$通过公式5计算，$\frac{\partial l}{\partial Z_N}=0$。因为协方差矩阵$\Sigma$是对称的，所以从公式2可以看出$Y_k和Z_k$都是对称的，根据矩阵后向传播的链式法则和一些列计算，得到当$k=N,...,2$，有：

  最后一步是损失函数关于A的偏导，计算公式如下：

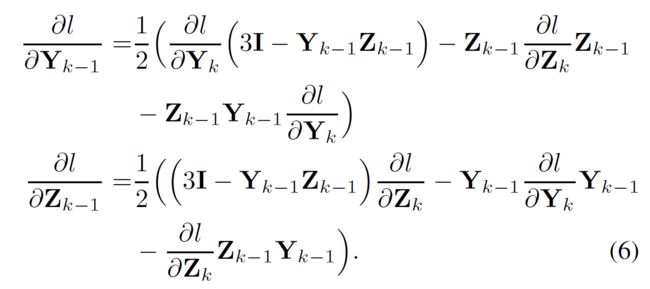
预处理的BP 从后处理层反向传播的信息需要结合损失函数$l$关于协方差矩阵$\Sigma$的梯度，根据公式3，可以得到：

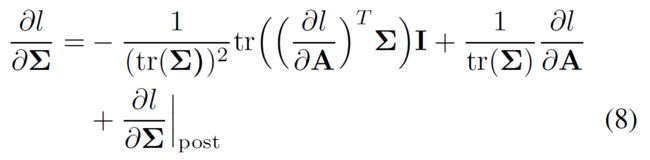
  如果预处理采用F-范数的话，则后处理的梯度变为：

  响应的预处理阶段损失函数关于协方差矩阵的梯度可以写为：

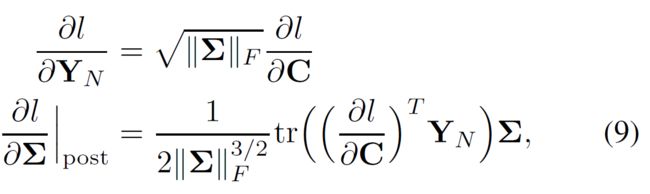
  同时公式6中计算的牛顿-舒尔茨迭代的后向梯度保持不变。
  最终，给定$\frac{\partial l}{\partial \Sigma }$，损失函数$l$关于输入矩阵的梯度可以这样计算：

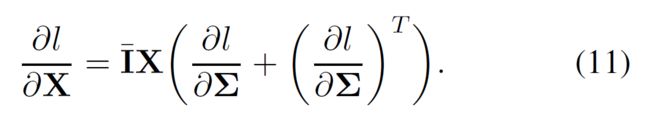
4. 实验

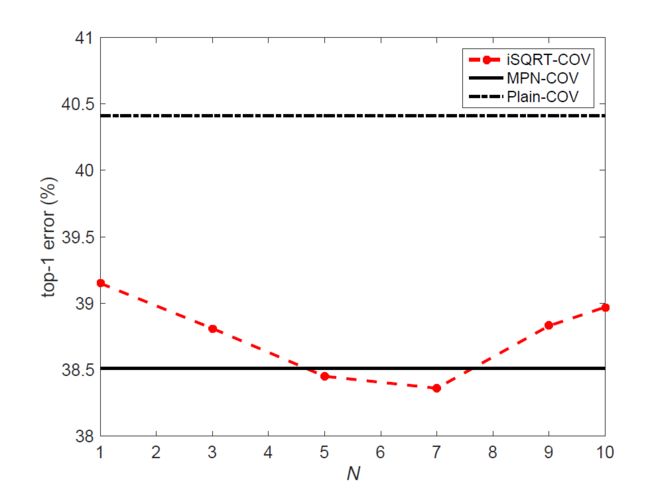
4.1 牛顿-舒尔茨迭代迭代次数对于iSQRT-COV的影响

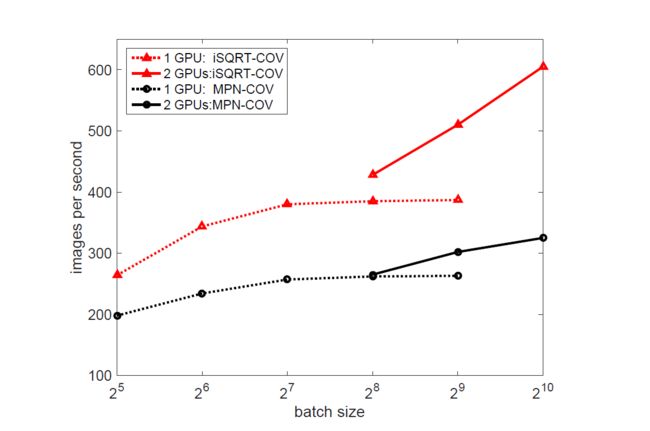
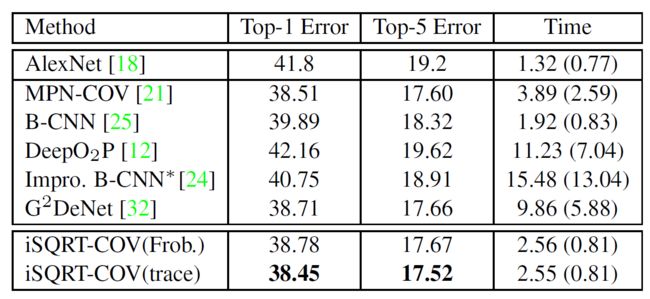
4.2 使用AlexNet架构网络训练的速度

4.3 选择Trace还是Frobenius Norm？

预处理

后处理

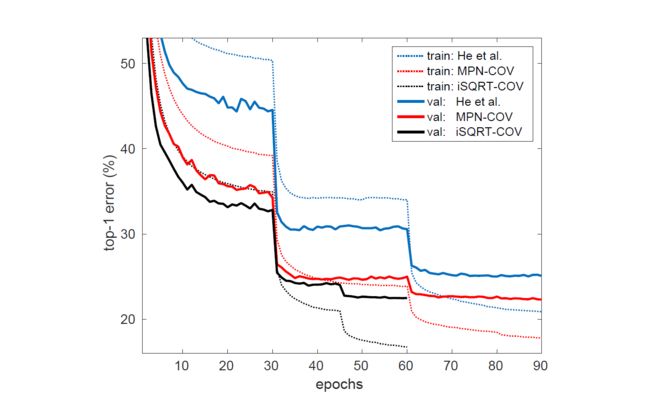
4.4 ResNet架构下不同网络的收敛情况

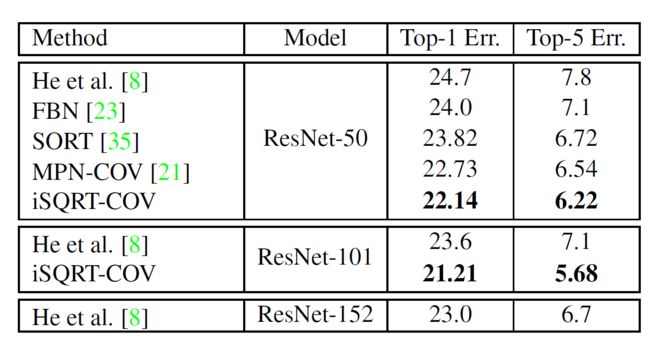
4.5 二阶池化方法和一阶池化方法的对比

5. 结论

  论文提出的通过迭代方法计算矩阵平方根的协方差池化网络iSQRT-COV Network能够进行端到端的训练，通过几次牛顿-舒尔茨迭代使得网络全程在GPU上计算的同时取得了SOTA效果。
  

欢迎扫描二维码关注微信公众号 深度学习与数学   [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读，算法和其他互联网技能的学习，概率论、线性代数等高等数学知识的回顾]