半边数据结构讲解

前言

在介绍半边数据结构之前，必须先要科普一下计算机图形学中，模型的几何表达。

对于一般的几何模型，在计算机图形学上早已有相关的数学模型来表达，而且这些表达已经标准化了。

 

例如对于机械行业的CAD来说，模型是比较规则的，但是要求的精度必须足够精准，所以会有相应的数据结构来表达几何体。例如拉伸体会有对应的特征来表示拉伸体，旋转体会有对应的特征来表示旋转体。而曲面必须要用到nurbs这些精确的数学模型来表达。

而对于数字媒体，游戏，实时交互等的领域，模型通常是不规则的曲面几何体，要求美观（精度低）、计算时间足够短。因此模型通常是用的离散化的表面网格，所谓离散化就是网格通过一系列的面片拼接而成，好像比较粗糙，但是通过贴图和渲染技术可以使得看起来却是光滑的。

 

对于用过OpenGL或者Unity加载和处理过模型的人来说，这些似乎都有些印象，可是这些知识却是在大部分计算机图形学的教材上都是没有或者很少详细介绍的，而这些知识却是非常重要，而且又是非常常用的，因此必须要在这里介绍一下。

 

本文着重介绍离散化的表面网格。

 

对于表面网格来说，其重要的特点在于拓扑，也就是曲面是如何表达的，而不是其顶点的位置。拓扑的不同造就了不同的数据结构和标准，不同的拓扑，其进行网格查询和编辑的性能也不同。

 

在计算机图形学上，有一个术语叫做流形，这是一个比较装逼的术语，很多学术论文都会用到这样一个词。为了这一个词，我还特意学了很久的数学，来看它的数学含义。

现在有经验了，对流形的理解总算有点清晰了。计算机图形学上，通常说的流形是一种几何模型表面（不是所有几何表面都是流形），即二维流形。这种流形在数学上对应的实际上是最简单的流形——拓扑流形。

二维拓扑流形是什么意思呢？二维拓扑流形就是说，流形上的每个点都有一个领域，这个领域能够与欧几里得平面（就是普通意义上的平面）的某个区域一一连续对应。

这是我结合http://blog.csdn.net/lafengxiaoyu/article/details/51524361和点集拓扑的知识总结出的流形的概念。

 

那么二维流形在计算机图形学上的离散化表达是怎样呢？事实上，计算机图形学的流形概念比数学上的流形概念简单多了。简单地说，如果网格的每个边最多被两个面片共用，那么这个网格就是流形网格，否则称为非流形网格。

 

在计算机图形学上，表达表面网格的数据结构有三种，分别是面列表、邻接矩阵、半边结构。

面列表的典型代表是.obj格式文件和Unity。其优点是，简单而且能够表达非流形网格，但网格查询和处理能力差。

当然还有一些不是利用索引，而是直接储存整个顶点的信息，典型代表是OpenGL可编程管线和.stl格式文件。

 

邻接矩阵就不多说了，半边数据结构是接下来要重点讲述的。关于流形网格和这些数据结构的知识可查阅链接: https://pan.baidu.com/s/1jIlCwF8 密码: y9n7

或者https://wenku.baidu.com/view/6424ca78ce2f0066f53322c3.html

 

半边数据结构

关于半边数据结构，其最大特点当然是半边，每个边分为两个半边，每个半边都是一个有向边，方向相反。如果一个边被两个面片共用（正则边），则每个面片都能各自拥有一个半边。如果一个边仅被一个面片占有（边界边），则这个面片仅拥有该边的其中一个半边，另一个半边为闲置状态。

这就能解释为什么半边数据结构仅支持流形网格了。

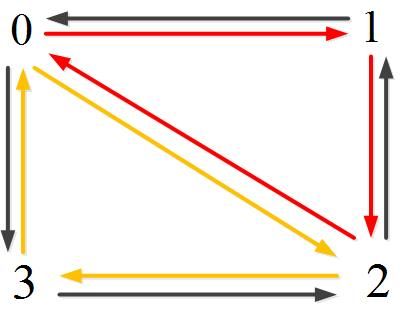
图1

 

下面讲解半边数据结构的三个重要的数据结构——顶点、半边、面片

 

顶点(Vertex)：包含出半边（OutgoingHalfedge）的指针或索引

半边(HalfEdge)：包含起始点（StartVertex）、邻接面(AdjacentFace)、下一条半边(NextHalfedge)、上一条半边(PrevHalfedge)的指针或索引

面片(Face)：包含一条起始边（FirstHalfedge）的指针或索引

 

注意：半边数据结构的面片不一定是三角面片，可以是多边形的面片。

 

对于C/C++的话，所用的应该是指针，此时每个数据结构就变成了链表了。而对于C#或者Java的话，由于没有指针，所以可能要分别增加对应的列表类来容纳各自的点边面。

 

对于C/C++，可参考CGAL或者是OpenMesh，因为它们用的都是半边数据结构。

而C#的话，可参看 https://github.com/meshmash/Plankton的源代码（本文解释用的就是这个接口）。

 

现在问题来了。顶点可能有两条或以上的出半边，而顶点的数据表达只有一条出半边，那这条出半边是哪一条？半边的下一条半边又是哪一条？面片的起始半边又是哪一条？通过某个网格的数据结构图（如图1）能看得出这些信息吗？

 

答：事实上，半边数据结构的网格的构建通常是通过面列表来创建的，也就是说，正常的构建半边数据结构网格是通过一个一个面片的添加来构建的。

所以面的添加顺序就决定了点边面结构的信息，添加面的方法通常是addFace(a,b,c,…)，a,b,c…参数是该面片按其某条环路顺序排列的顶点的指针或索引。注意，环路可以是顺时针或者逆时针，决定了该面片的方向（法向量的方向）。

 

面片的起始半边（FirstHalfedge）：若添加面片的操作为addFace(0,1,2)，那么该面片的起始边为0号指向1号的半边（下面简称0->1，其余以此类推）。

由此可见，面片的起始半边是由顶点的添加顺序决定的，同一个面片（构成其半边的方向也必须相同）的起始半边可以是不同的，因此通过图1是无法知道面片的起始半边是哪条。

 

半边的邻接面(AdjacentFace)：若添加面片的操作为addFace(0,1,2)，则0->1，1->2，2->0的邻接面都是该面片。而1->0，2->1，0->2的邻接面不是该面片。

半边的邻接面是唯一的，若某条边是边界边，则它必定有某条边的邻接面指针为空指针或者索引为-1。所以由图1是能够看出其邻接面的。

 

半边的下一条半边(NextHalfedge)：若添加面片的操作为addFace(0,1,2)，则0->1的下一条边为1->2，也就是说，若该半边是有邻接面的，则其下一条半边沿着邻接面的环路走。如果该半边没有邻接面（边界半边），则其下一条半边沿着边界走（这个后面会解释）。所以由图1是能够看出半边的下一条半边的。

 

顶点的出半边(OutgoingHalfedge)：若该顶点是边界边的顶点，则其出半边必为边界半边，通过图1是能看出的。若该顶点并不是边界边的顶点（被封闭），则其出半边为其被封闭前（添加最后一个面片即被封闭）的出半边，通过图1无法看出。为什么是这样呢？后面会解释。

 

好了，下面通过C#的代码来解释半边网格的构建。

PlanktonMesh pMesh = new PlanktonMesh();
            List vertices = new List();
            vertices.Add(new PlanktonXYZ(-1, 1, 0));
            vertices.Add(new PlanktonXYZ(1, 1, 0));
            vertices.Add(new PlanktonXYZ(1, -1, 0));
            vertices.Add(new PlanktonXYZ(-1, -1, 0));

            pMesh.Vertices.AddVertices(vertices);

            pMesh.Faces.AddFace(0, 1, 2);
            pMesh.Faces.AddFace(0, 2, 3);

核心代码很短，前面都是添加顶点，最关键的就是pMesh.Faces.AddFace方法，下面讲解一下。

 

首先，添加顶点0,1,2构成的面片，代码按顺序成对添加半边(addPair方法)，注意，半边是成对地添加的，即有0->1必有1->0。并分配其邻接面，无邻接面半边其邻接面索引设为-1。

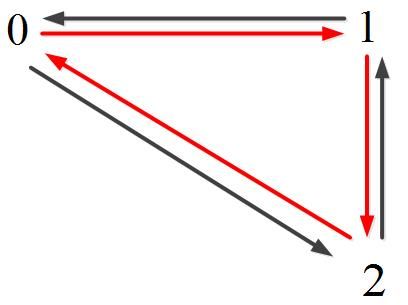
图2

 

此时，

第0条边:0->1，邻接面为0

第1条边:1->0，邻接面为-1

第2条边:1->2，邻接面为0

第3条边:2->1，邻接面为-1

第4条边:2->0，邻接面为0

第5条边:0->2，邻接面为-1

 

然后分配外围半边（非该面的半边）的下一条边和上一条边和顶点的出半边（swich(id)语句之后）：

2->1的下一条边为1->0，1号顶点的出半边为1->0（边界半边）

0->2的下一条边为2->1，2号顶点的出半边为2->1（边界半边）

1->0的下一条边为0->2，0号顶点的出半边为0->2（边界半边）

上一条半边信息从下一条半边的信息可知。

0->2，2->1，1->0构成一个环，满足边界环路。

 

然后分配该面的半边的下一条半边：

0->1下一条半边为1->2

1->2下一条半边为2->0

2->0下一条半边为0->1

0->1，1->2，2->0构成一个环，满足面环路。

 

好了，下面添加另一个面0,2,3

图3

 

现在的情况跟添加第一个面的情况不同，因为0->2已存在，所以只需添加剩余的边即可：

第6条边:2->3，邻接面为0

第7条边:3->2，邻接面为-1

第8条边:3->0，邻接面为0

第9条边:0->3，邻接面为-1

 

由于0->2已经不是边界半边了，2->1的上一条边不再是它，而是3->2。

即3->2的下一条边为2->1

0->3的下一条边为3->2（和第一个面片的情况一样），3号顶点的出半边为3->2（边界半边）

1->0的下一条边改为0->3，0号顶点的出半边改为0->3（边界半边）

从而使得边界环路满足。

 

然后分配该面的半边的下一条半边：

0->2下一条半边为2->3

2->3下一条半边为3->0

3->0下一条半边为0->2

0->2，2->3，3->0构成一个环，满足面环路。

 

好了，下面思考一下，假如第二个面片的顶点添加顺序为addFace(2,0,3)，该面片能否添加成功？

答案是否定的，因为2->0已经存在并且带有邻接面0，不满足面片共享各自半边的条件。

 

好了，假如一个顶点的周围都是面片（不是某个边界边的顶点），如图4所示，0号顶点的出半边是哪条？

 

图4

 

核心代码如下：

            PlanktonMesh pMesh = new PlanktonMesh();
            List vertices = new List();
            vertices.Add(new PlanktonXYZ(0, 0, 0));
            vertices.Add(new PlanktonXYZ(0, 1, 0));
            vertices.Add(new PlanktonXYZ(1,-1, 0));
            vertices.Add(new PlanktonXYZ(-1,-1,0));

            pMesh.Vertices.AddVertices(vertices);

            pMesh.Faces.AddFace(0, 1, 2);
            pMesh.Faces.AddFace(0, 2, 3);
            pMesh.Faces.AddFace(0, 3, 1);

 

注意，当还未执行语句pMesh.Faces.AddFace(0,3, 1);的时候，0号顶点的出半边为0->3。执行完之后，如果0号顶点不封闭，则它的出半边本应改为0->1，可是0->1早已存在。故0号顶点的出半边不会再改变，仍为0->3。

 

 

好了，半边数据结构的讲解就到此为止了。当然了，如果要在OpenGL或Unity中显示半边数据结构，则必须要把半边数据结构的数据转换为相应的网格数据。这个不难，只要熟悉OpenGL和Unity即知道如何转换。可以提醒一下，由于OpenGL和Unity的顶点数据都是用数组来传递的，因此必须把半边数据结构的顶点列表转换成坐标的数组，这个是不难的。C/C++的话可以搜索一下OpenMesh+OpenGL的教程。C#的话可以搜索Unity读取.obj文件/.stl文件的教程，或者直接搜索半边数据结构+Unity的教程即可。

 

最后分享一下本人添加注释的C#源代码，重点看PlanktonFaceList.cs的代码

链接：http://pan.baidu.com/s/1qXZoY5Y 密码：vder