leetcode_位运算
文章目录
- 原理
- 基本原理
- 位与运算技巧
- 移位运算
- mask 计算
- Java 中的位操作
- 461. 汉明距离
- 136. 只出现一次的数字
- 268. 缺失数字
- 260. 只出现一次的数字 III
- 190. 颠倒二进制位
- 不用额外变量交换两个整数
- 231. 2的幂
- 342. 4的幂
- 693. 交替位二进制数
- 476. 数字的补数
- 371. 两整数之和
- 318. 最大单词长度乘积
- 338. 比特位计数
- 小总结
原理
基本原理
0s 表示一串 0,1s 表示一串 1。
x ^ 0s = x x & 0s = 0 x | 0s = x
x ^ 1s = ~x x & 1s = x x | 1s = 1s
x ^ x = 0 x & x = x x | x = x
利用 x ^ 1s = ~x 的特点,可以将一个数的位级表示翻转;利用 x ^ x = 0 的特点,可以将三个数中重复的两个数去除,只留下另一个数。
112 = 2
利用 x & 0s = 0 和 x & 1s = x 的特点,可以实现掩码操作。一个数 num 与 mask:00111100 进行位与操作,只保留 num 中与 mask 的 1 部分相对应的位。
01011011 &
00111100
--------
00011000
利用 x | 0s = x 和 x | 1s = 1s 的特点,可以实现设值操作。一个数 num 与 mask:00111100 进行位或操作,将 num 中与 mask 的 1 部分相对应的位都设置为 1。
01011011 |
00111100
--------
01111111
位与运算技巧
n&(n-1) 去除 n 的位级表示中最低的那一位 1。例如对于二进制表示 01011011,减去 1 得到 01011010,这两个数相与得到 01011010。
01011011 &
01011010
--------
01011010
n&(-n) 得到 n 的位级表示中最低的那一位 1。-n 得到 n 的反码加 1,也就是 -n=~n+1。例如对于二进制表示 10110100,-n 得到 01001100,相与得到 00000100。
10110100 &
01001100
--------
00000100
n-(n&(-n)) 则可以去除 n 的位级表示中最低的那一位 1,和 n&(n-1) 效果一样。
移位运算
>>n 为算术右移,相当于除以 2n,例如 -7 >> 2 = -2。
11111111111111111111111111111001 >> 2
--------
11111111111111111111111111111110
>>>n 为无符号右移,左边会补上 0。例如 -7 >>> 2 = 1073741822。
11111111111111111111111111111001 >>> 2
--------
00111111111111111111111111111111
<< n 为算术左移,相当于乘以 2n。-7 << 2 = -28。
11111111111111111111111111111001 << 2
--------
11111111111111111111111111100100
mask 计算
要获取 111111111,将 0 取反即可,~0。
要得到只有第 i 位为 1 的 mask,将 1 向左移动 i-1 位即可,1<<(i-1) 。例如 1<<4 得到只有第 5 位为 1 的 mask :00010000。
要得到 1 到 i 位为 1 的 mask,(1< 要得到 1 到 i 位为 0 的 mask,只需将 1 到 i 位为 1 的 mask 取反,即 ~((1< 两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。 示例: 题解:布赖恩·克尼根算法 int类型的数最多为32位,因此时间复杂度为O(1), 空间复杂度为O(1) 给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 示例 1: 示例 2: 题解:异或运算 时间复杂度O(n) 给定一个包含 0, 1, 2, …, n 中 n 个数的序列,找出 0 … n 中没有出现在序列中的那个数。 示例 1: 示例 2: 题解:异或运算 时间复杂度O(n) 给定一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。 示例 : 注意: 题解:异或运算 颠倒给定的 32 位无符号整数的二进制位。 示例 1: 示例 2: 提示: 请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。 进阶: 题解: 时间复杂度:O(1) 2. 按比特块交换 图片来源:力扣(LeetCode) java代码: 时间复杂度O(1) 程序员代码面试指南 :P317 给定一个整数,编写一个函数来判断它是否是 2 的幂次方。 示例 1: 示例 2: 示例 3: 题解 给定一个整数 (32 位有符号整数),请编写一个函数来判断它是否是 4 的幂次方。 示例 1: 示例 2: 进阶: 题解:位操作 4的幂次方就是2的偶数次方: 时间复杂度O(1) 给定一个正整数,检查他是否为交替位二进制数:换句话说,就是他的二进制数相邻的两个位数永不相等。 示例 1: 示例 2: 示例 3: 示例 4: 题解: 2. 错位不相同 给定一个正整数,输出它的补数。补数是对该数的二进制表示取反。 示例 1: 示例 2: 注意: 给定的整数保证在 32 位带符号整数的范围内。 题解: 不使用运算符 + 和 - ,计算两整数 a 、b 之和。 示例 1: 示例 2: 题解 给定一个字符串数组 words,找到 length(word[i]) * length(word[j]) 的最大值,并且这两个单词不含有公共字母。你可以认为每个单词只包含小写字母。如果不存在这样的两个单词,返回 0。 示例 1: 示例 2: 示例 3: 题解:位运算 时间复杂度O(n^2) 给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回。 示例 1: 示例 2: 输入: 5 给出时间复杂度为O(n*sizeof(integer))的解答非常容易。但你可以在线性时间O(n)内用一趟扫描做到吗? 题解: 时间复杂度O(kn) 时间复杂度O(n)Java 中的位操作
static int Integer.bitCount(); // 统计 1 的数量
static int Integer.highestOneBit(); // 获得最高位
static String toBinaryString(int i); // 转换为二进制表示的字符串
461. 汉明距离
给出两个整数 x 和 y,计算它们之间的汉明距离。
注意:
0 ≤ x, y < 231.输入: x = 1, y = 4
输出: 2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
n = x^y, n中1的个数即为x与y的相同的位数。n&(n-1) 运算可将n最右边的1去掉,不断更新n至n为0,看进行了几次这样的计算1的个数就为几个。# 布赖恩·克尼根算法
class Solution:
def hammingDistance(self, x: int, y: int) -> int:
cnt = 0
n = x^y # 不同为1,相同为0,然后在计算n中1的个数
while n:
cnt += 1
n = (n-1) & n
return cnt
136. 只出现一次的数字
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?输入: [2,2,1]
输出: 1
输入: [4,1,2,1,2]
输出: 4
异或运算有如下性质:
0^a=aa^a=0a^b^b^c^c=a
因此只要将数组中所有元素做异或运算,最后的结果即为只出现一次的元素class Solution:
def singleNumber(self, nums: List[int]) -> int:
x = 0
for num in nums:
x ^= num
return x
空间复杂度O(1)
268. 缺失数字
输入: [3,0,1]
输出: 2
输入: [9,6,4,2,3,5,7,0,1]
输出: 8
将数组中的元素以及0,1,2...,n做异或运算,除了缺失的数只有一个,其他数都有两个,因此结果为缺失的数。class Solution:
def missingNumber(self, nums: List[int]) -> int:
n = len(nums)
for i in range(len(nums)):
n = n ^ i ^ nums[i]
return n
空间复杂度O(1)
260. 只出现一次的数字 III
输入: [1,2,1,3,2,5]
输出: [3,5]
结果输出的顺序并不重要,对于上面的例子, [5, 3] 也是正确答案。
你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现?
n = a^ba^b不相同的那一位,即等于1的那一位,假设是第p位,给数组中的元素分组,第p位等于1的为一组,等于0的为一组,那么相同元素必定分到同一组,a和b分到不同的组,每个组的元素再作异或运算必然分分别得到a和b的值class Solution:
def singleNumber(self, nums: List[int]) -> List[int]:
n = 0
for num in nums:
n ^= num
# 找不同的那一位,即等于1的那一位:
n &= -n # 保留最低位的1
# 根据第p位的数值分成两组,第p位等于1的一组,第p位等于0的一组
# 与p作与运算即可
a = 0
b = 0
for num in nums:
if num & n == 0:
a ^= num
else:
b ^= num
return [a, b]
190. 颠倒二进制位
输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596,
因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000。
输入:11111111111111111111111111111101
输出:10111111111111111111111111111111
解释:输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293,
因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。
在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在上面的 示例 2 中,输入表示有符号整数 -3,输出表示有符号整数 -1073741825。
如果多次调用这个函数,你将如何优化你的算法?
class Solution:
def reverseBits(self, n: int) -> int:
res = 0
for i in range(32):
res = (res<<1) + (n & 1)
n = n>>1
return res
空间复杂度:O(1)
链接:https://leetcode-cn.com/problems/reverse-bits/solution/dian-dao-er-jin-zhi-wei-by-leetcode/
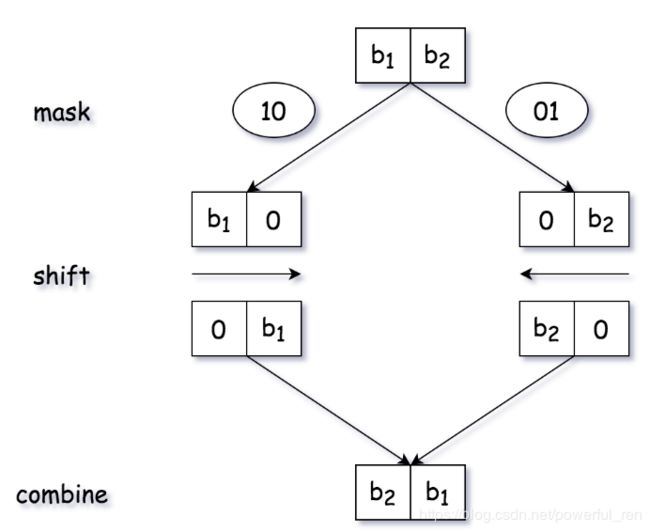
python代码:class Solution:
def reverseBits(self, n: int)->int:
n = ((n & 0xffff0000) >> 16) | ((n & 0x0000ffff) << 16)
n = ((n & 0xff00ff00) >> 8) | ((n & 0x00ff00ff) << 8)
n = ((n & 0xf0f0f0f0) >> 4) | ((n & 0x0f0f0f0f) << 4)
n = ((n & 0xcccccccc) >> 2) | ((n & 0x33333333) << 2)
n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1)
return n;
一定要逻辑右移,也就是三个大于号 >>>,不能考虑符号位,具体就是涉及到 补码 的知识了。public class Solution {
// you need treat n as an unsigned value
public int reverseBits(int n) {
n = ((n & 0xffff0000) >>> 16) | ((n & 0x0000ffff) << 16);
n = ((n & 0xff00ff00) >>> 8) | ((n & 0x00ff00ff) << 8);
n = ((n & 0xf0f0f0f0) >>> 4) | ((n & 0x0f0f0f0f) << 4);
n = ((n & 0xcccccccc) >>> 2) | ((n & 0x33333333) << 2);
n = ((n & 0xaaaaaaaa) >>> 1) | ((n & 0x55555555) << 1);
return n;
}
}
空间复杂度O(1)
不用额外变量交换两个整数
a = a ^ b;
b = a ^ b;
a = a ^ b;
231. 2的幂
输入: 1
输出: true
解释: 20 = 1
输入: 16
输出: true
解释: 24 = 16
输入: 218
输出: false
证明二进制只有一个1:把最低位的1去掉,看是否等于0class Solution:
def isPowerOfTwo(self, n: int) -> bool:
return n>0 and n&(n-1) == 0
342. 4的幂
输入: 16
输出: true
输入: 5
输出: false
你能不使用循环或者递归来完成本题吗?
num > 0 and num&(num-1) == 0
若1在偶数位,则其与偶数位为0,奇数位为1的32位二进制数作与运算必为0。
如若num = 1000, 那么1000 & 0101 = 0class Solution:
def isPowerOfFour(self, num: int) -> bool:
return num > 0 and num&(num-1) == 0 and num& 0xaaaaaaaa == 0
空间复杂度O(1)
693. 交替位二进制数
输入: 5
输出: True
解释:
5的二进制数是: 101
输入: 7
输出: False
解释:
7的二进制数是: 111
输入: 11
输出: False
解释:
11的二进制数是: 1011
输入: 10
输出: True
解释:
10的二进制数是: 1010
1. 逐位判断
比较当前每一个一位与前一位是否相同:(n%2) ^ (n>>1)&1
当前位:n%2,前一位n>>1, 判断是否相同,用异或。class Solution:
def hasAlternatingBits(self, n: int) -> bool:
while n:
if (n%2) ^ (n>>1)&1 == 0:
return False
n = n>>1
return True
temp = n&(n>>1):错位不相同,因此每一位都为1
temp&(temp+1) :判断是否每一位都为1class Solution:
def hasAlternatingBits(self, n: int) -> bool:
temp = n^(n>>1)
return temp&(temp+1) == 0
476. 数字的补数
输入: 5
输出: 2
解释: 5 的二进制表示为 101(没有前导零位),其补数为 010。所以你需要输出 2 。
输入: 1
输出: 0
解释: 1 的二进制表示为 1(没有前导零位),其补数为 0。所以你需要输出 0 。
你可以假定二进制数不包含前导零位。
本题与 1009 https://leetcode-cn.com/problems/complement-of-base-10-integer/ 相同
如num = 101, 111-101 = 010class Solution:
def findComplement(self, num: int) -> int:
cnt = 0
temp = num
while temp !=0 :
cnt += 1
temp = temp >> 1
return ((1<<cnt)-1)^num
如num = 101, 111^101 = 010class Solution:
def findComplement(self, num: int) -> int:
temp = 1
while temp<=num:
temp <<= 1
return temp-1-num
371. 两整数之和
输入: a = 1, b = 2
输出: 3
输入: a = -2, b = 3
输出: 1
考虑有进位和没有进位。
假设 a = 101, b = 111
不考虑进位时,用异或运算:101 ^ 111 = 010
考虑进位时,用与运算: (101 & 111) << 1 = 1010, 左移一位是因为需要更高位为1.
然后将不考虑进位和进位相加,又是两数相加,可迭代操作,直到进位为0.class Solution {
public int getSum(int a, int b) {
while (b != 0){
int temp = a^b; // 不考虑进位
b = (a & b)<<1; // 进位
a = temp;
}
return a;
}
}
318. 最大单词长度乘积
输入: ["abcw","baz","foo","bar","xtfn","abcdef"]
输出: 16
解释: 这两个单词为 "abcw", "xtfn"。
输入: ["a","ab","abc","d","cd","bcd","abcd"]
输出: 4
解释: 这两个单词为 "ab", "cd"。
输入: ["a","aa","aaa","aaaa"]
输出: 0
解释: 不存在这样的两个单词。
每个单词用二进制表示,某字符存在时,对应位置为1
如abc:00000111
如acd: 00001101
当有两个字符串没有相同字符时,对应二进制与运算为0class Solution:
def maxProduct(self, words: List[str]) -> int:
values = [0]*len(words)
for i in range(len(words)):
for alp in words[i]:
values[i] |= 1<<(ord(alp) - 97)
res = 0
for i in range(len(words)):
for j in range(i,len(words)):
if values[i] & values[j] == 0:
res = max(res, len(words[i])*len(words[j]))
return res
空间复杂度O(n)
338. 比特位计数
输入: 2
输出: [0,1,1]
输出: [0,1,1,2,1,2]
进阶:
要求算法的空间复杂度为O(n)。
你能进一步完善解法吗?要求在C++或任何其他语言中不使用任何内置函数(如 C++ 中的 __builtin_popcount)来执行此操作。
计算1的个数的方法用: num &= num-1class Solution {
public int[] countBits(int num) {
int[] res = new int[num+1];
for (int i=1; i<=num; i++){
res[i] = help(i);
}
return res;
}
public int help(int num){
int count = 0;
while (num!=0){
count ++;
num &= num-1;
}
return count;
}
}
空间复杂度O(n)
2. 动态规划+最低有效位
num去掉低位的1为:n = num&(num-1), 则num的1的个数等于n的1的个数+1.
例如6(110), 去掉低位的1为 4(100) ,100中1的个数为1,那么6中1的个数为1+1=2class Solution {
public int[] countBits(int num) {
int[] f = new int[num+1];
for (int i = 1; i<=num; i++){
f[i] = f[i&(i-1)] + 1;
}
return f;
}
}
空间复杂度O(n)小总结
a^b不相同的位,即等于1的那一位可用两种方法:
1作与运算,等于1的那一位即为所求n &= -n可得到n的最低位的1
n&(n-1) == 0n&(n+1) == 0