多普勒微波感应和FMCW微波感应原理以及应用
0. 前言
雷达主要分为多普勒雷达、脉冲雷达、频率调制连续波FMCW雷达。脉冲雷达由于需要贵重的磁体控制脉冲开关，较少使用。多普勒雷达通常只能获得目标速度，而目标距离难以获取。FMCW雷达，
1. 多普勒雷达HB100原理
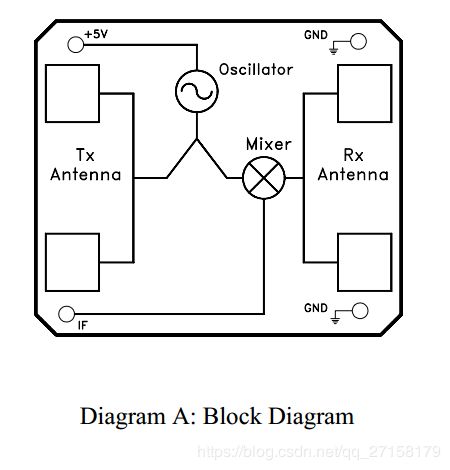
多普勒雷达原理来自多普勒效应。手头上的HB100微波传感器的原理是多普勒测距雷达。规格书上[1]有本模块的方框图。
设发送信号为T(t)，则其函数为：
是发送信号的频率。多普勒雷达中这个频率一般是个固定值。
是初始相位。
不计天线增益和信号衰减，接收天线的获得的信号为：
其中
是发送信号的波长。
。c是光速，约为3x10^8m/s。v是目标的移动速度。
是多普勒频移[4]。而d是目标到微波感应器的距离。
Mixer是T(t)和R(t)的相乘。
根据三角函数关系：
可得：
采用合适截止频率的低通运放电路，即截止频率在
，可以得到输入到ADC模块的信号：
公式中G是运放的增益。模块的规格书说明，输出信号电压幅值和成正比的。
2. HB100的典型应用
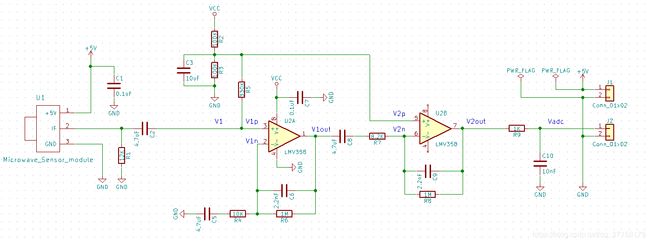
规格书[1]有HB100的典型应用，根据此图，在KiCad上可以绘制出原理图。KiCad的原理图和PCB设计文件已经共享到github。https://github.com/xxJian/HB100_Microwave_Demo
R1作用是假负载。
静态分析：
V1out中由于U2A运放对直流信号没有放大作用，同时没移植作用，故VCC增益不变。
动态分析：
1阶RC电路截止频率计算公式：
| 电阻 | 电容 | 截止频率 |
| R5+R2//R3 |
C2 |
0.09Hz |
| R4 |
C5 |
3.39Hz |
| R6 |
C6 |
72.34Hz |
| R7 |
C8 |
4.13Hz |
| R8 |
C9 |
72.34Hz |
| R9 |
C10 |
16KHz |
3. FMCW雷达
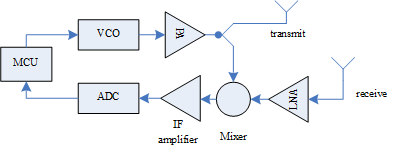
图2. 一款雷达应用的实现框图[5]
MCU是单片机。VCO是压控振荡器，可以通过输入的模拟信号大小而控制输出信号的频率。PA是功率运放。LNA是Low Noise Amplifier的缩写。Mixer把两个信号相乘并输出IF信号。IF amplifier是把IF信号放大，并带有低通滤波的效果。ADC是模拟信号-数字信号转换器。
单发送单接收的FMCW示意图如图3所示。FMCW调制过程中，线性调制信号的上限和下限只差为B，同时这个频率范围有严格规定[2]。24GHz雷达的带宽为200MHz，而77GHz允许有4GHz的带宽范围。
3.1 计算距离
发送信号的频率为ft。fr为接受信号的频率。Td是发送、接收延时。Tc为上升时间。线性调制的斜率为B/Tc。
图3 FMCW示意图
图3中，由相似三角形，可得到以下关系：
而
发送信号的波形函数（Tc时间内）：
而接收信号的时域函数：
混频器的输出时域函数（这里就直接频率相减、相位相减）：
通过FFT得到Mix(t)的频率
，再通过计算即可得到距离d。
3.2 计算速度
时间间距为Tc，先后发送两个线性调制脉冲信号，见下图。
发送信号的波形函数（Tc时间内）：
适当化简：
那么接收信号的时域函数是：
适当化简：
混频器输出：
将Mix1和Mix2再次进行混频（频率相减、相位相减）
4. TODO: TI的mm radar
到TI的官网搜mm radar得到iwr1443 mmware radar……个人认为资料比较丰富了。还有教学视频，但我还没看。
参考资料：
资料[1]：https://www.limpkin.fr/public/HB100/HB100_Microwave_Sensor_Application_Note.pdf
资料[2]：Moving from legacy 24 GHz to state-of-the-art 77 GHz radar, http://www.ti.com/lit/wp/spry312/spry312.pdf
资料[3]：MicrowaveNoncontactMotionSensingandAnalysis.pdf
资料[4]：https://www.school-for-champions.com/science/waves_doppler_effect_wavelength_derivations.htm#.W-JGFbiQOO4
资料[5]：http://hforsten.com/third-version-of-homemade-6-ghz-fmcw-radar.html