【学习笔记】零基础入门CV之街道字符识别-模型训练与验证

本章，我们在简单的CNN模型基础上进行模型训练与验证。

1. 学习目标

• 理解验证集的作用，并使用训练集和验证集完成训练
• 学会使用Pytorch环境下的模型读取和加载，并了解调参流程

2. 验证集

在机器学习模型（特别是深度学习模型）的训练过程中，存在着过拟合与欠拟合的情况。因此模型如果将训练集学的过好，模型就会记住训练样本的细节，导致模型在测试集的泛化效果较差，这种现象称为过拟合（Overfitting）。与过拟合相对应的是欠拟合Underfitting），即模型在训练集上的拟合效果较差。

图1 过拟合与欠拟合
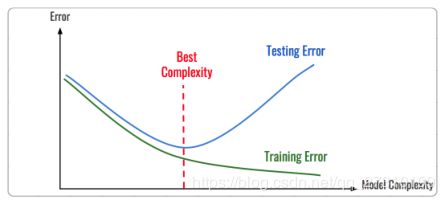
为了解决这个问题，我们一般会把本地数据划分出一个验证集。训练集、验证集和测试集分别有不同的作用：

• 训练集（Train Set）：模型用于训练和调整模型参数；
• 验证集（Validation Set）：用来验证模型精度和调整模型超参数；
• 测试集（Test Set）：验证模型的泛化能力。

验证集的划分方法一般包括以下几种：
（1） 留出法（Hold-Out）
直接将训练集划分成两部分，新的训练集和验证集。这种划分方式的优点是最为直接简单；缺点是只得到了一份验证集，有可能导致模型在验证集上过拟合。留出法应用场景是数据量比较大的情况。

（2） 交叉验证法（Cross Validation，CV）
将训练集划分成K份，将其中的K-1份作为训练集，剩余的1份作为验证集，循环K训练。这种划分方式是所有的训练集都是验证集，最终模型验证精度是K份平均得到。这种方式的优点是验证集精度比较可靠，训练K次可以得到K个有多样性差异的模型；CV验证的缺点是需要训练K次，不适合数据量很大的情况。

（3）自助采样法（BootStrap）
通过有放回的采样方式得到新的训练集和验证集，每次的训练集和验证集都是有区别的。这种划分方式一般适用于数据量较小的情况。

在本次赛题中已经划分为验证集，所以我们可以直接使用训练集进行训练，并使用验证集进行验证精度。

3. 模型训练与验证

接下来，我们使用Pytorch来完成CNN的训练和验证过程，CNN网络结构与之前的章节中保持一致。我们需要完成的逻辑结构如下：

• 构造训练集和验证集；
• 每轮进行训练和验证，并根据最优验证集精度保存模型。

train_loader = torch.utils.data.DataLoader(
    train_dataset,
    batch_size=10, 
    shuffle=True, 
    num_workers=10, 
)
    
val_loader = torch.utils.data.DataLoader(
    val_dataset,
    batch_size=10, 
    shuffle=False, 
    num_workers=10, 
)

model = SVHN_Model1()
criterion = nn.CrossEntropyLoss (size_average=False)
optimizer = torch.optim.Adam(model.parameters(), 0.001)
best_loss = 1000.0
for epoch in range(20):
    print('Epoch: ', epoch)

    train(train_loader, model, criterion, optimizer, epoch)
    val_loss = validate(val_loader, model, criterion)
    
    # 记录下验证集精度
    if val_loss < best_loss:
        best_loss = val_loss
        torch.save(model.state_dict(), './model.pt')

对每个Epoch进行训练：

def train(train_loader, model, criterion, optimizer, epoch):
    # 切换模型为训练模式
    model.train()

    for i, (input, target) in enumerate(train_loader):
        c0, c1, c2, c3, c4, c5 = model(data[0])
        loss = criterion(c0, data[1][:, 0]) + \
                criterion(c1, data[1][:, 1]) + \
                criterion(c2, data[1][:, 2]) + \
                criterion(c3, data[1][:, 3]) + \
                criterion(c4, data[1][:, 4]) + \
                criterion(c5, data[1][:, 5])
        loss /= 6
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

对每个Epoch进行验证：

def validate(val_loader, model, criterion):
    # 切换模型为预测模型
    model.eval()
    val_loss = []

    # 不记录模型梯度信息
    with torch.no_grad():
        for i, (input, target) in enumerate(val_loader):
            c0, c1, c2, c3, c4, c5 = model(data[0])
            loss = criterion(c0, data[1][:, 0]) + \
                    criterion(c1, data[1][:, 1]) + \
                    criterion(c2, data[1][:, 2]) + \
                    criterion(c3, data[1][:, 3]) + \
                    criterion(c4, data[1][:, 4]) + \
                    criterion(c5, data[1][:, 5])
            loss /= 6
            val_loss.append(loss.item())
    return np.mean(val_loss)