AlexNet网络结构分析及pytorch代码

这篇论文在2012年发表，文章中的模型AlexNet，参加的竞赛是ImageNet LSVRC-2010，该ImageNet数据集有1.2 million幅高分辨率图像，总共有1000个类别。测试集分为top-1和top-5，并且分别拿到了37.5%和17%的error rates，CNN重新引起人们的关注。下面就AlexNet做一下简要的分析。也是记录一下今天一天的学习。

AlexNet的特点：

1：AlexNet一共有八层，五个卷积层和三个全连接层。由于是对ImageNet数据集进行分类，所以最后一层的输出会接上softmax，一共1000个输出(ImageNet一共有1000个类别),softmax会产生1000类标签。
2：在AlexNet中，使用RuLu函数来增加模型的非线性能力。
3：使用了Dropout训练期间选择性的暂时忽略一些神经元，来减小模型的过拟合。（Dropout可以减小模型的过拟合）
4：局部响应归一化层(LRN)：提高精度,LRN现在好像用得不多了，一般使用BN。
5：双GPU并行运行，提高训练速度。
下图就是AlexNet的网络构架，下面就其进行简要分析：

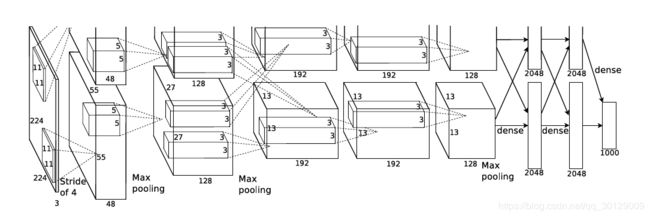
输入图像：在论文输入图像的大小是224224，但是在网上有人应该是227227.其实我认为两个都有其道理，假如说是224224的话，那么在第一层的卷积核中将padding设置为2即可，假如是227227的话，padding设置为0；
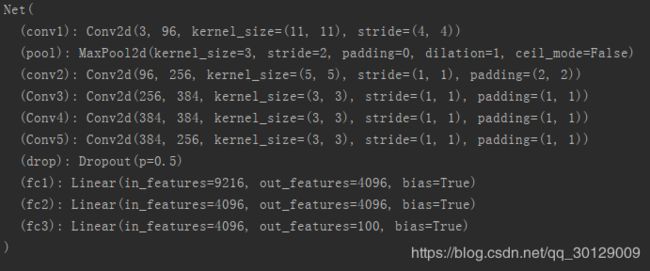
我用pytorch中的torchvision.model调用了AlexNet，然后将其网络架构输出，如下：

我发现torchvision.model中AlexNet的参数和论文中的参数是不一致的，所以我们还是就论文中的参数进行分析。

第一层：
卷积层：
torch.nn.Conv2d(3, 96, 11, 4, 0)输入图像是227×227×3，一共有96个11×11×3卷积核，生成96个feature map，步长为4，所以由$\frac{n-f+2p}{s}+1$（其中，n为输入图像的大小，f为卷积核大小，p为padding的大小，s为步长，并且向下取整）得到的Feature Map为55×55×96。又由于使用双GPU进行训练，所以分为两组，大小为55×55×48。

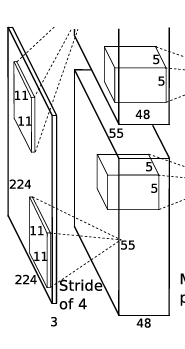
ReLU层：torch.nn.ReLU()然后又将输出的Feature Map经过RuLU层，增加网络中的非线性因素。
池化层+局部响应归一化：torch.nn.MaxPool2d(3,2)然后在经过池化层，使用的是3×3的步长为2的池化单元（这里是重叠池化，步长小于池化单元的大小）由$\frac{n-f}{s}+1$得到输出两组27×27×48的Feature Map。

第二层：
卷积层：
torch.nn.Conv2d(96, 256, 5, 1, 2)输入是两组27*27*48的Feature Map，这一层一共有256个5×5×3卷积核，生成256个feature map，步长为1，padding为2，所以由$\frac{n-f+2p}{s}+1$（其中，n为输入图像的大小，f为卷积核大小，p为padding的大小，s为步长），每组得到的Feature Map为27×27×128。

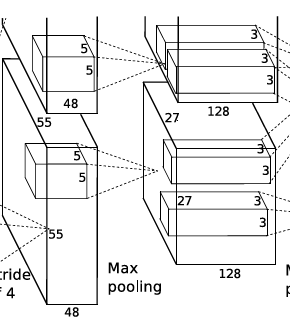
ReLU层：torch.nn.ReLU()然后又将输出的Feature Map经过RuLU层，增加网络中的非线性因素。
池化层+局部响应归一化：torch.nn.MaxPool2d(3,2)由卷积层二得到的Feature Map，将其经过池化层，使用3×3的步长为2的池化单元，由$\frac{n-f}{s}+1$得到每组的输出为13×13×128。

第三层：
卷积层：
torch.nn.Conv2d(256,384, 3, 1, 1)输入是两组13×13×128的Feature Map，这一层一共有384个3×3×3卷积核，生成384个feature map，步长为1，padding为1，所以由$\frac{n-f+2p}{s}+1$（其中，n为输入图像的大小，f为卷积核大小，p为padding的大小，s为步长），每组得到的Feature Map为13×13×384。

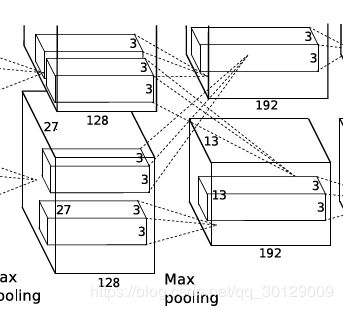
ReLU层：torch.nn.ReLU()然后又将卷积层输出的Feature Map经过RuLU层。输出是13×13×384，分为两组，每组为13×13×192.
第四层：
卷积层：
torch.nn.Conv2d(384,384, 3, 1, 1)输入是两组13×13×192的Feature Map，这一层一共有384个3×3×3卷积核，生成384个feature map，步长为1，padding为1，所以由$\frac{n-f+2p}{s}+1$（其中，n为输入图像的大小，f为卷积核大小，p为padding的大小，s为步长），每组得到的Feature Map为13×13×192。

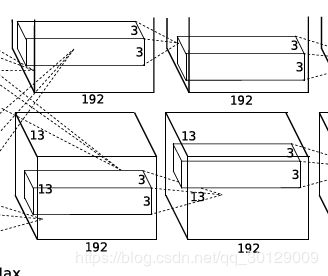
ReLU层：torch.nn.ReLU()然后又将卷积层输出的Feature Map经过RuLU层。输出是13×13×384，分为两组，每组为13×13×192.
第五层：
卷积层：
torch.nn.Conv2d(384,256, 3, 1, 1)输入是两组13*13*192的Feature Map，这一层一共有256个5×5×3卷积核，生成256个feature map，步长为1，padding为2，所以由$\frac{n-f+2p}{s}+1$（其中，n为输入图像的大小，f为卷积核大小，p为padding的大小，s为步长），每组得到的Feature Map为13×13×128。

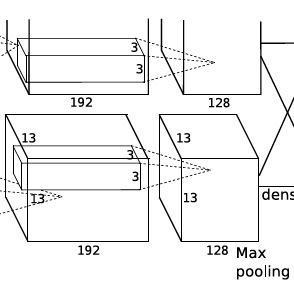
ReLU层：torch.nn.ReLU()然后又将输出的Feature Map经过RuLU层，增加网络中的非线性因素。
池化层+局部响应归一化：torch.nn.MaxPool2d(3,2)由卷积层二得到的Feature Map，将其经过池化层，使用3×3的步长为2的池化单元，由$\frac{n-f}{s}+1$得到每组的输出为6×6×128。总的输出为6×6×256

第六层：
全连接层：
这一层是卷积->全连接的连接：torch.nn.Linear(9216, 4096) 输入为6×6×256,该层有4096个卷积核，每个卷积核的大小为6×6×256。由于卷积核的尺寸刚好与待处理特征图（输入）的尺寸相同，即卷积核中的每个系数只与特征图（输入）尺寸的一个像素值相乘，一一对应，因此，该层被称为全连接层。由于卷积核与特征图的尺寸相同，卷积运算后只有一个值，因此，卷积后的像素层尺寸为4096×1×1，即有4096个神经元。

ReLU：这4096个运算结果通过ReLU激活函数生成4096个值
Dropout：torch.nn.Dropout(0.5)随机的断开断开50%神经元的连接，从而防止过拟合现象。

第七层：
全连接层：
这一层是全连接->全连接的连接：torch.nn.Linear(4096, 4096)

ReLU：这4096个运算结果通过ReLU激活函数生成4096个值
Dropout：torch.nn.Dropout(0.5)随机的断开50%神经元的连接，从而防止过拟合现象。

第八层：
输出层：第七层输出的4096个数据与第八层的1000个神经元进行全连接，输出一个元素个数为1000的一维向量。

pytorch实现：

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 96,11,4,0)  # 定义conv1函数的是图像卷积函数：输入为图像（3个频道，即彩色图）,输出为6张特征图, 卷积核为5x5正方形
        self.pool = nn.MaxPool2d(3, 2)
        self.conv2 = nn.Conv2d(96, 256, 5, 1, 2)
        self.Conv3 = nn.Conv2d(256, 384, 3, 1, 1)
        self.Conv4 = nn.Conv2d(384,384, 3, 1, 1)
        self.Conv5 = nn.Conv2d(384,256, 3, 1, 1)
        self.drop = nn.Dropout(0.5)
        self.fc1 = nn.Linear(9216, 4096)
        self.fc2 = nn.Linear(4096, 4096)
        self.fc3 = nn.Linear(4096, 100)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = F.relu(self.conv3(x))
        x = F.relu(self.conv4(x))
        x = self.pool(F.relu(self.conv5(x)))
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = self.drop(F.relu(self.fc1(x)))
        x = self.drop(F.relu(self.fc2(x)))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

明天继续修改一下细节。