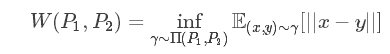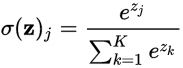论文中整理的零碎知识点

1.熵

信息熵:量化信息，小概率事件但信息量大比如月食，大概率事件信息量小比如太阳每天都从东方升起，所以采取在概率p前加一个log，再添负号，就满足前面的要求了，而这是针对单个个体，对-logp求期望Ex~p(-logp)是描述总体的信息量。

维基百科的解释：

在信息论中，熵（英语：entropy）是接收的每条消息中包含的信息的平均量，又被称为信息熵、信源熵、平均自信息量。这里，“消息”代表来自分布或数据流中的事件、样本或特征。（熵最好理解为不确定性的量度而不是确定性的量度，因为越随机的信源的熵越大。）来自信源的另一个特征是样本的概率分布。这里的想法是，比较不可能发生的事情，当它发生了，会提供更多的信息。由于一些其他的原因，把信息（熵）定义为概率分布的对数的相反数是有道理的。事件的概率分布和每个事件的信息量构成了一个随机变量，这个随机变量的均值（即期望）就是这个分布产生的信息量的平均值（即熵）。熵的单位通常为比特，但也用Sh、nat、Hart计量，取决于定义用到对数的底。

定义：

依据Boltzmann's H-theorem，香农把随机变量X的熵值 Η（希腊字母Eta）定义如下，其值域为{x1, ..., xn}：

。

其中，P为X的概率质量函数（probability mass function），E为期望函数，而I(X)是X的信息量（又称为自信息）。I(X)本身是个随机变数。

当取自有限的样本时，熵的公式可以表示为：

在这里b是对数所使用的底，通常是2,自然常数e，或是10。当b = 2，熵的单位是bit；当b = e，熵的单位是nat；而当b = 10,熵的单位是Hart。

pi = 0时，对于一些i值，对应的被加数0 logb 0的值将会是0，这与极限一致。

。

还可以定义事件 X 与 Y 分别取 xi 和 yj 时的条件熵为

其中p(xi, yj)为 X = xi 且 Y = yj 时的概率。这个量应当理解为你知道Y的值前提下随机变量 X 的随机性的量。

采用概率分布的对数作为信息的量度的原因是其可加性。例如，投掷一次硬币提供了1 Sh的信息，而掷m次就为m位。更一般地，你需要用log2(n)位来表示一个可以取n个值的变量

 

KL散度:衡量两个分布之间的距离，可以用来计算代价，不具备对称性。用这个q分布去逼近真实分布p，用logp-logq(logp-logq<0,原因暂且不知道)衡量逼近的程度，这也是针对一个个体，对logp-logq求期望Ex~p(logp)-Ex~p(logq)是总体的KL散度。

交叉熵:概率分布p与q之间的交叉熵是：用总体的信息熵加上总体的KL散度

离散分布p与q的交叉熵是：

在大多数情况下，我们需要在不知道分布{\displaystyle p}的情况下计算其交叉熵。例如在语言模型中, 我们基于训练集创建了一个语言模型, 而在测试集合上通过其交叉熵来评估该模型的准确率。是语料中词汇的真实分布，而是我们获得的语言模型预测的词汇分布。由于真实分布是未知的，我们不能直接计算交叉熵。在这种情况下，我们可以通过下式来估计交叉熵:

是测试集大小，是在训练集上估计的事件发生的概率。我们假设训练集是从的真实采样，则此方法获得的是真实交叉熵的蒙特卡洛估计。

JS散度：相似度衡量指标。现有两个分布P1和P2，其JS散度公式为：

 

 

Wasserstein距离度量两个概率分布之间的距离，定义如下：

2.凸函数

若这里凸集C即某个区间I，那么就是：设f为定义在区间I上的函数，若对I上的任意两点X1，X2和任意的实数λ∈（0，1），总有

 

f（λx1+(1-λ）x2）≤λf(x1)+(1-λ）f(x2),

 

则f称为I上的凸函数。损失函数只有是凸函数时，梯度下降法才能保证达到全局最优解。

凸集：实数 R （或复数 C 上）向量空间中，集合 S 称为凸集，如果 S 中任两点的连线内的点都在集合 S 内。

3.架构：

一旦产生的分工，就把所有的事情，切分成由不同角色的人来完成，最后再通过交易，使得每个个体都拥有生活必须品，而不需要每个个体做所有的事情，只需要每个个体做好自己擅长的事情，并具备一定的交易能力即可。这实际上就形成了社会的架构。

架构实际上就是指人们根据自己对世界的认识，为解决某个问题，主动地、有目的地去识别问题，并进行分解、合并，解决这个问题的实践活动

4.反向传播算法（Backpropagation）是目前用来训练人工神经网络（Artificial Neural Network，ANN）的最常用且最有效的算法。其主要思想是：

（1）将训练集数据输入到ANN的输入层，经过隐藏层，最后达到输出层并输出结果，这是ANN的前向传播过程；

（2）由于ANN的输出结果与实际结果有误差，则计算估计值与实际值之间的误差，并将该误差从输出层向隐藏层反向传播，直至传播到输入层；

（3）在反向传播的过程中，根据误差调整各种参数的值；不断迭代上述过程，直至收敛。

5.总变分(Total Variation)最小化方法

Rudin等人(Rudin1990)观察到，受噪声污染的图像的总变分比无噪图像的总变分明显的大。总变分定义为梯度幅值的积分：

 

JT0(u)=∫Ωu|▽u|dxdy=∫Duu2x+u2y−−−−−−√dxdy

 

其中ux=∂u∂x；uy=∂u∂y；Du是图像的支持域。限制总变分就会限制噪声。

6.The idea behind the GANs is very straightforward. Two networks -- a Generator and a Discriminator play a game against each other

 

7. trained classifier训练分类器    pixels像素   ill-condition病态  condition number状态数  well-condition良态   Mathematical notation数学符号  expect期待，预料 imperceptible感觉不到的  chaotic混沌的，无秩序的   Minimax theorem极小极大定理   Nash equilibrium纳什均衡   compelling令人叹服的

 

8.范数

L0范数是指向量中非0的元素的个数。

L1范数是指向量中各个元素绝对值之和。

既然L0可以实现稀疏，为什么不用L0，而要用L1呢？个人理解一是因为L0范数很难优化求解（NP难问题），二是L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解。所以大家才把目光和万千宠爱转于L1范数。

L2范数是指向量各元素的平方和然后求平方根

L2避免过拟合的原理是：让L2范数的规则项||W||2 尽可能小，可以使得W每个元素都很小，接近于零，但是与L1不同的是，不会等于0；这样得到的模型抗干扰能力强，参数很小时，即使样本数据x发生很大的变化，模型预测值y的变化也会很有限。

L2范数除了避免过拟合问题，还有一个优点是有助于处理condition number不好的情况下，矩阵求解困难的问题。

9.SGD:现在的SGD一般都指mini-batch gradient descent10.

 

10.先验概率：通过以往经验获得的概率

   后验概率：得到结果的信息，再回过头来修正先验概率。

11.生成器也可以叫解码器

解码器--把数字信号（离散型数值）还原成模拟信号（值是连续的）的软硬件设备

生成器--函数，可以生成连续的x值

12.感知机：一种分类方法，前提是数据线性可分。对于二维平面，找到一条直线将二元类别分隔；对于高维平面，找到一个超平面。泛化能力不强。

对于数据不可分，它的对手:

支持向量机：引入核函数让数据在高维可分

神经网络：增加隐藏层让数据可分

多层感知机(MLP)：也叫人工神经网络（ANN）。有输入层，隐藏层，输出层。

13.受限玻尔兹曼机->概率图模型->贝叶斯网络，马尔可夫网络，隐马尔可夫网络

概率图模型(PGM)：用图来表示变量概率依赖关系的理论，节点表示随机变量，边表示依赖关系

贝叶斯网络：http://www.dataguru.cn/thread-508373-1-1.html

先验分布 + 样本信息  后验分布         

条件概率：事件A在事件B发生之后发生的概率，表示为P(A|B)

联合概率：表示多个事件共同发生的概率。指在多元的概率分布中多个随机变量分别满足各自条件的概率

边缘概率：某个事件发生的概率边缘概率是这样得到的：在联合概率中，把最终结果中那些不需要的事件通过合并成它们的全概率，而消去它们（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率），这称为边缘化（marginalization），比如A的边缘概率表示为P(A)，B的边缘概率表示为P(B)。

贝叶斯公式：

 

马尔可夫性：下一时刻的状态只与上一时刻的状态有关，无后效性。

齐次马尔可夫性：一步转移概率与初始时刻无关。 

条件随机场(CRF)：:条件概率分布

随机场：当给每一个位置中按照某种分布随机赋予相空间的一个值之后，其全体就叫做随机场。

马尔可夫网络，（马尔可夫随机场、无向图模型）：http://blog.csdn.net/zhubo22/article/details/25100561是关于一组有马尔可夫性质随机变量的全联合概率分布模型。它指的是一个随机变量序列按时间先后关系依次排开的时候，第N+1时刻的分布特性，与N时刻以前的随机变量的取值无关。

隐马尔可夫网络：

受限的玻尔兹曼机：

14.优化算法：

梯度下降法：是一种最优化算法，原理是沿着梯度下降的方向来求出一个函数的极小值。

缺点：一是不能保证被优化函数达到全局最优，二是计算时间太长。

 

加速训练过程：随机梯度下降法SGD

最初只随机优化某条数据上的损失函数，存在的问题是在某条数据上损失函数更小并不代表在全部数据上损失函数更小，于是使用随机梯度下降算法得到的神经网络甚至不能达到局部最优。

 

现在的SGD一般都指mini-batch gradient descent10. 每次计算一小部分训练数据（叫一个batch）的损失函数

http://www.cnblogs.com/Sinte-Beuve/p/6164689.html

还有其他优化器https://blog.csdn.net/g11d111/article/details/76639460#

     梯度：  

       梯度是一个矢量，一个点的梯度方向就是该点方向导数（通过对该点的长度为1的任意方向求导）取得最大的方向，值为最大方向导数的值。

       若有一个二元函数z=f(x, y)，当它由点A移动到点B时（设移动的距离为L），此时函数值z有一个增量M。当L趋于无限小时，若M/L有一个极限值，那么这个极限值就叫做函数在方向AB上的方向导数。经过点函数可以朝任意方向移动（当然移动的范围必须在定义域内），函数就有任意多个方向导数，但其中有一个方向上方向导数肯定最大，这个方向就用梯度（grad=ai+bj）这个向量来表示，其中a是函数在x方向上的偏导数，b是函数在y方向上的偏导数，梯度的模就是这个最大方向导数的值。

 簇梯度：

   LBFGS: https://blog.csdn.net/qq_23052951/article/details/55274112

15.再生核希尔伯特空间：http://blog.csdn.net/susan_wang1/article/details/50470629

                   

 

16.核函数（径向基函数RBF）：某种沿着径向（指沿直径或半径的直线方向，或者与垂直于它们的直线方向）对称的标量函数。通常定义为空间中任一一点x到某一中心xc之间欧氏距离（坐标系中两点距离公式）的单调函数，作用往往是局部的，当x远离xc是函数取值很小。

 

17.复函数：复函数这个概念的核心应该是值域为C，至于定义域，一般是数集C，当然也可以拓展到向量，到欧式空间，到H,B空间

 

18.sup上确界：对于函数的每个取值，总能找到一个比你函数值都大的值，值是不唯一的，但有个最小值即为上确界。

 

19.无偏估计：估计量的数学期望等于被估计参数的真实值，则称此此估计量为被估计参数的无偏估计

 

20.闭包：函数a的内部函数b，被函数a外部的一个变量引用的时候，就创建了一个闭包。

 

21.？仅知道从p中获得独立同分布的样本，只能对进行经验评估

 

22.LDA( latent Dirichlet allocation )

  LDA is a generative statistical model that allows sets of observations to be explained by unobserved groups that explain why some parts of the data are similar.

 

23.激活函数

常用的激活函数总结(Sigmoid函数、Tanh函数、ReLu函数、Softmax函数)

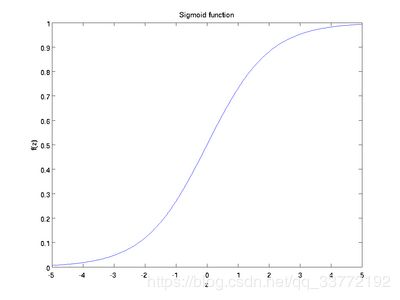
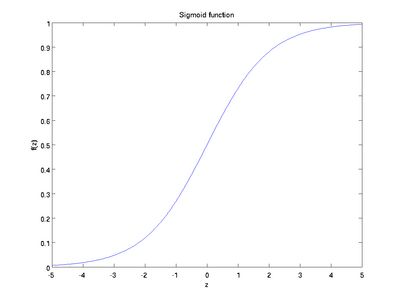
Sigmoid （LSTM中有用到）

也成为 S 形函数，取值范围为 (0,1)。Sigmoid 将一个实数映射到 (0,1) 的区间，可以用来做二分类。Sigmoid 在特征相差比较复杂或是相差不是特别大时效果比较好。

sigmoid 缺点：

• 激活函数计算量大（指数运算），反向传播求误差梯度时，求导涉及除法

• 对于深层网络，sigmoid 函数反向传播时，很容易就会出现梯度消失的情况（在 sigmoid 接近饱和区时，变换太缓慢，导数趋于 0，这种情况会造成信息丢失），从而无法完成深层网络的训练

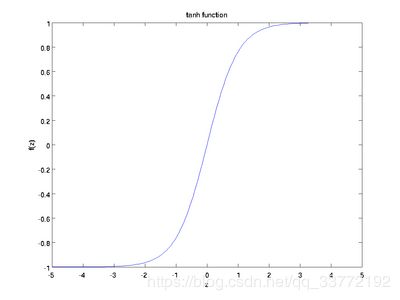
Tanh （全连接层中使用到）

也称为双切正切函数，取值范围为 [-1,1]。tanh 在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果。

Softmax （将向量的每个分量压缩到0-1直接的数）

softmax 函数将 K 维的实数向量压缩（映射）成另一个 K 维的实数向量，其中向量中的每个元素取值都介于 (0，1) 之间。常用于多分类问题。

Softmax is a generalization of the logistic function that "squashes" a K-dimensional vector z of arbitrary real values to a K-dimensional vector sigma(z) of real values in the range (0, 1) that add up to 1.

ReLU （在神经网络的前向传播过程的结果有用到）

为什么采用 ReLU：

• sigmoid 等激活函数（指数运算）计算量大，并且在深层网络上容易出现梯度消失问题

• ReLU 计算量小（不涉及除法），一部分神经元的输出为 0 造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生

对于偏置值，如果用 ReLU 的话，最好的办法就是把它们都初始化成小的正值，这样神经元一开始就会工作在 ReLU 的非零区域内。

ReLU 缺点：强制的稀疏处理会减少模型的有效容量（即特征屏蔽太多，导致模型无法学习到有效特征）。

 

24.exposure bias

训练的时候，每个时刻的输入都是来自于真实的caption。而生成的时候，每个时刻的输入来自于前一时刻的输出；所以一旦有一个单词生成的不好，错误可能会接着传递，使得生成的越来越糟糕。

论文SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient中有提到。

 

25.one-hot vector

一位有效位编码，主要指机器学习中某些特征不是连续值，性别["male","female"]，地区["Europe","US" ,"Asia"], 览器：["Firefox"，"Chrome"，"Safari"，"Internet Explorer"], 这样，我们可以采用One-Hot编码的方式对上述的样本“["male"，"US"，"Internet Explorer"]”编码，“male”则对应着[1，0]，同理“US”对应着[0，1，0]，“Internet Explorer”对应着[0,0,0,1]。则完整的特征数字化的结果为：[1,0,0,1,0,0,0,0,1]。这样导致的一个结果就是数据会变得非常的稀疏。

 

26.baselines: 实验结果的第一部分就是重复前人最成功的实验（一般被称为基准，Baseline）

 

27.prior：看具体情况，有时候指先验分布，有时候指先验概率。

 

28.BatchSize: Batch 的选择，首先决定的是下降的方向

                            过大占内存，过小很难收敛 https://blog.csdn.net/ycheng_sjtu/article/details/49804041

                            https://blog.csdn.net/tsq292978891/article/details/78619384

                             Full Batch Learning，全数据集，

                             batch_size=1在线学习

                             批梯度下降法（Mini-batches Learning）：适中的batch_size,因为如果数据集足够充分，那么用一半（甚至少得多）的数据训练算出来的梯度与用全部数据训练出来的梯度是    几乎一样的。

 

29.数据噪声： 数据噪声指在一组数据中无法解释的数据变动，就是一些不和其他数据相一致的数据。 噪声（noise）是被测量的变量的随机误差或方差。

                        

 链接：https://www.zhihu.com/question/53316946/answer/134515831

1、为什么受噪声影响，任何一种模型的复杂度就随之增加嘛？

首先咱们回答第1个问题，这个问题很简单，可以看下面第三幅图：

<img src="https://pic1.zhimg.com/50/v2-bcd970af7fd1d21420a95adf72fa0900_hd.jpg" data-rawwidth="600" data-rawheight="170" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic1.zhimg.com/v2-bcd970af7fd1d21420a95adf72fa0900_r.jpg">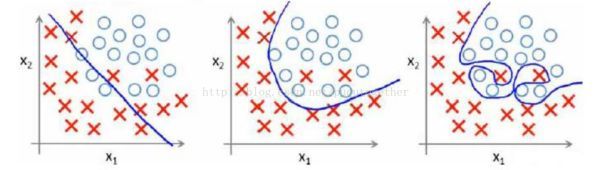

显然，最右边的一幅图是【过拟合】的状态，它产生的原因是在分类的过程当中有两个样本数据存在噪音，我们可以这样去理解这两个样本，他们的大部分特征都表示他们属于类别O，但是有两个样本存在特征偏差使得我们误分类为了X，或者可以说他的某些特征跟O一样，但是我们细分、深究之后得出这两个样本的分类实际上是X。可以用二分类{男人，女人}的例子，然后X代表男人，O代表女人，样本数据中出现了两个人妖。

所以呢，为了能够区分出某些个特征不是特别明显的样本，我们需要样本给我们提供更多的特征。特征的增加，导致了我们用f(x)模型去判别y的时候，多项式的项增加了，所以模型的复杂度增加了。其实冲上面的最右边那副图我们也可以看出，假设样本只有两个属性,我们要生成一个模型f(x)去区分类别{X，O}，显然有噪音影响的时候蓝色的线，即模型f(x),更加的复杂。

ps：相应的第二幅图中我们为了让模型更简单，有意识的去忽略了某些个特别离奇的样本（即人妖），这就是容错，第二幅图就是正则化后的图像。

所以第一个问题解答的很清楚了，噪音样本的增加肯定会导致模型的复杂度提高，因为我们为了拟合所有的样本需要的多项式的项数越多。

 

30.正则化：https://blog.csdn.net/wsj998689aa/article/details/39547771

                防止过拟合；

                约束（限制）要优化的参数。

 

31.seed 

rand()函数是根据seed值得到一个伪随机序列，如果seed相同，则得到的随机序列是相同的。

可以手动设置seed，需要通过函数srand(seed)实现。 设置好seed后，就会得到一个新的随机序列（一组数，不是一个数，可以连续运行rand()函数，得到这个序列中的各个数据）

一般我们用 srand(time(NULL)) 来保证程序在不同的时间点运行，可以得到不同的随机序列。

time(NULL) 函数是得到一个时间整数，以秒为单位。不同的时间点，其值不同。

 

32.损失函数

分类一般用softmax和cross entropy, 回归一般用均方误差

33.model collapse

                

Model collapse：给定一个z，当z发生变化的时候，对应的G(z)没有变化，那么在这个局部， GAN就发生里mode collapse, 也就是不能产生不断连续变化的样本。也就是生成的样本单一。

这个现象从几何上来看，就是对应的流型在这个局部点处，沿着不同的切向量方向不再有变化。换言之，所有切向量不再彼此相互独立--某些切向量要么消失，要么相互之间变得线性相关，从而导致流型的维度在局部出现缺陷（dimension deficient）。

 

 

怎么解决模式崩溃：可以给流型的切向量加上一个正交约束(Orthonormal constraint)，从而避免这种局部的维度缺陷。

34.baseline

前人做成功的实验叫做基准，一般的效果的实验叫baseline，特别好的那些叫benchmark。

 

35.exposure bias：看到了一篇论文https://arxiv.org/abs/1609.05473，它说极大似然方法在推断阶段会遭遇到exposure bias的问题，文章是这么说的：生成模型迭代的生成一个序列(句子），而预测下一个词是基于前一个预测的词（在训练阶段中可能没有见过），这种训练阶段和推断阶段的差异会累加，当序列长度变长时，差异更突出。引用的是Bengio《Scheduled sampling for sequence prediction with recurrent neural networks》https://arxiv.org/pdf/1506.03099.pdf这篇文章提出来的观点。

也就是训练的时候用真实数据训练，但预测的时候，每个词的预测都是基于前一个词，若前一个词从未见过，这会导致预测和训练产生差异，这种差异会产生错误。若当前词也是没见过的词，那么接下来预测的词又会基于这个没见过的词进行预测，这种错误会伴随序列累加，而且随着序列变长变得更突出。

 

36.自回归模型（AR)

自回归模型（英语：Autoregressive model，简称AR模型），是统计上一种处理时间序列的方法，用同一变数例如{\displaystyle x}的之前各期，亦即{\displaystyle x_{1}}至{\displaystyle x_{t-1}}来预测本期{\displaystyle x_{t}}的表现，并假设它们为一线性关系。因为这是从回归分析中的线性回归发展而来，只是不用{\displaystyle x}预测{\displaystyle y}，而是用{\displaystyle x}预测{\displaystyle x}（自己）；所以叫做自回归。

37.图灵测试

图灵测试（The Turing test）由艾伦·麦席森·图灵发明，指测试者与被测试者（一个人和一台机器）隔开的情况下，通过一些装置（如键盘）向被测试者随意提问。

进行多次测试后，如果有超过30%的测试者不能确定出被测试者是人还是机器，那么这台机器就通过了测试，并被认为具有人类智能。图灵测试一词来源于计算机科学和密码学的先驱阿兰·麦席森·图灵写于1950年的一篇论文《计算机器与智能》，其中30%是图灵对2000年时的机器思考能力的一个预测，目前我们已远远落后于这个预测。 

38.退化问题（degradation problem）

随着网络深度的增加，训练的准确率达到饱和，开始迅速退化。

解决方法：构造更深的网络：添加实体映射的层，其他层直接拷贝已学过的比较浅的层。

http://openaccess.thecvf.com/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf

 

39.FLOPs

以下解释来自知乎，链接：https://www.zhihu.com/question/65305385/answer/451060549

 

FLOPs：FLOPS：注意全大写，是floating point operations per second的缩写，意指每秒浮点运算次数，理解为计算速度。是一个衡量硬件性能的指标。

FLOPs：注意s小写，是floating point operations的缩写（s表复数），意指浮点运算数，理解为计算量。可以用来衡量算法/模型的复杂度。

 

网上打字很容易全小写，造成混淆，本问题针对模型，应指的是FLOPs。

以下答案不考虑activation function的运算。

 

卷积层：

Ci=input channel, k=kernel size, HW=output feature map size, Co=output channel.

2是因为一个MAC算2个operations。

不考虑bias时有-1，有bias时没有-1。

上面针对一个input feature map，没考虑batch size。

理解上面这个公式分两步，括号内是第一步，计算出output feature map的一个pixel，然后再乘以HWCo拓展到整个output feature map。括号内的部分又可以分为两步， ，第一项是乘法运算数，第二项是加法运算数，因为n个数相加，要加n-1次，所以不考虑bias，会有一个-1，如果考虑bias，刚好中和掉，括号内变为

 

全联接层：

I=input neuron numbers, O=output neuron numbers.

2是因为一个MAC算2个operations。

不考虑bias时有-1，有bias时没有-1。

分析同理，括号内是一个输出神经元的计算量，拓展到O了输出神经元。

 

还有一篇文章叫《attention is all you need》https://papers.nips.cc/paper/7181-attention-is-all-you-need.pdf有计算模型的训练成本的方法，里面有详细的计算方法非常可行，跟上面略有不同。

 

40.极大似然估计

知乎：https://zhuanlan.zhihu.com/p/26614750

极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！

换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

41.过拟合

在统计学中，过拟合（英语：overfitting，或称过度拟合）现象是指在拟合一个统计模型时，使用过多参数。

对比于可获取的数据总量来说，一个荒谬的模型只要足够复杂，是可以完美地适应数据。过拟合一般可以视为违反奥卡姆剃刀原则。

当可选择的参数的自由度超过数据所包含信息内容时，这会导致最后（拟合后）模型使用任意的参数，这会减少或破坏模型一般化的能力更甚于适应数据。过拟合的可能性不只取决于参数个数和数据，也跟模型架构与数据的一致性有关。此外对比于数据中预期的噪声或错误数量，跟模型错误的数量也有关。