五大常用算法之一：贪心算法

贪心算法

贪婪算法(贪心算法)是指在对问题进行求解时，在每一步选择中都采取最好或者最优(即最有利)的选择，从而希望能够导致结果是最好或者最优的算法。
贪心算法每一步必须满足一下条件：

1. 可行的：即它必须满足问题的约束。
2. 局部最优：他是当前步骤中所有可行选择中最佳的局部选择。
3. 不可取消：即选择一旦做出，在算法的后面步骤就不可改变了。

基本思路：

1. 建立数学模型来描述问题
2. 把求解的问题分成若干个子问题
3. 对每一子问题求解，得到子问题的局部最优解
4. 把子问题对应的局部最优解合成原来整个问题的一个近似最优解

贪心算法案例：

1.活动选择问题：

这是《算法导论》上的例子，也是一个非常经典的问题。有n个需要在同一天使用同一个教室的活动a1,a2,…,an，教室同一时刻只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi 。一旦被选择后，活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠，ai和aj两个活动就可以被安排在这一天。该问题就是要安排这些活动使得尽量多的活动能不冲突的举行。例如下图所示的活动集合S，其中各项活动按照结束时间单调递增排序。

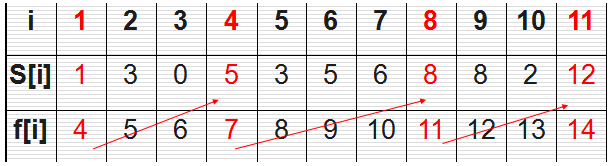
用贪心法的话思想很简单：活动越早结束，剩余的时间是不是越多？那我就早最早结束的那个活动，找到后在剩下的活动中再找最早结束的不就得了？

虽然贪心算法的思想简单，但是贪心法不保证能得到问题的最优解，如果得不到最优解，那就不是我们想要的东西了，所以我们现在要证明的是在这个问题中，用贪心法能得到最优解。

java代码实现

public class ActiveTime {
    public static void main(String[] args) {
        //创建活动并添加到集合中
        Active act1 = new Active(1, 4);
        Active act2 = new Active(3, 5);
        Active act3 = new Active(0, 6);
        Active act4 = new Active(5, 7);
        Active act5 = new Active(3, 8);
        Active act6 = new Active(5, 9);
        Active act7 = new Active(6, 10);
        Active act8 = new Active(8, 11);
        Active act9 = new Active(8, 12);
        Active act10 = new Active(2, 13);
        Active act11 = new Active(12, 14);
        List actives = new ArrayList();
        actives.add(act1);
        actives.add(act2);
        actives.add(act3);
        actives.add(act4);
        actives.add(act5);
        actives.add(act6);
        actives.add(act7);
        actives.add(act8);
        actives.add(act9);
        actives.add(act10);
        actives.add(act11);
        
        List bestActives  = getBestActives(actives, 0, 16);
        for (int i = 0; i < bestActives.size(); i++) {
            System.out.println(bestActives.get(i));
        }
    }


    /**
     * 
     * @param actives
     *            活动集合
     * @param startTime
     *            教室的开始使用时间
     * @param endTime
     *            教室的结束使用时间
     * @return
     */
    public static List getBestActives(List actives, int startTime, int endTime) {
        //最佳活动选择集合
        List bestActives = new ArrayList();
        //将活动按照最早结束时间排序
        actives.sort(null);
        //nowTime 用来记录上次活动结束时间
        int nowTime = startTime;
        /**
         * 因为我们已经按照最早结束时间排序，那么只要活动在时间范围内
         * actives.get(1)就应当是第一个活动的结束时间.
         * 则我们记录第一次活动结束的时间，在结合剩下的活动中，
         * 选取开始时间大于nowTime且结束时间又在范围内的活动，则为第二次活动时间，
         * 知道选出所有活动
         */
        for (int i = 0; i < actives.size(); i++) {
            Active act = actives.get(i);
            if(act.getStartTime()>=nowTime&&act.getEndTime()<=endTime){
                bestActives.add(act);
                nowTime = act.getEndTime();
            }
        }
        return bestActives;
    }
}

/**
 * 活动类
 * @CreatTime 下午9:45:37
 *
 */
class Active implements Comparable{
    private int startTime;//活动开始时间
    private int endTime;//活动结束时间

    public Active(int startTime, int endTime) {
        super();
        this.startTime = startTime;
        this.endTime = endTime;
    }

    public int getStartTime() {
        return startTime;
    }

    public void setStartTime(int startTime) {
        this.startTime = startTime;
    }

    public int getEndTime() {
        return endTime;
    }

    public void setEndTime(int endTime) {
        this.endTime = endTime;
    }
    
    @Override
    public String toString() {
        return "Active [startTime=" + startTime + ", endTime=" + endTime + "]";
    }
    
    //活动排序时按照结束时间升序
    @Override
    public int compareTo(Active o) {
        if(this.endTime>o.getEndTime()){
            return 1;
        }else if(this.endTime == o.endTime){
            return 0;
        }else{
            return -1;
        }
    }


}

运行结果：

Active [startTime=1, endTime=4]
Active [startTime=5, endTime=7]
Active [startTime=8, endTime=11]
Active [startTime=12, endTime=14]

可以看出，求得的结果正好是最优解。

2.钱币找零问题：

这个问题在我们的日常生活中就更加普遍了。假设1元、2元、5元、10元、20元、50元、100元的纸币分别有c0, c1, c2, c3, c4, c5, c6张。现在要用这些钱来支付K元，至少要用多少张纸币？用贪心算法的思想，很显然，每一步尽可能用面值大的纸币即可。在日常生活中我们自然而然也是这么做的。在程序中已经事先将Value按照从小到大的顺序排好。

java代码实现：

package GreedyAlgorithm;

public class CoinChange {
    public static void main(String[] args) {
        //人民币面值集合
        int[] values = { 1, 2, 5, 10, 20, 50, 100 };
        //各种面值对应数量集合
        int[] counts = { 3, 1, 2, 1, 1, 3, 5 };
        //求442元人民币需各种面值多少张
        int[] num = change(442, values, counts);
        print(num, values);
    }

    public static int[] change(int money, int[] values, int[] counts) {
        //用来记录需要的各种面值张数
        int[] result = new int[values.length];

        for (int i = values.length - 1; i >= 0; i--) {
            int num = 0;
            //需要最大面值人民币张数
            int c = min(money / values[i], counts[i]);
            //剩下钱数
            money = money - c * values[i];
            //将需要最大面值人民币张数存入数组
            num += c;
            result[i] = num;
        }
        return result;
    }

    /**
     * 返回最小值
     */
    private static int min(int i, int j) {
        return i > j ? j : i;
    }
    
    private static void print(int[] num, int[] values) {
        for (int i = 0; i < values.length; i++) {
            if (num[i] != 0) {
                System.out.println("需要面额为" + values[i] + "的人民币" + num[i] + "张");
            }
        }
    }
}

运行结果：

需要面额为2的人民币1张
需要面额为5的人民币2张
需要面额为10的人民币1张
需要面额为20的人民币1张
需要面额为100的人民币4张

可以看出，求出的结果也刚好等于442元。正好为最优解。但是，当面额及数量为下种特殊情况时，贪心算法就无法给出最优解。

//人民币面值集合
6 int[] values = { 3, 5, 10, 20, 50, 100 };
7 //各种面值对应数量集合
8 int[] counts = { 3, 2, 1, 1, 3, 5 };
需要求得money = 416元
运行结果如下：

需要面额为5的人民币1张
需要面额为10的人民币1张
需要面额为100的人民币4张

于是我们可以看出，有些情况，贪心算法确实可以给出最优解，然而，还有一些问题并不是这种情况。对于这种情况，我们关心的是近似解，或者只能满足于近似解，贪心算法也是有价值的。

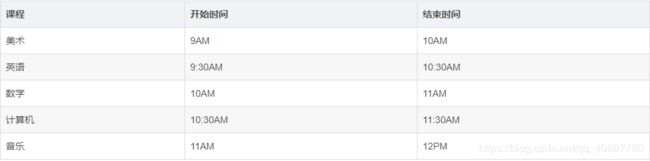
3.区间调度问题:

假设有如下课程，希望尽可能多的将课程安排在一间教室里：

这个问题看似要思考很多，实际上算法很简单:

1.选择结束最早的课，便是要在这教室上课的第一节课 2.接下来，选择第一堂课结束后才开始的课，并且结束最早的课，这将是第二节在教室上的课。

重复这样做就能找出答案，这边的选择策略便是结束最早且和上一节课不冲突的课进行排序，因为每次都选择结束最早的，所以留给后面的时间也就越多，自然就能排下越多的课了。

每一节课的选择都是策略内的局部最优解(留给后面的时间最多)，所以最终的结果也是近似最优解(这个案例上就是最优解)。 (该案例的代码实现，就是一个简单的时间遍历比较过程