我的算法笔记
算法分类
- 设计类
- LFU缓存
- LRU缓存
- Hashmap
- 排序算法类
- 背包问题类
- hashmap类
- 2数3数4数之和
- DFS和BFS
- BFS
- 动态规划
- ip地址类
- 栈/队列
- 二叉树
- 链表
- 字符串
- 位运算
- 二分查找
- 排列组合问题
- 回溯法
- 正则表达式匹配【分类讨论思想】
- java算法api
- hashmap巧解题
- 位运算
- &,|,~,^,>>,<<,>>>
设计类
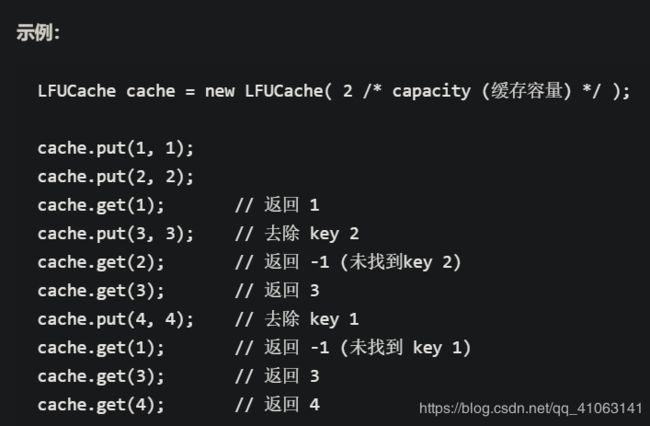
LFU缓存
class LFUCache {
Map<Integer, Node> cache; // 存储缓存的内容(key,node)
Map<Integer, LinkedHashSet<Node>> freqMap; // 存储每个频次对应的双向链表(同频次的可能有多个,所以需要用链表结构表示)
int size;
int capacity;
int min; // 存储当前最小频次
public LFUCache(int capacity) {
cache = new HashMap<> (capacity);
freqMap = new HashMap<>();
this.capacity = capacity;
}
public int get(int key) {
Node node = cache.get(key);
if (node == null) {
return -1;
}
freqInc(node);
return node.value;
}
public void put(int key, int value) {
if (capacity == 0) {
return;
}
Node node = cache.get(key);
if (node != null) {
node.value = value;
freqInc(node);
} else {
if (size == capacity) {
Node deadNode = removeNode();
cache.remove(deadNode.key);
size--;
}
Node newNode = new Node(key, value);
cache.put(key, newNode);
addNode(newNode);
size++;
}
}
void freqInc(Node node) {
// 从原freq对应的链表里移除, 并更新min
int freq = node.freq;
LinkedHashSet<Node> set = freqMap.get(freq);
set.remove(node);
if (freq == min && set.size() == 0) {
min = freq + 1;
}
// 加入新freq对应的链表
node.freq++;
LinkedHashSet<Node> newSet = freqMap.get(freq + 1);
if (newSet == null) {
newSet = new LinkedHashSet<>();
freqMap.put(freq + 1, newSet);
}
newSet.add(node);
}
void addNode(Node node) {
LinkedHashSet<Node> set = freqMap.get(1);
if (set == null) {
set = new LinkedHashSet<>();
freqMap.put(1, set);
}
set.add(node);
min = 1;
}
Node removeNode() {
LinkedHashSet<Node> set = freqMap.get(min);
Node deadNode = set.iterator().next();
set.remove(deadNode);
return deadNode;
}
}
class Node {
int key;
int value;
int freq = 1;
public Node() {}
public Node(int key, int value) {
this.key = key;
this.value = value;
}
}
LRU缓存
public class LRUCache{
int capacity;
Map<Integer, Integer> map;
public LRUCache(int capacity) {
this.capacity = capacity;
map = new LinkedHashMap<>();
}
public int get(int key) {
if (!map.containsKey(key)) {
return -1;
}
//先删除旧的位置,再放入新位置
Integer value = map.remove(key);
map.put(key, value);
return value;
}
public void put(int key, int value) {
if (map.containsKey(key)) {
map.remove(key);
map.put(key, value);
return;
}
map.put(key, value);
//超出capacity,删除最久没用的,利用迭代器,删除第一个
if (map.size() > capacity) {
map.remove(map.entrySet().iterator().next().getKey());
}
}
}
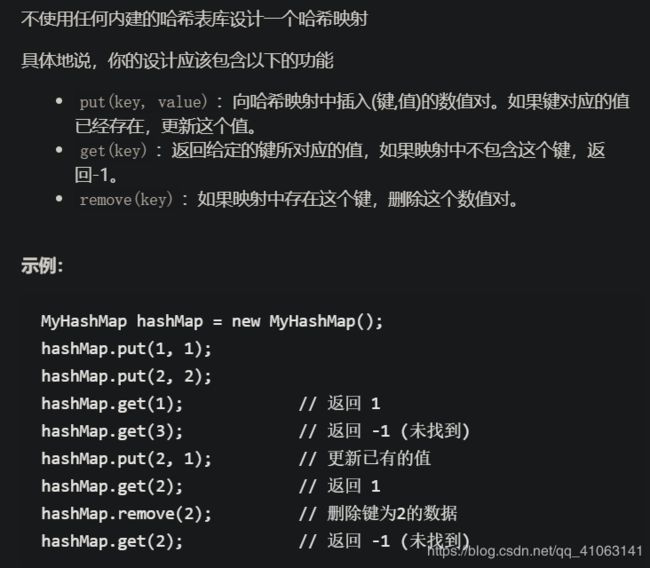
Hashmap
排序算法类
归并/堆排/快排
背包问题类
背包问题
hashmap类
使用时有一个前提:返回的结果都在数组里面。因为返回的是两个数,所以list.add()要添加两次。
array和map联合使用,取长补短.map中存入Array[i]作为键,将对应的下标作为值
| Array[i] | i |
|---|---|
| K | V |
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/two-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
List<Integer> result=new ArrayList<>();
Map<Integer,Integer>map=new HashMap<>();
public int[] twoSum(int[] nums, int target) {
for(int i=0;i<nums.length;i++){
if(map.containsKey(target-nums[i])){
result.add(i);
result.add(map.get(target-nums[i]));
}else{
map.put(nums[i],i);
}
}
return result.stream().mapToInt(Integer::intValue).toArray();
}
}
2数3数4数之和
DFS和BFS
BFS
BFS【解最短路径类问题】
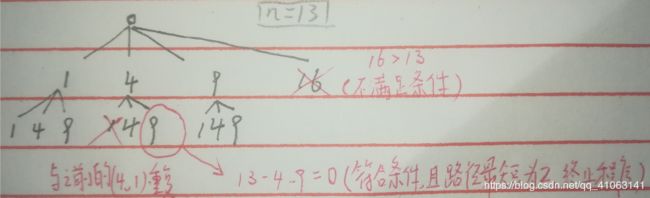
完 全 平 方 数 \color{red}{完全平方数} 完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n,你需要让组成和的完全平方数的个数最少
public int numSquares(int n) {
//1. 初始化三元素
//队列:先入先出的容器;
Queue<Integer> queue=new LinkedList<>();
//已访问集合:为了避免队列中插入重复的值
HashSet<Integer> visited=new HashSet<>(); //【创建 set 来存放非重复的元素】
//节点:最好写成单独的类,比如本例写成 (value,step) 元组。也可写成 (value,visited),看自己喜好和题目;
int count=0; //【定义 count 记录完全平方数的个数】
queue.offer(n); //在容量已满的情况下,add() 方法会抛出IllegalStateException异常,offer() 方法只会返回 false
visited.add(n);
while(!queue.isEmpty()){
count++; // 【每次有元素入队就代表还有剩余子平方数】
int len=queue.size(); //当层次遍历第二层是先记录下第一层的个数3【先固定下来】
for(int i=0;i<len;i++){ //不能写成i
//2. 操作队列 —— 弹出队首节点:
int curNode=queue.poll();//【1{1,4,9},4{1,4,9},9{1,4,9}】外层的1,4,9是在队列里面的。该层循环不能省略
//3. 操作弹出的节点 —— 根据业务生成子节点(一个或多个):
for(int j=1;j*j<=curNode;j++){ // 【从 1 开始取,每次拿平方数来比较】
int nextNode=curNode-j*j; // 【用当前结点减去平方数 1,4,9...】
//4. 判断这些节点 —— 符合业务条件,则return,
if(nextNode==0) // 【找完所有的平方数即可返回】
return count;
//不符合业务条件,且不在已访问集合,则追加到队尾,并加入已访问集合:
if(!visited.contains(nextNode)) { // 【如果 set 里面没有存放当前元素,则可以入队,入 set】
queue.offer(nextNode);
visited.add(nextNode);
}
}
}
}
//5. 若以上遍历完成仍未return,那就返回未找到代码(0):
return 0;
}
闯 迷 宫 \color{red}{闯迷宫} 闯迷宫
在一个nn的矩阵里走,从原点(0,0)开始走到终点(n-1,n-1),只能上下左右4个方向走,只能在给定的矩阵里走,求最短步数。nn是01矩阵,0代表该格子没有障碍,为1表示有障碍物。
int mazeArr[maxn][maxn]; //表示的是01矩阵
int stepArr[4][2] = {{-1,0},{1,0},{0,-1},{0,1}}; //表示上下左右4个方向
int visit[maxn][maxn]; //表示该点是否被访问过,防止回溯,回溯很耗时。
public class Test {
public static void main(String[] args) {
System.out.println(bfs(4));
}
static int mazeArr[][] = new int[][]{{0, 0, 1, 0}, {0, 0, 1, 0}, {0, 0, 0, 0}, {1, 0, 0, 0}}; //表示的是01矩阵(4,4)
static int[][] stepArr = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; //表示左右上下4个方向 ,(4,2)的二维数组【一个节点左右上下都尝试走一遍后将其加入到队尾,再从队列弹出下一个节点】
static int[][] visit = new int[4][4]; //表示该点是否被访问过,防止回溯,回溯很耗时。
private static int bfs(int n) {
Node node = new Node(0, 0, 0);
Queue<Node> queue = new LinkedList<Node>();
queue.add(node);
while (!queue.isEmpty()) {
Node newNode = queue.poll();
visit[newNode.x][newNode.y] = 1;
for (int i = 0; i < 4; i++) {
int x = newNode.x + stepArr[i][0];
int y = newNode.y + stepArr[i][1];
if (x == n - 1 && y == n - 1) {
return newNode.step + 1;
}
if (x >= 0 && y >= 0 && x < n && y < n
&& visit[x][y] == 0 && mazeArr[x][y] == 0) {
Node next = new Node(x, y, newNode.step + 1);
queue.add(next);
}
}
}
return -1;
}
private static class Node {
private int x;
private int y;
private int step;
public Node(int x, int y, int step) {
super();
this.x = x;
this.y = y;
this.step = step;
}
}
}
动态规划
动态规划
ip地址类
复制ip地址–回溯法
验证ip地址–分治法
栈/队列
双端队列和普通队列最大的不同在于,它允许我们在队列的头尾两端都能在 O(1)O(1) 的时间内进行数据的查看、添加和删除。
与队列相似,我们可以利用一个双链表实现双端队列。双端队列最常用的地方就是实现一个长度动态变化的窗口或者连续区间,而动态窗口这种数据结构在很多题目里都有运用。
作者:LeetCode
链接:https://leetcode-cn.com/problems/sliding-window-maximum/solution/hua-dong-chuang-kou-zui-da-zhi-by-leetcode-3/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
针对力扣官方视频的题解笔记如下:
蓝色区域维护的是一个双端单调(递减)队列。首先1入队,然后3入队,由于1<3违背了单调递减,所以移除队列里的1,接着-1入队,此时滑动窗口内的元素达到了k,标记当前串口最大值所在的下标(或者直接输出队首元素也行),接着5入队,依照递减,需要移除3,-1,-3。
双端队列(单调双关队列)
视频详解
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
if(n == 0) return nums;
int[] res = new int[n - k + 1];
//dq里面存的是数组的index, 不是数组的值
//这个dq队列才是滑动窗口
Deque<Integer> dq = new LinkedList<>();
for(int i = 0; i < n; i++){
//Step1: 头: 移除头部, 保证窗口的长度范围
//如果没有后一个判断,可能dp长度会为4,不符合规定的3
if(!dq.isEmpty() && dq.getFirst() < (i - k + 1)){
dq.removeFirst();//poll();
}
//Step2: 尾: 移除尾部小于当前值得元素, 原理参考篮球队长模型, 去除不可能的元素
while(!dq.isEmpty() && nums[i] >= nums[dq.getLast()]){
dq.removeLast();
}
//Step3: 尾部加入, 滑动窗口向右扩充
dq.addLast(i);
//Step4: 头, 从头部返回极大值
if(i >= k - 1){
res[i - k + 1] = nums[dq.getFirst()];
}
}
return res;
}
}
二叉树
二叉树的前中后序遍历—非递归实现
二叉树的前中后序遍历—递归实现
链表
反 转 单 链 表 \color{red}{反转单链表} 反转单链表
public static ListNode reverseLinkedList(ListNode header) {
if (header == null || header.next == null) return header;
ListNode p = null;
ListNode c=header;
ListNode n =header.next;
while (n != null) {
c.next=p;
p=c;
c=n;
n=n.next;
}
c.next=p;
return c;
}
字符串
位运算
输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
public class Solution {
public static void main(String[] args) {
int a=new Solution().NumberOf1(2);
System.out.println(a);
}
public int NumberOf1(int n) {
int count=0;
while(n!=0){
n=n&(n-1);
count++;
}
return count;
}
}
二分查找
public int search(int[] nums, int target) {
//注意点3---数组nums需要是有序的
int left = 0;
int right = nums.length - 1;
int mid = 0;
while (left <= right) { //注意点1
mid = (left + right) >>> 1; //注意点2
if (target == nums[mid]) return mid;
if (target < nums[mid]) right = mid - 1;
else left = mid + 1;
}
return -1;
}
class Solution {
public int splitArray(int[] nums,int m){
int n=nums.length;
int max=0;
int sum=0;
for (int num:nums) {
max=Math.max(max,num);
sum+=num;
}
int lo=max;
int hi=sum;
while (lo<hi){
int mid=(lo+hi)>>>1;
int pieces=split(nums,mid);
if (pieces>m){
lo=mid+1;
}else {
hi=mid;
}
}
return lo;
}
private int split(int[] nums, int largestSum) {
int pieces=1;
int tmpSum=0;
for (int num:nums){
if (tmpSum+num>largestSum){
tmpSum=num;
pieces++;
}else {
tmpSum+=num;
}
}
return pieces;
}
}
排列组合问题
- 比如给你数组[1,2,3],输出该数组所有可能的全排列
public class Solution {
boolean[] isused=new boolean[100];
List<Integer>templist=new ArrayList<>();
List<List<Integer>>rst=new ArrayList<>();
public static void main(String[] args) {
int[] a=new int[]{1,2,3};
List<List<Integer>> an=new Solution().arrange(a,0);
System.out.println(an);
}
public List<List<Integer>> arrange(int[] nums,int index) {
if (index==nums.length) {rst.add(new ArrayList<>(templist));}
// //这里会遍历nums.length*nums.length次
for (int i = 0; i <nums.length ; i++) {
if(!isused[i]){
isused[i]=true;
templist.add(nums[i]);
arrange(nums,index+1);
templist.remove(templist.size()-1);
isused[i]=false;
}
}
return rst;
}
}
对12345进行全排列
0{
0[
1,{0~4},2,{0~4},3,{4},4
]
1[
0{0~4},1,2,{0~4},2,{0~4},3,{0~4},4{0~4}
]
2[
0,{0~4},1,{0~4}.......
]
}
解释说明: 01{0~4}对应012,013,014即【123,124,125】
02{0~4}对应【132,134,135】
03{4}对应【145】
- 组合
/**
* 从1,2,3,4,5中选择3个数,求所有的组合
*/
public class Combination {
static List<List<Integer>>res=new ArrayList<>();
static List<Integer>list=new ArrayList<Integer>();
public static void main(String[] args) {
Combination combination = new Combination();
combination.combination(new int[]{1,2,3,4,5},3,0);
System.out.println(res);
System.out.println(res.size());
}
/**
* 在下一次循环开始之前,直接跳过下次循环,然后回溯状态,接着循环下去。
* 在循环中,[int i = h/i=0;这条语句在每次递归再次进入循环时都会得到执行]
* 【即for(int i = h/i=0; i
void combination(int[] nums, int k, int h) {
if (list.size()==k){res.add(new ArrayList<>(list));return;}
/**
* 通过终止条件,进行剪枝优化,避免无效的递归
* c中还剩 k - c.size()个空位,所以[ i ... n]中至少要有k-c.size()个元素
* 所以i最多为 n - (k - c.size()) + 1
* i <= n - (k - c.size()) + 1;
*/
for (int i = h; i <nums.length ; i++) {
list.add(nums[i]);
/**
*这里是i+1,不是h+1,否则会出现i=2,h=1,那么结果中会有【1,3,3】
* 当125添加后。i=nums.length,此时for结束,combination(nums,k,h+1,list);
* 即h+1少了一次执行机会,i就提前比h多加了一个1,i和h就从这里开始不同步了
*/
combination(nums,k,i+1);
list.remove(list.size()-1);
}
}
}
回溯法
正则表达式匹配【分类讨论思想】
origin link----回溯
dim—dp
- 有 * 【首字符匹配(*匹配多个)||首字符不匹配(*匹配0个)】,无 *【首字符匹配&&后续都要匹配】
- 程序终结的条件:【模式串为空,匹配串不为空,结果:fasle】,【模式串为空,匹配串为空,结果:true】
- 不断缩小字符串,重复执行以上步骤。
public boolean isMatch(String s, String p){
if (p.isEmpty()) return s.isEmpty();
boolean firstMatch=(!s.isEmpty()&&(s.charAt(0)==p.charAt(0)||p.charAt(0)=='.'));
if (p.length()>1&&p.charAt(1)=='*'){
return (firstMatch&&isMatch(s.substring(1),p))||isMatch(s,p.substring(2));
}else {
return firstMatch&&isMatch(s.substring(1),p.substring(1));
}
}
java算法api
- 获取二位数组的长和宽
int [][] array
有多少行: int r= array.length
有多少列 : int c=array[0].length
- 获得字符串的每个字符
for (int i = 0; i < str.length(); i++) {
char a = str.charAt(i);
}
- .substring(int beginIndex, int endIndex)
beginIndex - 开始处的索引(包括)
endindex 结尾处索引(不包括)- List< String>/Set< String> .contains(String)
string常用api
String str="abc";
/**
* "a.b.cd".split("\\.") 按照.将字符串切割成字符串数组["a","b","cd"]
* str.startsWith("a") 该字符串是否以a开头
* str.indexOf('a') 首次a字符所在的下标
* str.charAt('0') 获得指定下标的字符
* str.replace('a','q') 把a换成q,想替换所有可以用replaceAll();
* str.substring(0,2) 截取下标0~1的字串
* str.contains("ab") 是否包含字串ab
* str.concat("abc") 拼接字符串
* str.equalsIgnoreCase("ABC") 字符串相等?忽略大小写
* str.toUpperCase() 将字母小写全部转为大写
* str.codePointAt(0) 返回指定下标对应字符的10进制的值
*/
Arrays常用api
int[] nums=new int[]{1,2,3,4,5};
/**
* 常用api
*/
int[] ints = Arrays.copyOfRange(nums, 0, 2); //[1,2] //nums数组类型只能是基本类型
List<Integer> list = Arrays.asList(nums); //nums数组类型只能是包装类型
List<Integer> list1 = Arrays.asList(1, 2, 3);//将数组转为List,不过数组类型必须是包装类型
int index = Arrays.binarySearch(nums, 4); //返回匹配到元素的下标
Integer[] objects =(Integer[]) list.toArray() ; //list转数组
Stream<Integer> stream = Arrays.stream((Integer[]) list.toArray()); // list转stream流
优先队列【PriorityQueue】,优先hash【TreeMap】
public static void main(String[] args) {
TreeMap treeMap = new TreeMap<Integer,Integer>();
treeMap.put(10,10);treeMap.put(1,1);treeMap.put(3,3);
treeMap.get(treeMap.firstKey()); //获得值最小的key的value[结果是:1]
PriorityQueue<Integer>priorityQueue=new PriorityQueue<>();
priorityQueue.add(10);priorityQueue.add(1);priorityQueue.add(3);
System.out.println(priorityQueue.poll());//优先队列,本质就是小顶堆,弹出队头元素【结果是1】
PriorityQueue<Integer>priorityQueue1=new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
}); //构造大顶堆【优先队列】---自定义排序规则
}
- 去重重复的数组
// 建立去重的容器
Set<List<Integer>> result_set = new TreeSet<>(new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> o1, List<Integer> o2) {
//Arrays.sort(o1);Arrays.sort(o2);
for (int i = 0; i < o1.size(); i++) {
if (!o1.get(i).equals(o2.get(i))) return o1.get(i) - o2.get(i);
}
return 0;
}
});
[[1,2,3],[3,2,1],[1,1,1],[2,3,1]]
将元素相同的数组进行“去重”
A.containsAll(B) // A【1,2,3】集合是否全部包含者B【2,2,2】的元素-----true,它并不能解决上述问题
hashmap巧解题
无重复字符的最长子串
两数之和
位运算
&,|,~,^,>>,<<,>>>
java移位运算符<< 和 >> 和 >>>
dim-原码反码补码及加减运算
假设在8位的计算机上,整数数据类型占8位,数分为有符号【1位是符号位(0正1负),7位是数值位】和无符号数【8位都是数值位,即表示正整数】对于移位运算,先将数表示成8位的二进制的形式.左边是高位,右边是低位
" <<" 表示左移,不分正负数,低位补0;
" >>" 表示右移,如果该数为正,则高位补0,若为负数,则高位补1;
">>>"表示无符号右移,也叫逻辑右移,即若该数为正,则高位补0,而若该数为负数,则右移后高位同样补0
r = 20 << 2=80 【左移2位,即扩大2^2倍】
r = -20 << 2=-80 【对负数是绝对值扩大了】
r=20>>>1 =10【右移一位,即缩小了2倍】

一个数为n【n可能很大】
n&1 结果:0或1,【巧用 n&(n−1)求二进制中1的个数】
~做数的调整用的
^递归运算里面常用(不进位的二进制加法)
|待补充
例题:第K个语法符号
class Solution {
public int kthGrammar(int N, int K) {
if (N == 1) return 0;
return (~K & 1) ^ kthGrammar(N-1, (K+1)/2);
}
}
参考自己写的