2020 CCPC Wannafly Winter Camp Day5
Solved:2/10(A、E)
Rank:51/124
UpSolving:5/10(A、E、G、H、J)(I 待补)
https://ac.nowcoder.com/acm/contest/4120
A、Alternative Accounts
显然只有当3时需要处理一下,因为可能存在
1 2
2 3
1 3
显然,这组数据至少要3个人,所以我们需要判断这种情况即 在一二、二三、一三、一二三集合中的数量
#include
#define ll long long
#define sc scanf
#define pr printf
using namespace std;
vectorv[100005];
int main()
{
int n, k;
sc("%d%d", &n, &k);
int ans = 0;
for (int i = 0; i < k; i++)
{
int s, t;
sc("%d", &s);
ans = max(ans, s);
while (s--)
{
sc("%d", &t);
v[t].push_back(i);
}
}
if (k < 3)
pr("%d", ans);
else
{
int num[7];// 0 1 2 01 02 12 012
memset(num, 0, sizeof(num));
for (int i = 1; i <= n; i++)
{
if (v[i].size() == 3)
num[6]++;
else if (v[i].size() == 2)
{
if (v[i][0] == 1)
num[5]++;
else if (v[i][1] == 2)
num[4]++;
else
num[3]++;
}
else if (v[i].size() == 1)
{
num[v[i][0]]++;
}
}
ans = max(ans, num[3] + num[4] + num[5] + num[6]);
pr("%d\n", ans);
}
} E、Matching Problem
枚举前三个位置,加点剪枝,然后用前缀和求第四个位置的数量,不过要讨论的情况比较多。
#include
using namespace std;
const int N = 305;
#define ll long long
int c[N], nex[N][N];
int b[5], sum[N];
bool cmp(int a, int b) {
return a == b ? true : false;
}
int main() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &c[i]);
for (int j = 1; j <= n; j++)
nex[i][j] = nex[i - 1][j];
sum[i] = sum[i - 1] + 1;
nex[i][c[i]]++;
}
for (int i = 1; i <= 4; i++)
scanf("%d", &b[i]);
ll ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
if (cmp(c[i], c[j]) != cmp(b[1], b[2]))
continue;
for (int k = j + 1; k <= n; k++) {
if (cmp(c[i], c[j]) != cmp(b[1], b[2]) || cmp(c[i], c[k]) != cmp(b[1], b[3]) || cmp(c[k], c[j]) != cmp(b[3], b[2]))
continue;
if (b[4] == b[1]) {
ans += nex[n][c[i]] - nex[k][c[i]];
}
else if (b[4] == b[2]) {
ans += nex[n][c[j]] - nex[k][c[j]];
}
else if (b[4] == b[3]) {
ans += nex[n][c[k]] - nex[k][c[k]];
}
else {
int Sum = sum[n] - sum[k];
if (b[1] == b[2] && b[2] == b[3])
Sum -= nex[n][c[i]] - nex[k][c[i]];
else if (b[1] == b[2]) {
Sum -= nex[n][c[i]] - nex[k][c[i]];
Sum -= nex[n][c[k]] - nex[k][c[k]];
}
else if (b[1] == b[3]) {
Sum -= nex[n][c[i]] - nex[k][c[i]];
Sum -= nex[n][c[j]] - nex[k][c[j]];
}
else if (b[2] == b[3]) {
Sum -= nex[n][c[j]] - nex[k][c[j]];
Sum -= nex[n][c[i]] - nex[k][c[i]];
}
else {
Sum -= nex[n][c[i]] - nex[k][c[i]];
Sum -= nex[n][c[j]] - nex[k][c[j]];
Sum -= nex[n][c[k]] - nex[k][c[k]];
}
ans += Sum;
}
}
}
}
printf("%lld", ans);
} G、Cryptographically Secure PRNG
打表容易发现,答案是对称的。
但是这里有个坑点,答案是对称的,但不能在 i < sqrt(n) 停止,要在 inv(i) < sqrt(n) 的时候停止,只有当另一边大于等于根号时,我们才认为对称的一边已经全部求出来了。
#include
#define ll long long
#define sc scanf
#define pr printf
#define Pair pair
using namespace std;
ll inv[1000000];
int main()
{
int T;
sc("%d", &T);
while (T--)
{
vectorv;
ll p;
sc("%lld", &p);
inv[0] = 1;
inv[1] = 1;
ll maxn = 1e9 + 7;
ll sqrtp = sqrt(p);
for (int i = 2; i < p; i++)
{
inv[i] = inv[p % i] * (ll)(p - p / i) % p;
if (inv[i] < sqrtp)
break;
if (inv[i] < maxn)
{
maxn = inv[i];
v.push_back(Pair{ i,inv[i] });
v.push_back(Pair{ inv[i],i });
}
}
sort(v.begin(), v.end(), [](Pair q, Pair w) {
return q.first < w.first;
});
v.erase(unique(v.begin(), v.end()), v.end());
int len = v.size();
pr("%d\n", len);
for (int i = 0; i < len; i++)
pr("%lld %lld\n", v[i].first, v[i].second);
}
} H、Geometry PTSD
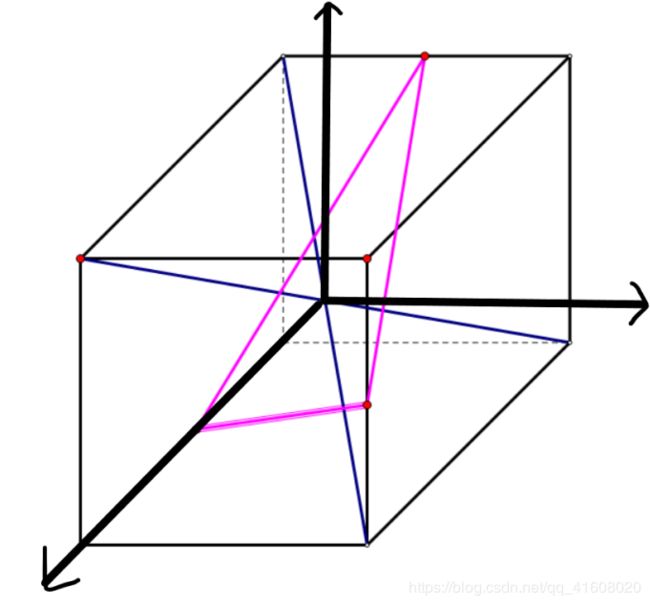
作出圆的外接球,构造出如图所示的经过圆点的等边三角形,然后暴力将一些点偏移,直到满足题目的要求。
#include
#define ll long long
#define sc scanf
#define pr printf
using namespace std;
int main()
{
pr("999999 1000000 0\n");
pr("-999997 0 999999\n");
pr("0 -999996 -999997\n");
} I、Practice for KD Tree
KD树占坑。
待补。
J、Xor on Figures
说白了就是n^2个正方形,每个位置非0即1,并且多个正方形组合的时候,相同位满足异或性质,求使用这 n^2 个正方形能构造出多少个不同的正方形。
赛时一直乱搞,搞到最后也没过,猜了无数个结论。
赛后发现可以线性基搞,考虑用Bitset维护一个正方形,然后维护一下bitset的线性基,将n^2个bitset插入,最后能构造出的不同正方形的数量就是 2^插入成功的个数(线性基的性质)
#include
#define ll long long
#define sc scanf
#define pr printf
using namespace std;
const int MAXN = 1100;
const ll mod = 1e9 + 7;
#define bt bitset
struct line_base
{
bt b[MAXN];
int cnt;
void init()
{
for (int i = 0; i < MAXN; i++)
b[i].reset();//0
cnt = 0;
}
void insert(bt val)
{
for (int i = 0; i < MAXN; i++)
{
if (val[i] == 1)
{
if (b[i].count() == 0)
{
b[i] = val;
cnt++;
break;
}
else
val ^= b[i];
}
}
}
};
line_base LB;
ll power(ll a, ll b)
{
ll res = 1;
while (b)
{
if (b & 1)
res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
ll a[33][33];
ll t[33][33];
bt temp;
char s[MAXN];
int main()
{
LB.init();
int n, k;
sc("%d", &k);
n = 1 << k;
for (int i = 0; i < n; i++)
{
sc("%s", s);
for (int j = 0; j < n; j++)
a[i][j] = s[j] - '0';
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
for (int k = 0; k < n; k++)
for (int l = 0; l < n; l++)
t[(i + k) % n][(j + l) % n] = a[k][l];
for (int k = 0; k < n; k++)
for (int l = 0; l < n; l++)
{
if (t[k][l])
temp.set(k * n + l);
else
temp.reset(k * n + l);
}
LB.insert(temp);
}
}
ll ans = power(2LL, LB.cnt);
pr("%lld\n", ans);
}