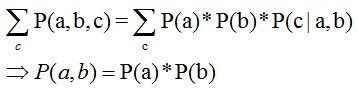贝叶斯网络三个结构
贝叶斯网络
一、
贝叶斯网络,由一个有向无环图(DAG)和条件概率表(CPT)组成。
贝叶斯网络通过一个有向无环图来表示一组随机变量跟它们的条件依赖关系。它通过条件概率分布来参数化。每一个结点都通过P(node|Pa(node))来参数化,Pa(node)表示网络中的父节点。
一个简单的贝叶斯网络,其对应的全概率公式为:
P(a,b,c)=P(c∣a,b)P(b∣a)P(a)
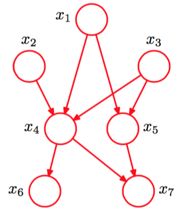
较复杂的贝叶斯网络,其对应的全概率公式为:
P(x1,x2,x3,x4,x5,x6,x7)=P(x1)P(x2)P(x3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)P(x7∣x4,x5)
二、
三种形式
head-to-head
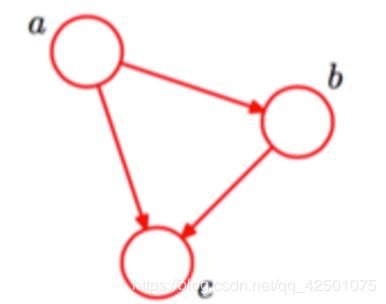
贝叶斯网络的第一种结构形式如下图
P(a,b,c) = P(a)*P(b)*P(c|a,b)成立,化简后可得:
在c未知的条件下,a、b被阻断(blocked),是独立的,称之为head-to-head条件独立
tail-to-tail
第二种结构形式如下图
考虑c未知,跟c已知这两种情况:
在c未知的时候,有:P(a,b,c)=P©*P(a|c)*P(b|c),此时,没法得出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
在c已知的时候,有:P(a,b|c)=P(a,b,c)/P©,然后将P(a,b,c)=P©*P(a|c)*P(b|c)带入式子中,得到:P(a,b|c)=P(a,b,c)/P© = P©*P(a|c)*P(b|c) / P© = P(a|c)*P(b|c),即c已知时,a、b独立。
所以,在c给定的条件下,a,b被阻断(blocked),是独立的,称之为tail-to-tail条件独立
head-to-tail
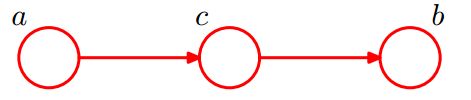
贝叶斯网络的第三种结构形式如下图
还是分c未知跟c已知这两种情况:
c未知时,有:P(a,b,c)=P(a)*P(c|a)*P(b|c),但无法推出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
c已知时,有:P(a,b|c)=P(a,b,c)/P©,且根据P(a,c) = P(a)*P(c|a) = P©*P(a|c),可化简得到:
在c给定的条件下,a,b被阻断(blocked),是独立的,称之为head-to-tail条件独立。
head-to-tail是一个链式网络
xi+1的分布状态只和xi有关,和其他变量条件独立。通俗点说,当前状态只跟上一状态有关,跟上上或上上之前的状态无关。这种顺次演变的随机过程,就叫做马尔科夫链(Markov chain)