学习笔记

文章 Diamond Radio Receiver: Nitrogen-Vacancy Centers as Fluorescent Transducers of Microwave Signals

氮空位色心（NV色心）

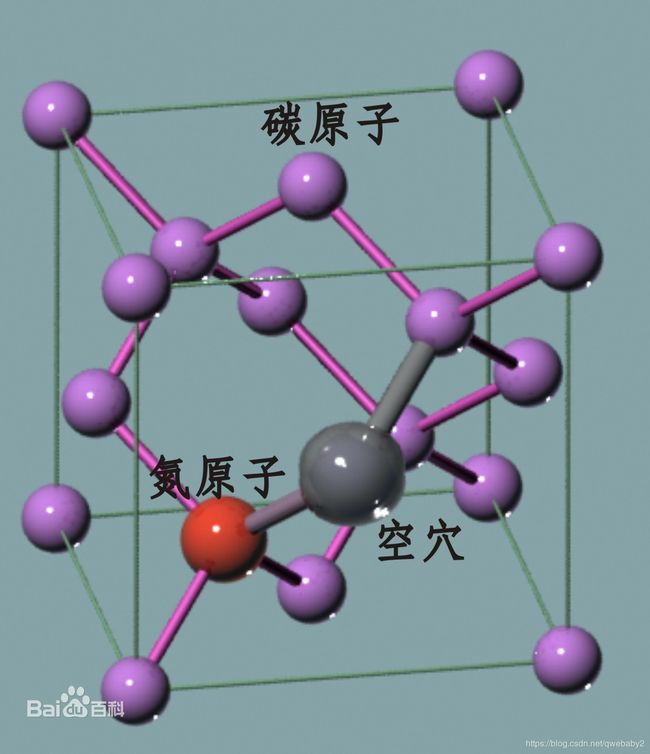
如图，金刚石结构是由碳原子按四面体成键方式互相连接，组成无限的三维骨架，是典型的原子晶体。每个碳原子都以SP3杂化轨道与另外4个碳原子形成共价键，构成正四面体。NV色心是金刚石中的一种发光点缺陷。一个氮原子取代金刚石中的碳原子，并且在临近位有一个空穴，这样的点缺陷被称为NV色心。

背景

因为无线通信的需要，发射机和接收机需要在一些极端条件下工作。除了传统的信号接收器外，基于NV色心的金刚石探测器可以在高压高达60 GPa，高温超过600 K，以及腐蚀性环境下工作，所以受到额外关注。

主要工作

介绍了一种基于NV色心的信号接收器，它能够解调FM无线电信号并将其转换成AM光学荧光信号。这一装置主要利用了NV色心的光致发光性是依赖于它的电子自旋状态的特点，而NV色心的电子自旋状态对微波辐射很敏感。这种金刚石收音机的带宽为91KHz。

光致发光：光致发光是指物体依赖外界光源进行照射，从而获得能量，产生激发导致发光的现象，它大致经过吸收、能量传递及光发射三个主要阶段，光的吸收及发射都发生于能级之间的跃迁，都经过激发态。而能量传递则是由于激发态的运动。紫外辐射、可见光及红外辐射均可引起光致发光。如磷光与荧光。

实验原理和系统

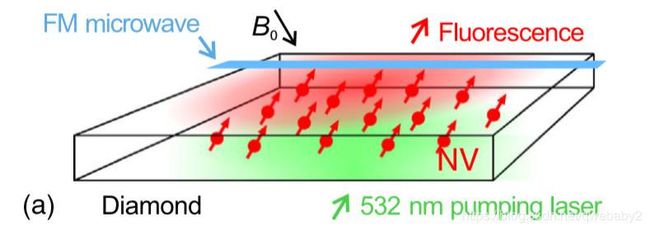
如图，实验系统是一个高温高压的金刚石板，带有高密度的NV色心。NV色心能解调调频微波信号，将其映射到荧光上。

先把金刚石样品用4.5 MeV的电子辐照2小时，在800℃退火16小时，然后在1200℃退火2小时。

然后，金刚石芯片被一个绿色(532 nm)激光连续激发;激发光斑是大约20mW，被照射的金刚石样品区域的直径为200 μm。（金刚石中带有负电荷的氮-空位发光中心（色心）的电子自旋可以用532纳米的激光来进行极化。色心电子自旋量子数为1，在零磁场下，m=0与m=±1之间的能级劈裂为2.87GHz，m=±1两个能级是简并的。）

能级劈裂：不同的状态由于体系的对称性等因素的约束而具有相同的能量，这叫简并。
当外场破坏系统的对称性时，简并被破坏，各个状态不再具有相同的能量，发生能级的劈裂。
例子：
1、塞曼效应，磁场导致的能级劈裂
2、stark效应，电场导致的能级劈裂

电磁铁用来提供一个直流的磁场，这个磁场的方向沿一个NV类的轴，而这个NV色心决定了金刚石接收器的对应的载频。这个磁场用来对接收信号的载频进行调谐（把荧光强度随频率变化的曲线搬移？）。

微波信号通过接触金刚石表面的微带波导传递到金刚石芯片上。微带处于表面的玻璃上，20 μm宽。

虽然色心所发射的荧光光谱比较宽，从637纳米到800纳米都有分布，但是其零声子谱线是很窄的，在637纳米附近。所以，金刚石接收器所发出的NV荧光被Olympus的设备所收集，经过Semrock StopLine 的滤波器（滤除532nm的波，通过632.8nm的波）由New Focus 的光检测器所检测，对剩下的色心发出的荧光进行探测，从而确定色心电子自旋的状态。通过检测荧光，可以得到设备的FM分辨率。

与目前广泛使用的脉冲激光实验系统相比，这种连续的光照射激发能够连续检测输入的微波信号，而且金刚石样品中NV色心密度很高。这种高密度NV色心的相干时间比散乱的NV色心短，但它能产生更强的信噪比。

NV色心所发出的荧光的光谱强度与NV色心的电子自旋状态有关系。

退火：将金属加热到一定温度，保持足够时间，然后以适宜速度冷却，通常是缓慢冷却，有时是控制冷却的一种金属热处理工艺。

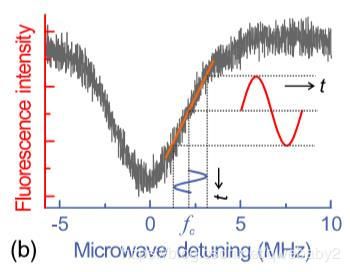
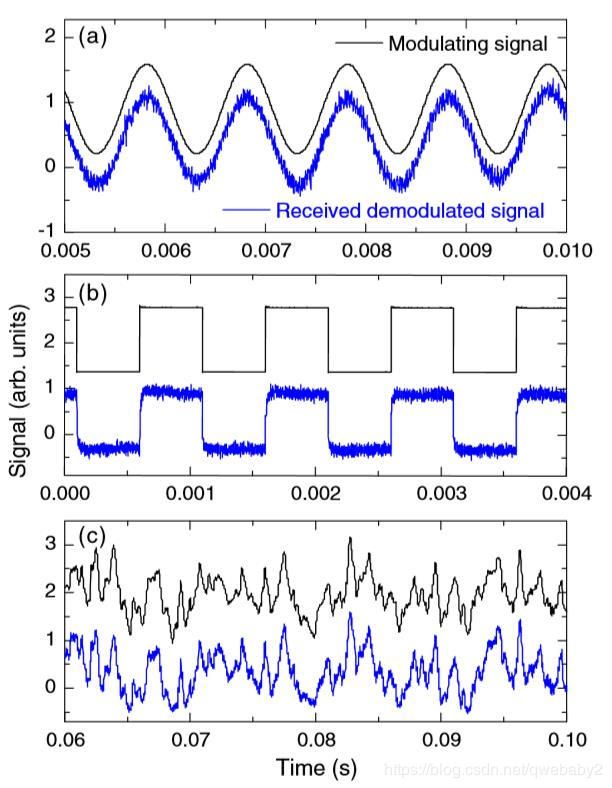
如图，当微波频率fm扫过NV色心基态次能级的共振频率f0时，荧光强度会下降。所以，FM金刚石接收器的解调原理是，当载波频率fc在斜率为正的一段时，微波信号的频率会正比例地映射成荧光的强度。

如图，当FM信号频率高的时候，荧光强度也高，FM信号频率低的时候，荧光强度也低。

使用NV色心接收由2.85ghz载波携带的FM无线电信号，然后微波信号通过微带被传送到NV色心。用带有调制信号的示波器对NV中心的红色荧光进行滤波、检测和监测。电磁铁施加一个直流磁场，将光学探测到的磁共振(ODMR)磁倾角移至该位置，从而使载频与NV微波共振的蓝色失谐，这样，接收到的信号与原调制信号同相位。

实验结果很好的验证了调制信号与解调信号相位相同。

文章 Assessment of Rydberg atoms for wideband electric field sensing

里德伯原子：高激发原子是一个价电子被激发到高量子态（主量子数n很大）的原子，也被称为里德伯原子。

背景

基于Rydberg原子的电测量能够在很大的频率范围内(从千兆赫到太赫兹)以高灵敏度进行可跟踪的电场测量，这种测量方法特别适用于射频和太赫兹设备的校准。
近年来，里德伯原子作为电场传感器的候选对象，其具有许多优点，引起了人们极大的兴趣。
1.里德伯原子是已知的确定量子粒子，许多反应与基本常数直接相关。
2.在超宽频率范围内表现出较大的极化率和灵敏度，对电场具有极其敏感。
3.体积很小，易获取。
4.与光学/激光技术兼容。
Rydberg传感器的潜力巨大，应用很多，但是到目前为止，还没有对其在宽光谱范围的灵敏度有一个定量的分析，尤其是与现存的其他电场传感技术相比。

主要工作

通过计算Rydberg传感器的工作频谱的场灵敏度来进行分析，并与基于EO晶体和传统无源电子的，类似尺寸(1cm)传感器进行比较。先讨论这些系统在操作上的基本差异，然后分析推导出在小电流、低频情况下的灵敏度。重点是典型模型系统的基础灵敏度极限，同时突出各种不同的特征。之后，提出了一个更一般的，数值处理的Rydberg传感器，以计算1THz以下的任意频率的场的灵敏度。通过实验验证了模型对1 - 20GHz频率范围的计算。

对于任意的电场传感器，测量过程可以分为三个阶段：
1.状态准备，包括入射场传感器的的模态成形和/或传感器初始化
2.场和传感器的交互，用宏观磁化率(χ)或微观极化率(α)参数来衡量
3.传感器读出
.
载波频谱范围：系统的工作载波频率范围
瞬时带宽：系统对其敏感的载波的最大变化率

不同系统间的差异：Rydberg原子和EO晶体具有较大的载波频谱范围，而偶极耦合无源电子传感器通常会受限，因为阻抗匹配偶极子读出负载具有挑战性。相比之下，无源电子传感器的瞬时带宽通常等于载波频谱范围，因此在这项技术中两者几乎没有区别。EO和Rydberg传感器的瞬时带宽通常受到读出过程的限制。对于EOs，这对应于光检测器的带宽。

暂时只看到这，许多基础知识不懂，很多概念看不明白。还是回去补补量子理论的知识吧。