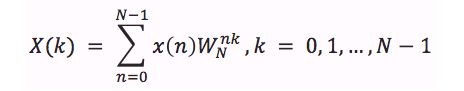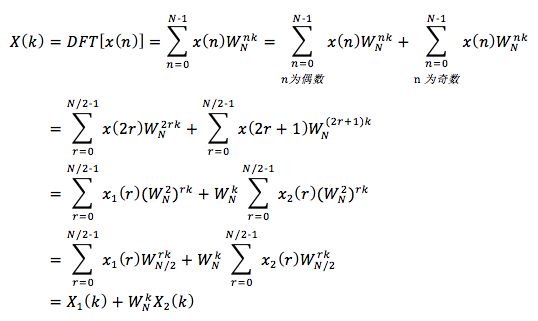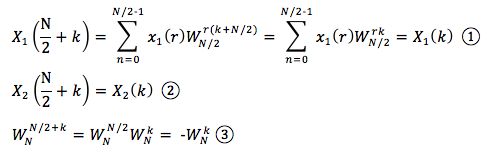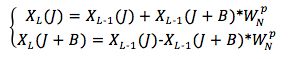数字信号处理公式变程序（一）——DFT、FFT

之前搞了一些数字信号处理算法编程（OC），一直没来得及整理，现在整理一下。陆续会更新，包括FFT、巴特沃斯滤波器（高低带通、高低带阻）、数据差值（线性、sinc、三次样条*）、数据压缩（等距、平均、峰值检测）和模仿matlab的STFT功能（spectrogram函数三维绘图）。

 

注：可能会有不足或者理解偏差的地方，路过的高人请不吝赐教。

 

好啦，进入正题。

---------------------------------------------------------------------------------------

在数字世界中FFT的意义不言而喻（我曾转载一篇文章有提到：http://blog.csdn.net/shengzhadon/article/details/40539101），这里就不再赘述了。FFT（快速傅里叶变换）是DFT的一种特殊情况，就是当运算点的个数是2的整数次幂的时候进行的运算（不够用0补齐），那就先从DFT开始吧。

 

一、DFT（本部分就是翻译公式）

定义（来自百科）：离散傅里叶变换（Discrete Fourier Transform，缩写为DFT），是傅里叶变换在时域和频域上都呈离散的形式，将信号的时域采样变换为其DTFT的频域采样。在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT，也应当将其看作其周期延拓的变换。在实际应用中通常采用快速傅里叶变换计算DFT。

 

DFT的公式是：设x(n)为M点的有限长序列，即在0≤n≤M-1内有值，则定义x(n)的N点（N≥M。当N＞M时，补N-M个零值点），离散傅里叶变化定义为

其中，为旋转因子（为方便编辑后续记作W(N, nk)，特此说明），其计算公式为，具有以下性质：

①周期性：W(N, nk) = W(N, (n+rN)k) = W(N, n(k+rN))，其中r问整数。

②共轭对称性：(W(N, nk))* = W(N, -nk)。

③可约性：W(N, nk) = W(mN, mnk)，W(N, nk) = W(N/m, nk/m)，其中m为整数，N/m为整数。

④特殊值：

W(N, N/2) = -1；  W(N, (k+N/2)) = -W(N, k)；  W(N, (N-k)n) = W(N, (N-n)k) = W(N, -nk)。

所以，在计算旋转因子的过程中可以适当的使用特殊值来提高运算的效率。

 

在计算DFT时，如果数据的点数够计算的点数，则截取计算点数长的数据进行DFT运算，否则将数据点个数补0至计算点个数，然后进行计算，举例如下（举例只是为了说明问题，没有按照编程语言的书写格式）。

比如：数据点数组为 dataArray = {1， 2， 3， 4，5}，可以看出数据长度为5。

   如果要求做4点DFT运算，则只需截取前4个数作为运算数组进行运算即可，即为{1， 2， 3， 4}；

   如果要求做8点DFT运算，则需在原数组后补三个0，使长度为8后再进行计算，计算数组为{1， 2， 3， 4，5，0，0，0}。

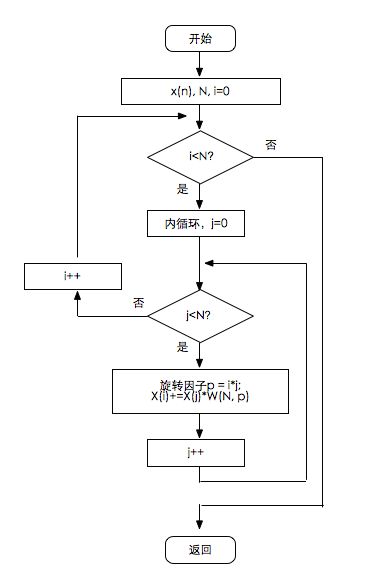
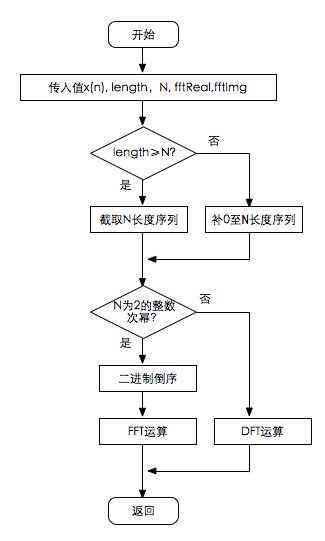
DFT流程图如下：

 

 

二、FFT

 

 

1.DFT的运算量

复数乘法次数为N*N，复数加法次数为N(N-1)，若N>>1，则这两者都近似为N*N，它随N增大为急速增大。

改进途径：①利用旋转因子性质减小计算量；②由于运算量和N*N成正比，因而可将N点DFT分解成小点数的DFT，以减少运算量（点数越小，计算量越小）；③改为用FFT计算，复数乘法次数为(N/2)*log(2,N)。

 

2.FFT可分为按照时间抽选的基-2算法（库利-图基算法DIT-FFT）和按频率抽选的基-2算法（桑德-图基算法DIF-FFT）。本文采用DIT-FFT算法。

 

3.FFT计算原理及流程图

FFT的计算要求点数必须为2的整数次幂，如果点数不够用0补齐。例如计算{2，3，5，8，4}的8点FFT，需要补3个0后进行计算，如果计算该数组的5点FFT，则先计算8点FFT后截取前5个值即可（不提倡）。

 

（1）原理

公式推导

设序列x(n)点数为N=2^L，L为整数。将N=2^L，先按照n的奇偶分为两组，其中r = 0, 1, ..., N/2-1

x(2r) = x1(r)

x(2r-1) = x2(r)

则可将DFT化为（式1）

由上式可以看出一个N点的DFT可以分为两个N/2点的DFT，按照上式右组合成N点DFT。但是这里的x1(r)、x2(r)以及X1(k)、X2(k)都是N/2点的序列，即r,k满足r,k=0, 1, ..., N/2-1。而X(k)却有N点，上式计算的只是X(k)的前半项数的结果，因此还需要计算后半项的值。

将①②③代入（式1），就可将X(k)表达为前后两部分：

前半部分，X(k)，当k=0, 1, ..., N/2-1

后半部分，X(k)，当k=N/2, ..., N-1

蝶形运算说明

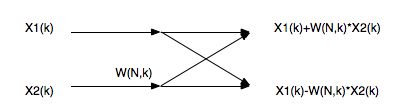
蝶形运算，符号表示如下图所示：

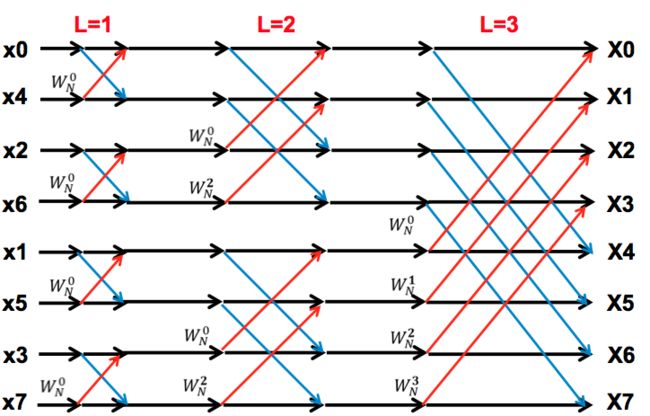
所以，FFT的蝶形运算图表示为（8点，2^3 = 8，运算级数最大为L=3）

在蝶形运算中变化规律由W(N, p)推导，其中N为FFT计算点数，J为下角标的值

L = 1时，W(N, p) = W(N, J) = W(2^L, J)，其中J = 0;

L = 2时，W(N, p) = W(N, J) = W(2^L, J)，其中J = 0, 1;

L = 3时，W(N, p) = W(N, J) = W(2^L, J)，其中J = 0, 1, 2, 3;

所以，W(N, p) = W(2^L, J)，其中J = 0, 1, ..., 2^(L-1)-1

又因为2^L = 2^M*2^(L-M) = N*2^(L-M)，这里N为2的整数次幂，即N=2^M，

W(N, p) = W(2^L, J) = W(N*2^(L-M), J) = W(N, J*2^(M-L))

所以，p = J*2^(M-L)，此处J = 0, 1, ..., 2^(L-1)-1，当J遍历结束但计算点数不够N时，J=J+2^L，后继续遍历，直到计算点数为N时不再循环。

举例：N=8点的FFT计算

当L=2时，J = 0, 1两个值，因此p = J*2^(M-L) = 0, 2两个值，即旋转因子有两个值W(8, 0)和W(8, 2)，计算中两行之间的距离B = 2^(L-1)=2^(2-1)=2，

代入J=0, 1可求得X(0)、X(0+2)和X(1)、X(1+2)，即可求出第2级蝶形运算的X(0), X(1), X(2), X(3)，也就是求出一半，此时J加步进2^L=4，即J=J+2^L=4, 5，

再代入J=4, 5可求出X(4), X(4+2)和X(5), X(5+2)，即可求出第2级蝶形运算的X(4), X(5), X(6), X(7)，已经全部求出，J循环结束。

 

二进制倒序说明

前面数的排列顺序是进行二进制倒序后的排序。二进制倒序是指将某数转化为二进制表示，将最高位看做最低位、次高位看做次低位...以此类推，计算后的纸进行排序。例如3的二进制表示为011b（3=0*2^2+1*2+1），二进制倒序值为6（011b，最高位看做最低位...即6=0+1*2+1*2^2）

即0到7的二进制排序是：

       0,                4,                 2,                6,                 1,                5,                3,                7

000→000    001→100    010→010    011→110    100→001    101→101    110→011    111→111

 

（2）流程图

①FFT运算总流程图，包括

②根据（1）中推导的内容，FFT的流程图可化为

 

说明：蝶形运算中又三层循环

第一层（最外层），完成M次迭代过程，即算出A0(k), A1(k), ..., Am(k)，其中k=0, 1, ..., N；A2(k)为蝶形运算第2级的结果，如A0(k)=x(k), Am(k)=X(k)；

第二层（中间层），完成旋转因子的变化，步进为2^L；

第三层（最里层），完成相同旋转因子的蝶形运算。

三、DFT、FFT测试结果

 

 

 

 

 

本文开头就已经说了，我个人比较喜欢使用matlab，所以我程序的对比对象当然是matlab。给定t1[8] = {0,1,2,3,4,5,6,7};signal=sin(t1);对signal进行8、16、4、13、6点FFT/DFT计算输出的结果和给定128点数据进行128点FFT计算结果如下图所示：

 

复制一遍：

FFT，8点计算结果

0.553733 + 0.000000i   2.394647 - 2.097012i   -1.386684 + 0.915560i   -0.881042 + 0.280414i   -0.807574 + 0.000000i   -0.881042 - 0.280414i   -1.386684 - 0.915560i   2.394647 + 2.097012i   

FFT，16点计算结果

0.553733 + 0.000000i   1.431957 + 0.493527i   2.394647 - 2.097012i   -1.786256 - 2.899550i   -1.386684 + 0.915560i   0.105162 - 0.495158i   -0.881042 + 0.280414i   0.249137 - 0.129291i   -0.807574 + 0.000000i   0.249137 + 0.129291i   -0.881042 - 0.280414i   0.105162 + 0.495158i   -1.386684 - 0.915560i   -1.786256 + 2.899551i   2.394647 + 2.097012i   1.431957 - 0.493527i   

FFT，4点计算结果

1.891888 + 0.000000i   -0.909297 - 0.700351i   -0.073294 + 0.000000i   -0.909297 + 0.700351i   

FFT，13点计算结果

0.553733 + 0.000000i   1.898167 + 0.288124i   0.803761 - 3.465451i   -2.328951 + 0.137430i   0.200269 - 0.367077i   -0.688243 + 0.477332i   -0.161869 - 0.528187i   -0.161868 + 0.528186i   -0.688245 - 0.477332i   0.200271 + 0.367075i   -2.328952 - 0.137428i   0.803762 + 3.465451i   1.898167 - 0.288123i   

FFT，6点计算结果

0.176162 + 0.000000i   -0.276095 - 3.002073i   0.123599 - 0.116304i   0.128828 + 0.000000i   0.123600 + 0.116302i   -0.276092 + 3.002073i   

FFT，128点计算结果

0.699691 + 0.000000i   0.704772 + 0.010352i   0.719298 + 0.021364i   0.739474 + 0.033697i   0.749607 + 0.047746i   0.679161 + 0.061398i   0.105405 + 0.050647i   -6.945906 - 0.423135i   54.641422 + 5.062080i   -57.156776 - 6.630915i   9.187446 + 1.338868i   0.342783 + 0.093026i   -0.288066 - 0.020889i   -0.353394 - 0.043726i   -0.328844 - 0.047995i   -0.290196 - 0.047167i   -0.253328 - 0.044825i   -0.221405 - 0.042109i   -0.194470 - 0.039423i   -0.171855 - 0.036897i   -0.152811 - 0.034570i   -0.136679 - 0.032440i   -0.122920 - 0.030495i   -0.111105 - 0.028715i   -0.100891 - 0.027084i   -0.092007 - 0.025581i   -0.084229 - 0.024193i   -0.077390 - 0.022905i   -0.071342 - 0.021706i   -0.065971 - 0.020587i   -0.061182 - 0.019537i   -0.056895 - 0.018550i   -0.053044 - 0.017619i   -0.049575 - 0.016737i   -0.046441 - 0.015901i   -0.043601 - 0.015106i   -0.041024 - 0.014347i   -0.038679 - 0.013621i   -0.036542 - 0.012927i   -0.034593 - 0.012260i   -0.032808 - 0.011617i   -0.031181 - 0.010997i   -0.029686 - 0.010398i   -0.028318 - 0.009818i   -0.027066 - 0.009256i   -0.025917 - 0.008710i   -0.024865 - 0.008177i   -0.023903 - 0.007660i   -0.023024 - 0.007153i   -0.022220 - 0.006657i   -0.021489 - 0.006172i   -0.020825 - 0.005695i   -0.020224 - 0.005227i   -0.019682 - 0.004767i   -0.019197 - 0.004313i   -0.018766 - 0.003867i   -0.018383 - 0.003419i   -0.018055 - 0.002986i   -0.017772 - 0.002551i   -0.017534 - 0.002121i   -0.017342 - 0.001693i   -0.017193 - 0.001268i   -0.017087 - 0.000845i   -0.017025 - 0.000423i   -0.017003 + 0.000000i   -0.017025 + 0.000422i   -0.017087 + 0.000845i   -0.017193 + 0.001268i   -0.017342 + 0.001693i   -0.017534 + 0.002121i   -0.017772 + 0.002551i   -0.018055 + 0.002986i   -0.018383 + 0.003425i   -0.018766 + 0.003866i   -0.019197 + 0.004314i   -0.019682 + 0.004767i   -0.020224 + 0.005227i   -0.020825 + 0.005695i   -0.021489 + 0.006172i   -0.022220 + 0.006656i   -0.023024 + 0.007153i   -0.023902 + 0.007659i   -0.024865 + 0.008177i   -0.025917 + 0.008710i   -0.027066 + 0.009256i   -0.028318 + 0.009818i   -0.029686 + 0.010398i   -0.031179 + 0.010998i   -0.032808 + 0.011617i   -0.034592 + 0.012259i   -0.036542 + 0.012927i   -0.038679 + 0.013621i   -0.041024 + 0.014347i   -0.043601 + 0.015106i   -0.046441 + 0.015901i   -0.049574 + 0.016737i   -0.053044 + 0.017619i   -0.056894 + 0.018549i   -0.061182 + 0.019537i   -0.065971 + 0.020587i   -0.071342 + 0.021706i   -0.077390 + 0.022905i   -0.084229 + 0.024193i   -0.092005 + 0.025579i   -0.100891 + 0.027084i   -0.111107 + 0.028715i   -0.122921 + 0.030496i   -0.136679 + 0.032441i   -0.152811 + 0.034570i   -0.171855 + 0.036897i   -0.194470 + 0.039423i   -0.221401 + 0.042109i   -0.253328 + 0.044825i   -0.290195 + 0.047166i   -0.328844 + 0.047996i   -0.353394 + 0.043726i   -0.288066 + 0.020889i   0.342783 - 0.093026i   9.187446 - 1.338871i   -57.156776 + 6.630923i   54.641422 - 5.062086i   -6.945903 + 0.423136i   0.105404 - 0.050648i   0.679161 - 0.061398i   0.749607 - 0.047746i   0.739474 - 0.033698i   0.719298 - 0.021364i   0.704768 - 0.010354i 

 

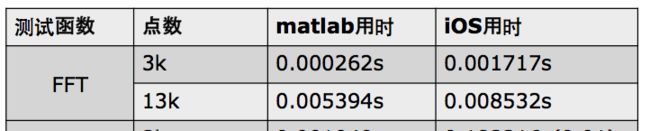
测试结果显示：iOS程序与MATLAB程序运算结果一致，但是MATLAB运算效率高。以下是多次比较求平均后的时间值

 

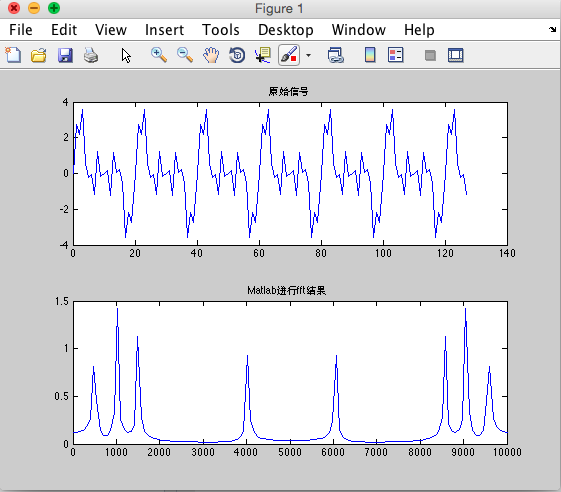
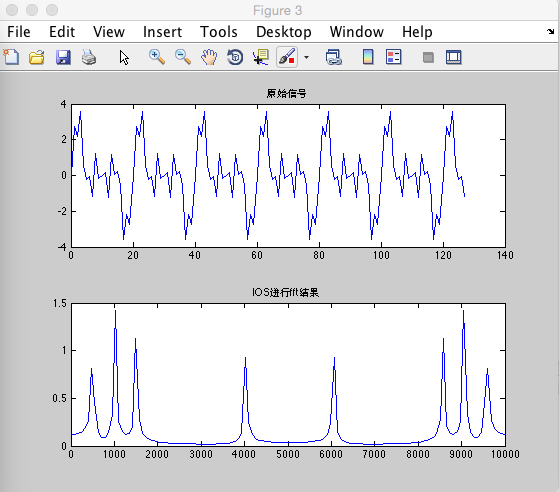
为了更直观的观察，将其他的信号（几个信号叠加后的信号）通过fft计算后并作频域处理导入matlab，绘制图如下：

 

===================================================================

OK，FFT随笔一份，方便自己以后查阅。其中一定会有很多不足，望路过的大神订正。谢过