深度学习入门(上)-第一章 必备基础知识点
1.深度学习与人工智能简介
大数据时代造就了人工智能的发展,人工智能的时代已经来临。数据规模越大,深度学习算法越好。深度学习有诸多应用,如诉说图片故事,自动驾驶等等。
2.CV面临的挑战与常规套路
图像分类是CV核心任务。图片是由若干个像素点组成的,一张图片被表示成3维数组的形式,每个像素的值[0,255]。像素点与亮度有关,像素点值越大,亮度就越大。
挑战:viewpoint variation, illumination conditions, scale variation, deformation, background clutter, occlusion, intra-class variation.
常规套路:数据驱动方法,即
- 收集data并打label。(将data和label进行一一对应的操作)
- train一个分类器。在deep learning 中,这个分类器就是神经网络。
- test 和评估。
def train(train_images, train_labels):
# build a model for images-labels..
return model
def predict(model, test_images):
# predict test_labels using the model..
return test_labels3.用K近邻来进行图像分类
指定K值,看当前物体离谁比较近,离谁近的越多,我们就说等于谁。
KNN运作流程
- 对于未知类别属性数据集中的点与当前点的距离
- 按照距离依次排序
- 选取与当前点距离最小的K个点
- 确定前K个点所在类别的出现概率
- 返回前K个点出现频率最高的类别作为当前点的预测分类
KNN特点:
简单有效,lazy-learning
无训练操作。分类器不需要使用training set进行training,训练时间复杂度为0.
KNN分类的计算复杂度和traing set中的文档数目成正比,即若training set中文档总数为n,那么KNN的分类时间复杂度为0(n).
KNN算法的三个基本要素:K值的选择,距离度量,分类决策规则。
KNN方法在分类时的主要不足:当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。
解决方法:不同的样本给予不同的权重。
此外,KNN算法虽然简易,但需要存储所有的training data,且在test时过于耗费计算能力。
为了用很小的时间代价,把分类任务完成,推荐使用CIFAR-10数据集,介绍:10类标签(airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck),50000个training data,10000个test data,大小均为32*32.
如何用KNN进行图像分类呢?
- 计算距离:

用K近邻算法做图像分类的代码实现(k=1):
Note:仅仅使用L1或者L2进行像素比较是有问题的,图像更多的是按照背景和颜色被分类,而不是语义主体本身,所以不提倡使用这种方法完成图像分类的任务。
import numpy as np
class NearestNeighbor:
def __init__(self):
pass
def train(self, X, y):
# knn无须训练,所以直接把数据和标签存起来即可
self.Xtr = X
self.ytr = y
def predict(self, X):
# 对于每一个测试数据,在training data中找出与其L1距离最小的样本的标签,作为其标签。
num_test = X.shape[0]
Ypred = np.zeros(num_test, dtype = self.ytr.dtype)
for i in xrange(num_test):
distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
min_index = np.argmin(distances)
Ypred[i] = self.ytr[min_index]
return Ypred这里,L1距离实际上是一种超参数
4.超参数与交叉验证
距离是一种超参数。 
现在有一些关于超参数的问题。
- 如何设定距离,使用L1还是L2?
- KNN中K如何选择?
- 如果有其他超参数的话,如何设定其他超参数?
解决方法:
首先要明确的是:test set是非常宝贵的,不能用测试集调节参数,test set只能最后用。所以,往往采用交叉验证的方式来找到合适的参数。推荐使用交叉验证的方式来进行模型的建立。 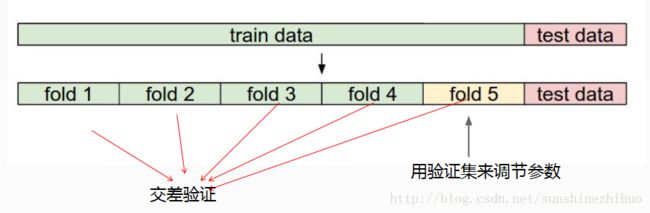
1.选取超参数的正确方法是:将原始training set分为training set 和 validation set,在验证集上尝试不同的超参数,随后选取最优超参数。
2.若训练数据不够,可使用交叉验证的方法,帮助在选取最优超参数时减少噪声。
3.一旦找到最优超参数,就让算法以该参数在test set上跑,且只跑一次。然后,根据测试结果评价算法。
5.线性分类
还是做分类这件事,要得到属于每个类别的概率值(得分值)。 
将原图拉伸为3072个像素点。32*32*3=3072。 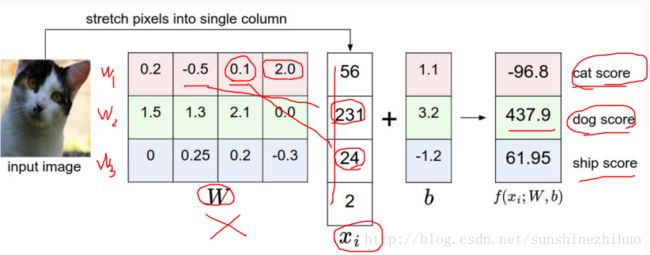
权重参数决定当前像素点产生的是积极作用还是消极作用。得分值最高的就是分类结果,很明显,本例分类结果出错了。
6.损失函数
预测错了,需要改正过来。知错能改,离不开损失函数。
能够用什么样的标准来评估当前的损失呢? 
用什么标准来评判当前的损失?
SVM损失函数:正确得分值与其他所有错误类别得分值的差异情况。1代表可容忍的程度。得分值相减的结果,比0大就意味着有损失,比0小就意味着没有损失。用损失函数来衡量当前模型的效果如何。
Note:这里使用是得分值。
我们要算的是Model的效果,所以要把所有的样本都算出来。随后除以N,因为,一个模型的好坏是与拿多少样本进行测试是没有关系的。
7.正则化惩罚项 
对W的惩罚力度小,说明认可。
损失函数终极版:Loss = data loss + 正则化惩罚项loss 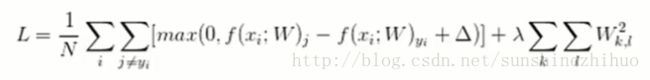
至此,我们知道了应该怎样来评判一个模型!
8.softmax分类器
SVM输出的是一个得分值,Softmax输出的是概率。得分值其实不太直观,在进行多类别分类时,我们提倡使用Softmax分类器,所有类别的概率值加起来必定等于1。
Sigmoid函数: 
因为Sigmoid函数y的取值范围是(0,1),所以可以对于任意x的输入,将结果映射为概率。可以用于经典的2分类问题。输入x:得分函数。将得分函数映射到当前的Sigmoid中,就可以得到最终的概率值。再通过概率值(结合0.5)进行分类就OK。
Softmax分类器
Softmax分类器做了一个归一化的操作 
Softmax分类器要对wx+b得到的得分值进行指数映射exp(让大的得分值更大,小的得分值更小),然后再进行归一化操作normalize。这样就得到了属于类别的概率值。(用softmax分类器最终得到的是概率值)
关于当前loss,是对于正确类别的概率进行负对数操作。(用正确类别的概率值进行loss的计算) 
两种损失函数的对比
SVM和Softmax 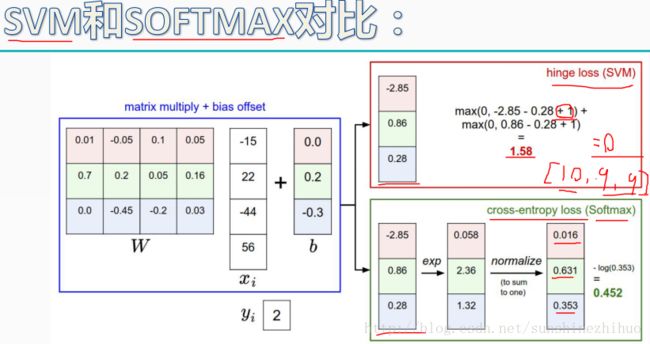
hinge loss(SVM)不常用,因为当正确类别的得分和错误类别的得分差异不大时,区分不是很精细,甚至可能出现loss=0,但分类效果不太好的情况。而Softmax分类器是一个永远不知道满足的分类器,总是会有Loss的。
9.最优化 
有了loss之后,就可以进行最优化的操作了。
最优化是在神经网络的反向传播中提出来的。
10.梯度下降算法原理
前向传播:from x to loss
用梯度下降的方法来求解神经网络。
Batchsize通常是2的整数倍(32,64,128),此值与计算机所能够承受的负载量有关系。
Epoch:跑完一遍train set的所有数据,就叫做一个epoch。要跑完所有的数据。
iter:一次迭代是对一个batch中的数据进行前向传播和反向传播的过程。要跑完一个batch。
学习率:当进行反向传播调节参数的时候,让网络模型进行一个自我的学习,学习的时候用梯度下降来求解,那一次学多大呢?用学习率来定义。
通过小的学习率和大的迭代次数来完成神经网络的操作。
weights += -step_size * weights_grad11.反向传播
通常情况下,对权重w进行随机初始化,然后再进行优化的操作。
反向传播:在求出loss之后,通过反向传播进行权重参数的优化,以使得loss最低。在反向传播的过程中需要决定什么样的w该更新,更新力度如何。核心任务:更新权重参数。 
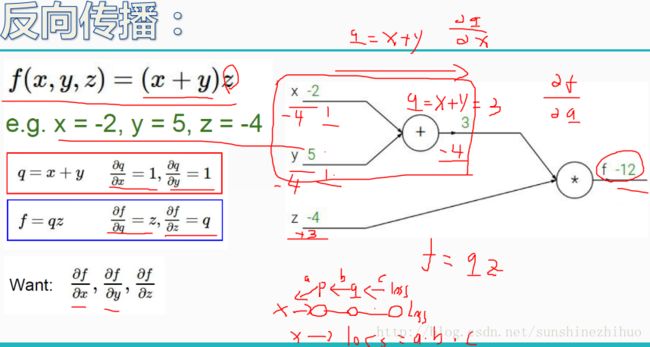
要算x,y,z分别对f做了多大的贡献。相当于权重参数对最终的loss值的影响。
-4的意思是,q上升1倍会使得f下降4倍。 
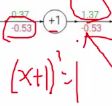
上图中每个操作是明确的,对每个操作都可以算个导数。以最后一个节点为例,把1.37传进来,代入偏导式中,得到-0.53。 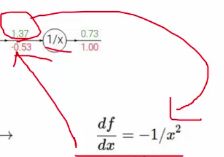

最终可以算出w0, w1, w2对loss产生了多大的贡献,之后进行相应改变,更新权重参数。
将问题进一步简化: 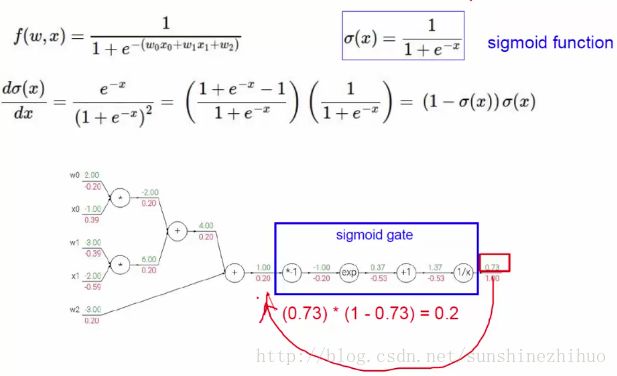
梯度分配:
加法门单元:均等分配
Max门单元:给最大的,被忽略掉的那个,反传的梯度为0
乘法门单元:互换 
