自适应谐振理论网络|ART

自适应谐振理论网络|ART

自适应谐振理论（Adaptive Resonance Theory,简称ART）网络是由美国Boston大学学者 G. A.Carpenter在1976年提出。多年来，G. A.Carpenter一直试图为人类的心理和认知活动建立统一的数学理论， ART 就是这一理论的核心部分。随后 G. A.Carpenter 又与 S.Grossberg 提出了ATR 网络。 经过了多年的研究和不断发展，ART 网已有 ３ 种形式：ARTⅠ 型处理双极型或二进制信号； ART Ⅱ 型是 ART Ⅰ的扩展形式， 用于处理连续型模拟信号；ART Ⅲ 型是分级搜索模型，兼容前两种结构的功能并将两层神经元网络扩大为任意多层神经元网络 。由于 ART Ⅲ 型在神经元的运行模型中纳入了生物神经元的生物电化学反应机制， 因而具备了很强的功能和可扩展能力。本文介绍ART I网络的工作原理，最后给出一个简单的例子以及相应的程序。

1. 灾难性遗忘问题

对于有导师信号的学习网络，通过反复输入样本模式达到稳定记忆，如果再加入新的样本继续训练，前面的训练结果就会逐渐受到影响。具体表现为对旧数据、旧知识的遗忘。无导师学习网络的权值调整式中都包含了对数据的学习项和对旧数据的忘却项，通过控制其中学习系数和忘却系数的大小达到某种折中。但这个系数的确定却没有一般的方法进行指导。所以，这两类神经网络的学习都会出现忘却旧样本的情况，导致网络分类性能受到影响。通过无限扩大网络规模解决样本遗忘是不现实的。
保证在适当增加网络规模的同时，在过去记忆的模式和新输入的训练模式之间作出某种折中，最大限度地接收新知识（灵活性）的同时保证较少的影响过去的模式样本（稳定性），ART网络较好地解决了这一问题。

ART网络及算法在适应新输入模式方面具有较大的灵活性，同时能够避免对先前所学模式的修改。
ART网络的思路是当网络接收新的输入时，按照预设定的参考门限检查该输入模式与所有存储模式类典型向量之间的匹配程度以确定相似度，对相似度超过门限的所有模式类，选择最相似的作为该模式的代表类，并调整与该类别相关的权值，以使后续与该模式相似的输入再与该模式匹配时能够得到更大的相似度。若相似度都不超过门限，就在网络中新建一个模式类，同时建立与该模式类相连的权值，用于代表和存储该模式以及后来输入的所有同类模式。

2. ART I型网络

按照神经网络的三元素：神经元模型、网络结构以及学习算法，进行介绍。

2.1 网络结构

2.1.1 网络系统结构如下图所示：

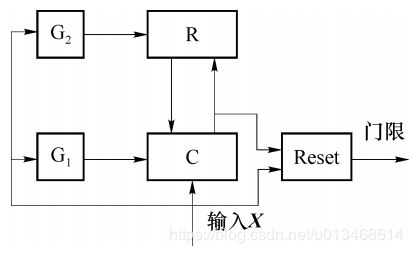
ART I网络结构由两层神经元构成两个子系统，分别为比较层C和识别层R，包含3种控制信号：复位信号R、逻辑控制信号G1和G2。

2.1.2 C层结构如下图所示：

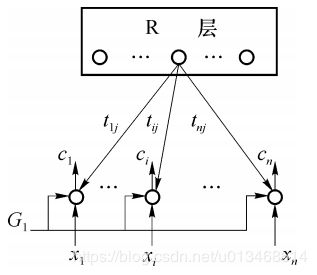
该层有n个神经元，每个接收来自3个方面的信号：外界输入信号，R层获胜神经元的外星权向量的返回信号和控制信号$G_1$。C层神经元的输出是根据2/3的多数表决原则产生，输出值与三个信号中的多数信号值相同。
网络开始运行时，$G_1=1$，识别层尚未产生竞争获胜神经元，因此反馈信号为0。由2/3规则，C层输出应取决于输入信号，有$C=X$。当网络识别层出现反馈回送信号时，$G_1=0$，由2/3规则，C层输出取决于输入信号与反馈信号的比较结果，如果xi = tij，则，$c_i=x_i$，否则$c_i=0$。可以看出控制信号$G_1$的作用是使得比较层能够区分网络运行的不同阶段，网络开始运行阶段$G_1$的作用是使得C层对输入信号直接输出，之后$G_1$的作用是使C层行使比较功能，此时$c_i$为$x_i$和$t_{ij}$的比较信号，两者同时为1，则$c_i$为1，否则为0。可以看出R层反馈信号对C层输出有调节作用。

2.1.3 R层结构如下图所示：

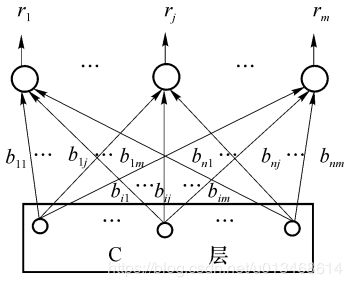
功能相当于前馈竞争网，R层有m个神经元，代表m个输入模式类，m可以动态增长，以设立新的模式类。C层的输出向量C沿着R层神经元的内星权向量到达R层神经元，经过竞争在产生获胜神经元处指示本次输入模式的所属类别。获胜神经元输出为1，其余为0。R层每个神经元都对应着两个权向量，一个是将C层前馈信号汇聚到R层的内星权向量，另一个是将R层反馈信号散发到C层的外星权向量。

2.1.4 控制信号

信号$G_2$检测输入模式$X$是否为0，它等于X各分量的逻辑或，如果xi全为0，则G2=0，否则G2=1。R层输出向量各分量的逻辑或为$R_0$，则信号$G_1=G_2$与（$R_0$的非）。当R层输出向量的各分量全为0而输入向量$X$不是0向量时，$G_1$为1，否则$G_1$为0。$G_1$的作用就是使得比较层能够区分网络运行的不同阶段，网络开始运行阶段G1的作用是使得C层对输入信号直接输出，之后$G_1$的作用是使C层行使比较功能，此时ci为xi和tij的比较信号，两者同时为1，则$c_i$为1，否则为0。Reset信号的作用是使得R层竞争获胜神经元无效，如果根据某种事先设定的测量标准，$T_j$与$X$未达到设定的相似度，表明两者未充分接近，于是系统发出Reset信号，使得竞争获胜神经元无效。

2.2 网络运行原理

网络运行时接受来自环境的输入模式，检查输入模式与R层所有已存储模式类之间的匹配程度。R层所存储的模式类是通过对应R层神经元的外星权向量体现出来的，对于匹配程度最高的获胜神经元，网络要继续考察其存储模式类与当前输入模式的相似程度。相似程度按照预先设计的参考门限来考察，可能出现如下的情况：
A. 如果相似度超过参考门限，将当前输入模式归为该类，全职调整规则是相似度超过参考门限的神经元调整其相应的内外星权向量，以使得以后遇到与当前输入模式接近的样本时能够得到更大的相似度；其他权向量则不做改动。
B. 如果相似度不超过门限值，则对R层匹配程度次高的神经元代表的模式类进行相似度的考察，若超过门限，网络的运行回到情况A，否则仍然回到情况B。如果最终存储的所有模式类与当前输入模式的相似度都没有超过门限，此时需在网络输出端设立一个代表新模式类的神经元，用以代表及存储该模式，以便参加以后的匹配过程。网络对所接受的每个新输入样本，都进行上面的运行过程。对于每个输入模式，网络运行过程可归纳为4个阶段：

2.2.1 匹配阶段

网络在没有输入模式之前处于等待状态，此时输入端$X=0$。当输入不全为0的模式$X$时，$G_1=1$允许输入模式直接从C层通过，并前向传至R层，与R层神经元对应的所有内星权向量$B_j$进行匹配计算：$$ne{t}_j=B_j^{T}X=\sum _{i=1}^n{b}_{ij}{x}_i$$
选择具有最大匹配度（具有最大点积）的竞争获胜神经元：$$ne{t}_j^{\ast }=\underset{j}{\max }\{ne{t}_j\}$$
使获胜神经元输出$r_j^{\ast }=1$，其他神经元输出为0.

2.2.2 比较阶段

使得Ｒ层获胜神经元所连接的外星权向量$T_j^{\ast }$激活，从神经元ｊ发出的ｎ个权值信号返回到Ｃ层的ｎ个神经元。此时，Ｒ层输出不全为零，则Ｃ层最新的输出状态取决于Ｒ层返回的外星权向量与网络输入模式Ｘ的比较结果。由于外星权向量是Ｒ层模式类的典型向量，该比较结果反映了在匹配阶段Ｒ层竞争排名第一的模式类的典型向量与当前输入模式Ｘ的相似度。相似度的大小可用相似度${Ｎ}_0$反应，定义为：$$N_0=X^T{t}_j^{\ast }=\sum _{i=1}^n{t}_{ij}^{\ast }{x}_i=\sum _{i=1}^n{c}_i$$
因为输入$x_i$为二进制数，$N_0$实际上表示获胜神经元的类别模式典型向量与输入模式样本相同分量同时为1的次数。输入模式样本中的非0分量数位$N_1$ $$N_1=\sum _i^n{x}_i$$
用于比较警戒门限为$\rho$，在$01$之间取值，检查输入模式与模式类典型向量之间的相似度是否低于警戒门限，如果有：
$$N_0/N_1<\rho$$
则$X$与$T_j^{\ast }$的相似度不满足要求，网络发出Reset信号，使得第一阶段的匹配失败，竞争获胜神经元无效，网络进入搜索阶段。如果有$$N_0/N_1>\rho$$
表明$X$与获胜神经元对应的类别模式非常接近，称$X$与$T_j^{\ast }$发生共振，第一阶段匹配结果有效，网络进入学习阶段。

2.2.3 搜索阶段

网络发出Reset重置信号后即进入搜索阶段，重置信号的作用是使前面通过竞争获胜的神经元受到抑制，并且在后续过程中受到持续的抑制，直到输入下一个新的模式为止。由于R层中竞争获胜的神经元被抑制，从而再度出现$R_0=0$,$G_1=1$,因此网络又重新回到起始的匹配状态。由于上次获胜的神经元持续受到抑制，此次获胜的必然是上次匹配程度排第二的神经元。然后进入比较阶段，将该神经元对应的外星权向量$t_j^{\ast }$ 与输入模式进行相似度计算。如果所有R层的模式类，在比较阶段相似度检查中相似度都不能满足要求，说明当前输入模式无类可归，需要在网络输出层增加一个神经元来代表并存储该模式类，为此将其内星权向量$B_j^{\ast }$设计为当前输入模式向量，外星权向量$T_j^{\ast }$各分量全设置为1。

2.2.4 学习阶段

在学习阶段要对发生共振的获胜神经元对应的模式类加强学习，使以后出现与该模式相似的输入样本时能获得更大的共振。
外星权向量$T_j^{\ast }$ 和内星权向量$B_j^{\ast }$ 在运行阶段进行调整以进一步强化记忆。经过学习后，对样本的记忆将留在两组权向量中，即使输入样本改变，权值依然存在，因此称为长期记忆。当以后输入的样本类似已经记忆的样本时，这两组长期记忆将R层输出回忆至记忆样本的状态。

2.3 网络学习算法

ART I网络可以用学习算法实现，也可以使用硬件实现。训练可以按照以下步骤进行：
(1) 网络初始化
从C层上行到R层，内星权向量$B_j$赋予相同的较小数值，如$$b_{ij}(0)=\frac{1}{1+n}$$
从R层到C层的外星权向量$T_j$各分量均赋值为1
初始权值对整个算法影响重大，内星权向量按照上式进行设置，可保证输入向量能够收敛到其应属类别而不会轻易动用未使用的神经元。外星权向量各分量设置为1可保证对模式进行相似性测量时能正确计算其相似性。
相似性测量的警戒门限ρ 设置为0~1之间的数，表示两个模式相近多少才被认为是相似的，因此其大小直接影响分类精度。
(2)网络接受输入
给定一个输入模式，$X=(x_1,x_2,...,x_n),x_i\in (0,1{)}^n$
(3)匹配度计算
对R层所有内星权向量$B_j$ 计算输入模式$X$的匹配度： $$B_j^{T}X=\sum _{i=1}^n{b}_{ij}{x}_i$$
(4)选择最佳匹配神经元
在R层有效输出神经元集合$J^{\ast }$内选择竞争获胜的最佳匹配神经元$j^{\ast }$，使得
$$r_j^{\ast }=1,else,r_j=0$$
(5)相似度计算
R层获胜神经元j∗ 通过外星送回存储模式类的典型向量T∗j ，C层输出信号给出对向量$T_j^{\ast }$ 和X的比较结果$c_i=t_{ij}^{\ast }$ ，由此结果可计算出两向量的相似度为：$$N_1=\sum _1^n{x}_i,N_0=\sum _1^n{c}_i$$
(6)警戒门限检验
按照设定的门限$\rho$ 进行相似度检验。
(7)搜索匹配模式类
按照上面介绍的方法进行模式类搜索。
(8)调整网络权值
修改R层神经元$j^{\ast }$对应的权向量，网络学习采用两种规则，外星权向量调整按照以下规则：
$$t_{ij}^{\ast }(t+1)=t_{ij}^{\ast }{x}_i$$
外星权向量为对应模式类的典型向量或称聚类中心，内星权向量的调整按照以下规则：
$$b_{ij}^{\ast }(t+1)=\frac{t_{ij}^{\ast }(t)x_i}{0.5+{\sum }_{i=1}^n{t}_{ij}^{\ast }(t)x_i}=\frac{t_{ij}^{\ast }(t+1)}{0.5+{\sum }_{i=1}^n{t}_{ij}^{\ast }(t+1)}$$
可以看出，如果不计分母中的常数0.5，上式相当于对外星权向量归一化。

2.4 ART I示例程序

"""
ART1 神经网络练习
author Toby
"""
import numpy as np

def ART_learn(train_data_active, weight_t_active, weight_b_active, n):
    weight_t_update =  train_data_active * weight_t_active
    weight_b_update = weight_t_update / (0.5 + np.sum(weight_t_update))
    return weight_t_update, weight_b_update

def ART_core(train_data, R_node_num, weight_b, weight_t, threshold_ro, n):
    data_length, data_num = train_data.shape
    result= np.zeros(data_num)
    for i in range(data_num):
        R_node = np.zeros(R_node_num)
        for n in range(R_node_num):
            net = []
            for j in range(R_node_num):
                net.append(np.sum(np.dot(train_data[:,i], weight_b[:,j])))
            j_max = np.where(net == np.max(net))[0][0]
            if R_node[j_max] == 1:
                net[j_max] = -n
            j_max = np.where(net == np.max(net))[0][0]
            R_node[j_max] = 1
            
            weight_t_active = weight_t[:, j_max]
            weight_b_active = weight_b[:, j_max]
            Similarity_N0 = np.sum(weight_t_active*train_data[:,i])
            Similarity_N1 = np.sum(train_data[:,1])
            flag = 1
            if threshold_ro < Similarity_N0 / Similarity_N1:
                weight_t[:,j_max], weight_b[:,j_max] = ART_learn(train_data[:,i], weight_t_active, weight_b_active, j_max)
                print('样本%d属于第%d类\n'%(i, j_max))
                result[i] = j_max                
                flag = 0
                break
            
        if flag == 1:
            R_node_num = R_node_num + 1
            if R_node_num == data_num + 1:
                print('样本%d属于第%d类\n 错误: 目前的分类类别数为%d \n'%(i, R_node_num, R_node_num))
                return R_node_num,weight_b,weight_t,result
            weight_b = np.column_stack((weight_b, train_data[:,i]))
            weight_t = np.column_stack((weight_t, np.ones(data_length)))
            print('样本%d属于第%d类\n'%(i, R_node_num))
            result[i] = R_node_num
    return R_node_num,weight_b,weight_t,result
            
            
            
train_data=np.array([[0,0,0,1,1,1,0],
                    [0,0,0,1,1,0,0], 
                    [0,0,0,1,0,1,1],  
                    [1,0,1,0,1,0,1], 
                    [1,1,1,0,1,0,0],  
                    [1,1,0,0,0,0,1]])
data_length, data_num = train_data.shape
N = 100
R_node_num = 3
weight_b = np.ones([data_length, R_node_num]) / N
weight_t = np.ones([data_length, R_node_num])
threshold_ro = 0.5
result_pre = np.zeros(data_num)
IsOver = False
for n in range(10):
    R_node_num, weight_b, weight_t, result = ART_core(train_data, R_node_num, weight_b, weight_t, threshold_ro,n)
    for i in range(min(len(result), len(result_pre))):
        IsOver = True
        if result[i] != result_pre[i]:
            IsOver = False
            break
    if IsOver:
        print('样本分类迭代完成！！！！')
        break
    if R_node_num == data_num+1:
        print('分类错误：样本类别数大于样本数')
    print("------------------------")
    result_pre = result

输出结果：
样本0属于第0类

样本1属于第0类

样本2属于第1类

样本3属于第2类

样本4属于第1类

样本5属于第2类

样本6属于第4类

---

样本0属于第3类

样本1属于第0类

样本2属于第1类

样本3属于第2类

样本4属于第1类

样本5属于第2类

样本6属于第3类

---

样本0属于第0类

样本1属于第0类

样本2属于第1类

样本3属于第2类

样本4属于第1类

样本5属于第2类

样本6属于第3类

---

样本0属于第0类

样本1属于第0类

样本2属于第1类

样本3属于第2类

样本4属于第1类

样本5属于第2类

样本6属于第3类

样本分类迭代完成！！！！

3 . 总结

ART网络的特点是非离线学习，即不是对输入样本反复训练后才开始运行，而是边学习边运行的实时方式，每个输出神经元可以看做一类相近样本的代表，每次最多只有一个输出神经元1。当输入样本距离某一个内星权向量较近时，代表它输出神经元才响应，通过调整警戒门限的大小，可调整模式的类数，ρ小，模式的类别少，ρ大，则模式的类别多。
用硬件实现ART I模型时，C层和R层的神经元都用电路实现，作为长期记忆的权值用CMOS电路完成。