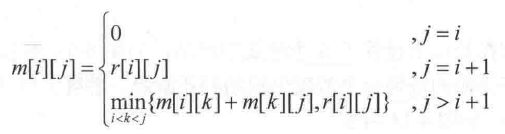趣学算法(4)——动态规划

目录

4.3 最长的公共子序列

问题描述：

问题分析:

算法实现：

4.4 编辑距离

问题分析:

算法思想:

算法实现:

4.5 游船租赁

问题描述:

问题分析:

算法实现:

4.6 矩阵连乘

问题描述:

问题分析：

算法思想:

算法实现:

---

动态规划是一种分治思想，但与分治算法不同的是，分治算法是把原问题分解为若干子问题，自顶向下求解各种子问题，合并子问题的解，从而得到原问题的解。动态规划也是把原问题分解为若干子问题，然后自底向上，先求解最小的子问题，把结果存储在表格中，再求解大的子问题时，直接从表格中查询小的子问题的解，避免重复计算，从而提高算法效率。

什么问题可以使用动态规划呢？首先要分析问题是否具有以下两个性质：

(1)最优子结构

最优子结构性质是指问题的最优解包含其子问题的最优解。最优子结构是使用动态规划的最基本条件，如果不具有最优子结构性质，就不可以使用动态规划解决。

(2)子问题重叠

子问题重叠是指在求解子问题的过程时，有大量的子问题是重复的，那么只需要求解一次，然后把结果存储在表中，以后使用时可以直接查询，不需要再次求解。子问题重叠不是使用动态规划的必要条件，但问题存在子问题重叠更能够充分彰显动态规划的优势。

遇到一个实际问题，如何采用动态规划来解决呢？

(1)分析最优解的结构特征。

(2)建立最优值的递归式。

(3)自底向上计算最优值，并记录。

(4)构造最优解。

4.3 最长的公共子序列

问题描述：

指定两个序列X = {x1, x2, x3, …, xm}和Y = {y1, y2, y3, …, yn}, 找出X和Y的一个最长的公共子序列。

问题分析:

最长公共子序列长度递归式：

算法实现：

"""

最长公共子序列

"""


class LCS():
    def __init__(self, s1, s2):
        self.s1 = s1
        self.s2 = s2
        self.c = [[0 for i in range(len(self.s2)+1)] for j in range(len(self.s1)+1)]  # 记录最长子序列的长度
        self.b = [[0 for i in range(len(self.s2)+1)] for j in range(len(self.s1)+1)]  # 记录来源
        self.code = []  # 存储最长公共子序列

    def getLCS(self):
        self.s1 = '0' + self.s1
        self.s2 = '0' + self.s2
        for i in range(1, len(self.s1)):
            for j in range(1, len(self.s2)):
                if self.s1[i] == self.s2[j]:
                    self.c[i][j] = self.c[i-1][j-1] + 1
                    self.b[i][j] = 1  # 当前位置处于最长序列中
                else:
                    if self.c[i-1][j] > self.c[i][j-1]:
                        self.c[i][j] = self.c[i-1][j]
                        self.b[i][j] = 2  # 来源于上方
                    else:
                        self.c[i][j] = self.c[i][j-1]
                        self.b[i][j] = 3  # 来源于左方

    def getch(self):
        i = len(self.s1) - 1
        j = len(self.s2) - 1
        while i > 0 and j > 0:
            if self.b[i][j] == 1:
                self.code.append(self.s1[i])
                i -= 1
                j -= 1
            elif self.b[i][j] == 2:
                i -= 1
            else:
                j -= 1
        self.code.reverse()


test = LCS('ABCADAB', 'BACDBA')
test.getLCS()
test.getch()
print(test.code)

4.4 编辑距离

问题分析:

编辑距离是指将一个字符串替换为另一个字符串所需要的最小编辑操作。

算法思想:

编辑距离递归式：

d[i][j] = min{d[i-1][j]+1, d[i][j-1]+1, d[i-1][j-1]+diff[i][j]}

算法实现:

"""

编辑距离

"""


def editdistance(s1, s2):
    s1 = '0'+s1
    s2 = '0'+s2
    c = [[0 for j in range(len(s2))] for i in range(len(s1))]
    for i in range(len(s2)):
        c[0][i] = i
    for i in range(len(s1)):
        c[i][0] = i
    for i in range(1, len(s1)):
        for j in range(1, len(s2)):
            if s1[i] == s2[j]:
                diff = 0
            else:
                diff = 1
            c[i][j] = min(c[i][j-1]+1, c[i-1][j]+1, c[i-1][j-1]+diff)
    # print(c[len(s1) - 1][len(s2) -1])
    i = len(s1) - 1
    j = len(s2) - 1
    while i > 0 and j > 0:  # 这里需要在琢磨下
            if s1[i] == s2[j]:
                diff = 0
            else:
                diff = 1
            if c[i][j] == c[i-1][j-1] + diff:
                if diff == 1:
                    print("%c 替换为 %c"%(s1[i], s2[j]))
                i -= 1
                j -= 1
            elif c[i][j] == c[i][j-1] + 1:
                print('在%d后插入%c'%(i, s2[j]))
                j -= 1
            else:
                print('删除%c'%s1[i])
                i -= 1

editdistance("family", 'frame')

4.5 游船租赁

问题描述:

长江游艇俱乐部在长江上设置了n个游艇出租站，游客可以在这些游艇出租站租用游艇，并在下游的任何一个游艇出租站归还游艇。游艇出租站i到游艇出租站j之间的租金为r(i,  j), 1 <= i

问题分析:

分析第i个站点到第j个站点(i, i+1, .., j)的最优解(最少租金)问题，考察是否具有最优子结构性质。

(1)分析最优解的结构特征

假设我们已经知道了在第k个站点停靠会得到最优解，那么原问题就变成了两个子问题: (i, i+1, …, k)、(k, k+1, …, j)。

那么原问题的最优解是否包含子问题的最优解呢？

假设第i个站点到第j个站点(i, i+1, …, j)的最优解是c， 子问题(i, i+1, …, k)的最优解是a，子问题(k, k+1, …, j)的最优解是b，那么c=a+b，无论两个子问题的停靠策略如何都不影响它们的结果，因此我们只需要证明如果c是最优的，则a和b一定是最优的(即原问题的最优解包含子问题的最优解)。（结果显而易见）

(2)建立最优值的递归式

用m[i][j]表示第i个站点到第j个站点(i, i+1, …, j)的最优值(最少租金)，那么两个子问题: (i, i+1, …, k)、(k, k+1, …, j)对应的最优值分别是m[i][k]、m[k][j]。

游艇租金最优值递归式:

当j=i时，只有1个站点，m[i][j] = 0

当j=i+1时，只有2个站点，m[i][j] = r[i][j]

当j>i+1时，有3个以上站点，m[i][j] = min{m[i][k]+m[k][j], r[i][j]}。

整理如下:

(3)自底向上计算最优值，并记录

先求两个站点之间的最优值，再求第3个站点之间的最优值，直到n个站点之间的最优值。

(4)构造最优解

上面得到的最优值只是第1个站点到第n个站点之间的最少租金，并不知道停靠了哪些站点，我们需要从记录表中还原，逆向构造出最优解。

算法实现:

"""

游船租赁:
长江游艇俱乐部在长江上设置了n个游艇出租站，游客可以在这些游艇出租站租用游艇，并在下游的任何一个游艇出租站归还游艇。
游艇出租站i到游艇出租站j之间的租金为r(i,  j), 1 <= i

4.6 矩阵连乘

问题描述:

对于给定n个连乘的矩阵，找出一种加括号的方法，使得矩阵连乘的计算量(乘法次数)最小。

问题分析：

研究矩阵连乘问题是否具有最优子结构性质。(类比游船租赁问题)

算法思想:

(1)建立最优值递归式：

当i=j时，只有一个矩阵， m[i][j] = 0;

当i>j时，m[i][j] = min{m[i][k]+m[k+1][j]+PiPk+1Qj}

用一维数组p[]记录矩阵的行和列，第i个矩阵的行数存储在数据的第i-1位置，列数存储在数组的第i位置，那么PiPk+1Qj对应的数组元素相乘为p[i-1]p[k]p[j]

(2)自底向上计算并记录最优值

先求两个矩阵相乘的最优值，再求3个矩阵相乘的最优值，直到n个矩阵连乘的最优值。

(3)构造最优解

上面得到的最优值只是矩阵连乘的最小的乘法次数，并不知道加括号的次序，需要从记录表中还原加括号次序，构造出最优解，例如A1(A2A3)

这个问题是一个动态规划求解矩阵连乘最小计算量的问题，将问题分为小规模的问题，自底向上计算，将规模放大，直到得到所求规模的问题的解。

算法实现:

"""

矩阵连乘 (和游船租赁问题有点类似)

"""


total = int(input())  # 矩阵个数
p = list(map(int, input("输入每个矩阵的行数和最后一个矩阵的列数").split()))
m = [[0 for j in range(total + 1)] for i in range(total+1)]
s = [[0 for j in range(total + 1)] for i in range(total+1)]


def rect_mul():
    d = 2
    while d <= total:  # 逐步缩小问题规模，先考虑两两矩阵，在考虑3个矩阵，最后考虑total个矩阵
        for i in range(1, total-d+1+1):
            j = i+d-1
            m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j]  # 默认i,j以i为中间计算节点
            s[i][j] = i  # 记录分割点
            for k in range(i+1, j):
                if m[i][j] > m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]:
                    m[i][j] = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]
                    s[i][j] = k
        d += 1


def print_path(start, end):
    if start == end:
        print("A[%d]" % start, end='')
    else:
        print("(", end='')
        print_path(start, s[start][end])
        print_path(s[start][end]+1, end)
        print(")", end='')


rect_mul()
print_path(1, total)