第2章 数据
本章讨论一些与数据相关的问题,对于数据挖掘的成本至关重要。
数据类型 数据集的不同表现在很多方面。例如,用来描述数据对象的属性可以具有不同的类型---定量的或定性的,并且数据集可能具有特定的性质,例如,某些数据集包含时间序列或彼此之间具有明显联系的对象。毫不奇怪,数据的类型决定我们应使用何种工具和技术来分析数据。此外,数据挖掘研究常常是为了适应新的应用领域和新的数据类型的需要而展开的。
数据的质量 数据通常远非完美。尽管大部分数据挖掘技术可以忍受某种程度的数据不完美,但是注重理解和提高数据质量将改进分析结果的质量。通常必须解决的数据质量问题包括存在噪声和离群点,数据遗漏、不一致或重复,数据有偏差或者不能代表它应该描述的现象或总体情况。
使数据适合挖掘的预处理步骤 原始数据必须加以处理才能适合于分析。处理一方面是要提高数据的质量,另一方面要让数据更好地适应特定的数据挖掘技术或工具。例如,可能需要将连续值属性(如长度)转换成具有离散的分类纸的属性(如短、中、长),以便应用特定的技术。又如,数据集属性的数目常常需要减少,因为属性较少时许多技术用起来更加有效。
根据数据联系分析数据 数据分析的一种方法时找出数据对象之间的联系,之后使用这些联系而不是数据对象本身来进行其余的分析。例如,我们可以计算对象之间的相似度或距离,然后根据这种相似度或距离进行分析---聚类、分类或异常检测。诸如此类的相似性或距离度量很多,要根据数据的类型和特定的应用做出正确的选择。
例2.1 与数据相关的问题。这个场景代表一种极端情况,但它强调“了解数据”的重要。为此,本章将处理上面提到的四个问题,列举一些基本难点和标准解决方法。
2.1 数据类型
通常,数据集可以看做数据对象的集合。数据对象有时也叫做记录、点、向量、模式、时间、案例、样本、观测或实体。数据对象用一组刻画对象基本特性的属性描述。属性有时也叫做变量、特性、字段、特征或维。
例2.2 学生信息 通常,数据集是一个文件,其中对象是文件的记录,而每个字段对应于一个属性。例如,下表显示包含学生信息的数据集,每行对应于一个学生,而每列是一个属性,描述学生的某一方面,如平均成绩或标志号。
基于记录的数据集在平展文件或关系数据库系统中是最常见的,但是还有其他类型的数据集和存储数据的系统。
2.1.1 属性和度量
本节考虑使用何种类型的属性描述数据对象,来处理描述数据的问题。首先定义属性,然后考虑属性类型的含义,最后介绍经常遇到的属性类型。
1. 什么是属性
定义2.1 属性(attribute)是对象的性质或特性,它因对象而异,或随时间而变化。
例如,眼球颜色因人而异,而物体的温度随时间而变。注意:眼球颜色是一种符号属性,具有少量可能的值(棕色、黑色、蓝色、绿色、淡褐色,......),而温度是数值属性,可以取无穷多个值。
追根溯源,属性并非数字或符号。然而,为了讨论和惊喜地分析对象的特性,我们为它们赋予了数字或符号。为了用一种明确定义的方式做到这一点,我们需要测量标度。
定义2.2 测量标度(measurement scale)是将数值或符号值与对象的属性相关联的规则(函数)。
形式上,测量过程是使用测量标度将一个值与一个特定对象的特性属性相关联。这看上去有点抽象,然是任何时候,我们总在进行这样的测量过程。例如,踏上磅秤称体重;将人分为男女;清点会议室的椅子数目,确定是否能够为所有与会者提供足够的座位。在所有这些情况下,对象属性的“物理值”都被映射到数值或符号值。
有了这些背景,现在我们可以讨论属性类型,这对于确定特定的数据分析技术是否适用于某种具体的属性是一个重要的概念。
2. 属性类型
属性的性质不必与用来度量它的值的性质相同。换句话说,用来代表属性的值可能具有不同于属性本身的性质,并且反之亦然。
例2.3 雇员年龄和ID号 与雇员有关的两个属性是ID和年龄。这两个属性都可以用整数表示。然而,谈论雇员的平均年龄是有意义的,但是谈论雇员的平均ID却毫无意义。我们希望ID属性所表达的唯一方面是它们互不相同。因而,对雇员ID的唯一合法操作就是判定它们是否相等。但在使用证书表示雇员ID时,并没有暗示此限制。对于年龄属性而言,用来表示年龄的整数的性质与该属性的性质大同小异。尽管如此,这种对应仍不完备,例如,年龄有最大值,而整数没有。
例2.4 线段长度 考虑下图,它展示一些线段对象和如何用两种不同的方法将这些对象的长度属性映射到整数。
属性的类型告诉我们,属性的哪些性质反映在用于测量它的值中。知道属性的类型是重要的,因为它告诉嗯测量值的哪些性质与属性的基本性质一致,从而使得我们可以避免诸如计算雇员的平均ID这样的愚蠢行为。注意,通常将属性的类型称做测量标度的类型。
3. 属性的不同类型
一种制定属性类型的有用的办法是,确定对应于属性基本性质的数值的性质。例如,长度的属性可以有数值的许多性质。按照长度的比较对象,确定对象的排序,以及谈论长度的差和比例都是有意义的。数值的如下性质常常用来描述属性。
(1)相异性 =和≠
(2)序>\<\≥和≤
(3)加减法 +和-
(4)乘除法 *和/
给定这些性质,可以定义四种属性类型:标称、序数、区间和比率。下表给出这些类型的定义,以及每种类型上有哪些合法的统计操作等信息。每种属性类型拥有其上方属性类型上的所有性质和操作。因此,对于标称、序数和区间属性合法的任何性质或操作,对于比率属性也合法。
标称和序数属性统称分类的(categorical)或定性的(qualitative)属性。顾名思义,定性属性不具有数的大部分性质。即便使用数(即整数)表示,也应当像对待符号一样对待他们。其余两种类型的属性,即区间和比率属性,通常定量的(quantitative)或数值的(numeric)属性。定量属性用数表示,并且具有数的大部分性质。注意,定量属性可以使整数值或连续值。
属性的类型也可以用不改变属性意义的变换来描述。
对特定的属性类型有意义的统计操作是这样一些操作。当使用保持属性意义的变换对属性进行变换时,它们产生的结果相同。
例2.5 温度标度 温度可以很好地解释前面介绍的一些概念。首先,温度可以使区间属性或比率属性,这取决于其测量标度。当温度用绝对标度测量时,从物理意义上讲,2°的温度是1°的两倍;当温度用华氏或摄氏度标度测量时则并非如此。因为这时1°温度与2°温度相差并不太多。
4. 用值得个数描述属性
区分属性的一种独立方法时根据属性可能取值的个数来判断。
离散的(discrete)离散属性具有有限个值或无限可数个值。这样的属性可以使分类的,如邮政编码或ID号,也可以是数值的,如计数。通常,离散属性用整数变量表示。二元属性(binary attribute)是离散属性的一种特殊情况,并只接受两个值,如真假、是否、男女或01。通常,二元属性用布尔变量表示,或者用只取两个值0或1的整型变量表示。
连续的(continuous)连续属性是取实数值的属性。如温度、高度或重量等属性。通常,连续属性用浮点变量表示。实践中,实数值只能用有限的精度测量和表示。
从理论上讲,任何测量标度类型都可以与基于属性值个数的任意类型组合。然后,有些组合并不常出现,或者没有什么意义。
5. 非对称的属性
对于非对称的属性,出现非零属性值才是重要的。考虑这样一个数据集,其中每个对象是一个学生。而每个属性记录学生是否选修大学的某个课程。对于某个学生,如果他选修了对应于某属性的课程,则该属性取值1,否则取值0。由于学生只选修所有可选课程中的一小部分,这种数据集的大部分值为0。因此,关注非零值将更有意义、更有效。否则,如果在学生们不选修的课程上做比较,则大部分学生都非常相似。只有非零值才重要的二元属性是非对称的二元属性。这类属性对于关联分析特别重要。
2.1.2 数据集的类型
数据集的类型有多种,并且随着数据挖掘的发展和成熟,还会有更多类型的数据集将用于分析。本节介绍一些很常见的类型。为方便起见,将数据集类型分成三组:记录数据、基于图形的数据和有序的数据。这些分类不能涵盖所有的可能性,肯定还存在其他的分组。
1. 数据集的一般特性
在提供特定类型数据集的细节之前,先讨论适用于许多数据挖掘的三个特性,它们对数据挖掘技术具有重要影响,它们是维度、稀疏性和分辨率。
维度(dimensionality)数据集的维度是数据集中的对象具有的属性数目。低维度数据往往与中、高维度数据有质的不同。确实,分析高维数据有时会陷入所谓维度灾难(curse of dimensionality)。正因为如此,数据预处理的一个重要动机就是减少维度,称为维归约(dimensionality reduction)。这些问题会在后面更深入地讨论。
稀疏性(sparsity)有些数据集,如具有非对称特征的数据集,一个对象的发部分属性上的值都为0;在许多情况下,非零项还不到1%。实际上,稀疏性是一个优点,因为只有非零值才需要存储和处理。这将节省大量的计算时间和存储空间。此外,有些数据挖掘算法仅适合处理稀疏数据。
分辨率(resolution)常常可以在不同的分辨率下得到数据,并且在不同的分辨率下数据的性质也不同。例如,在几米的分辨率下,地球表面看上去很不平坦,但在数十公司的分辨率下去相对平坦。数据的模式也依赖于分辨率,如果分辨率太高,模式可能看不出,或者掩埋在噪声中;如果分辨率太低,模式可能不出现。例如,几小时记录一下气压变化可以反映出风暴等天气系统的移动;而在月的标度下,这些现象就检测不到。
2. 记录数据
许多数据挖掘任务都假定数据集是记录(数据对象)的汇总,每个记录包含固定的数据字段(属性)集。如下图,对于记录数据的大部分基本形式,记录之间或数据字段之间没有明显的联系,并且每个记录(对象)具有相同的属性集。记录数据通常存放在平展文件或关系数据库中。关系数据库当然不仅仅是记录的汇集,它还包含更多的信息。但是数据挖掘一般并不适用关系数据库的这些信息。更确切的说,数据库是查找记录的方便场所。下面介绍不同类型的记录数据,如下图所示:
事务数据或购物篮数据 事务数据(transaction data)是一种特殊类型的记录数据,其中每个记录(事务)涉及一系列的项。考虑一个杂货店。顾客一次购物所购买的商品的集合就构成一个事务,而购买的商品是项。这种类型的数据称作购物篮数据(market basket data),因为记录中的项是顾客“购物篮”中的商品。事务数据时项的集合的集族,但是也能将它视为记录的集合,其中记录的字段是非对称的属性。这些属性常常是二元的,指出商品是否已购买。更一般地,这些属性还可以是离散的或连续的,例如表示购买的商品数量或购买商品的花费。图(b)展示了一个事务数据集,每一行代表一位顾客在特定时间购买的商品。
数据矩阵 如果一个数据集族中的所有数据对象都具有相同的数值属性集,则数据对象可以看做多为空间中的点(向量),其中每个维代表对象的一个不同属性。这样的数据对象集可以用一个mxn的矩阵表示。其中m行,一个对象一行;n列,一个属性一列。这种矩阵称为数据矩阵(data matrix)或模式矩阵(pattern matrix)。数据矩阵是记录数据的变体,但是由于它由数值属性组成,可以使用标准的矩阵操作对数据进行变换和处理,因此,对于大部分统计数据,数据矩阵是一种标准的数据格式。图(c)展示出一个样本数据矩阵。
稀疏数据矩阵 稀疏数据矩阵是数据矩阵的一种特殊情况。其中属性的类型相同并且是非对称的,即只有非零值才是重要的。事务数据仅含0-1元素的稀疏数据矩阵的例子。另一个常见的例子是文档数据。特别地,如果忽略文档中词的次序,则文档可以用词向量表示,其中每个词是向量的一个分量(属性),而每个分量的值是对应词在文档中出现的次数。文档集合的这种表示通常称作文档-词矩阵(documen-term matrix)。图(d)展示了一个文档-词矩阵。文档是该矩阵的行,而词是矩阵的列。实践应用时,近存放稀疏数据矩阵的非零项。
3. 基于图形的数据
有时,图形可以方便而有效地表示数据。我们考虑两种特殊情况:(1)图形捕获数据对象之间的联系,(2)数据对象本身用图形表示。
带有对象之间联系的数据 对象之间的联系常常携带重要信息。在这种情况下,数据常常用图形表示。一般把数据对象映射到图的节点,而对象之间的联系用对象之间的链和诸如方向、权值等链性质表示。考虑万维网上的网页,页面上包含文本和指向其他页面的链接。为了处理搜索查询,web搜索引擎收集并处理网页,提取它们的内容。然而,众所周知,指向或出自每个页面的链接包含了大量该页面与查询相关程度的信息,因而必须考虑。下图显示了相互链接的网页集。
具有图形对象的数据 如果对象具有结构,即对象包含具有联系的子对象,则这样的对象常常用图形表示。例如,化合物的结构可以用图形表示,其中节点是原子,节点之间的链式化学键。如上图给出化合物苯的分子结构示意图,包含碳原子和氢原子。图形表示可以确定何种子结构频繁地出现在化合物的集合中,并且查明这些子结构中是否有某种子结构与诸如熔点或生成热等特定的化学性质有关。子结构挖掘是数据挖掘中分析这类数据的一个分支,将在7.5节讨论。
4. 有序数据
对于某些数据类型,属性具有涉及时间或空间序的联系。下面介绍各种类型的有序数据,并显示在下图中。
时序数据 时序数据(sequential data)也称时间数据(temporal data),可以看做记录数据的扩充,其中每个记录包含一个与之相关联的时间。考虑存储事务发生时间的零售事务数据。时间信息可以帮助我们发现“万圣节前夕糖果销售达到高峰”之类的模式。时间也可以与每个属性相关联。例如,每个记录可以是一位顾客的购物历史,包含不同时间购买的商品列表。使用这些信息,就有可能发现“购买DVD播放机的人趋向于在其后不久购买DVD”之类的模式。
图(a)展示了一些时序事务数据,有5个不同的时间---t1到t5;3位不同的顾客---c1到c3;5中不同的商品---A到E。在图上面的表中,每行对应于一位顾客在特定的时间购买的商品。下面的表显示相同的信息,但每行对应于一位顾客。每行包含涉及该顾客的所有事物信息,其中每个事物包含一些商品和购买这些商品的时间。
序列数据 序列数据(sequence data)是一个数据集合,它是各个实体的序列,如词或字母的序列。除没有时间戳之外,它于时序数据非常相似,只是有序序列考虑项的位置。例如,动植物的遗传信息可以用称作基因的核苷酸的序列表示。与遗传序列数据有关的许多问题都涉及由核苷酸序列的相似性预测基因结构和功能的相似性。图(b)展示了用4种核苷酸表示的一段人类基因码、所有DNA都可以用ATGC四种核苷酸构造。
时间序列数据 时间序列数据(time series data)是一种特殊的时序数据,其中每个记录都是一个时间序列(time series),即一段时间以来的测量序列。例如,金融数据集可能包含各种股票每日价格的时间序列对象。再例如,如图(c),该图显示明尼阿波利斯从1982年到1994年的月平均气温的时间序列。在分析时间数据时,重要的是要考虑时间自相关(temporal autocorrelation),即如果两个测量的时间很接近,则这些测量的值通常非常相似。
空间数据 有些对象除了其他类型的属性之外,还具有空间属性,如位置或区域。空间数据的一个例子是从不同的地理位置收集的气象数据。空间数据的一个重要特点是空间自相关性(spatial autocorrelation),即物理上靠近的对象趋向于在其他方面也相似。这样,地球上相互靠近的两个点通常具有相近的气温和降水量。
空间数据的红药例子是科学和工程数据集,其数据取自二维或三维网格上规则或不规则分布的点上的测量或模型输出。
5. 处理非记录数据
大部分数据挖掘算法都是为记录数据或其变体设计的。通过从数据对象中提取特征,并使用这些特征创建对应于每个对象的记录,针对记录数据的技术也可以用于非记录数据。考虑前面介绍的化学结构数据。给定一个常见的子结构集合,每个化合物都可以用一个具有二元属性的记录表示,这些二元属性指出化合物是否包含特定的子结构。这样的表示实际上是事务数据集,其中事务是化合物,而项是子结构。
在某些情况下,容易用记录形式表示数据,但是这类表示并不能捕获数据中的所有信息。考虑这样的时间空间数据,它由空间网格没一点上的时间序列组成。通常这种数据存放在数据矩阵中,其中每行代表一个位置,而每列代表一个特定的时间点。然而,这种表示并不能明确地表示属性之间存在的时间联系以及对象之间存在的空间联系。但并不是说这种表示不合适,而是说分析时必须考虑这些联系。例如,在使用数据挖掘技术时,假定属性之间在统计上是相互独立的并不是一个好主意。
2.2 数据质量
数据挖掘使用的数据常常是为其他用途收集的,或者在收集时未明确其目的。因此,数据挖掘常常不能“在数据源头控制质量”。相比之下,统计学的实验设计或调查往往其数据质量都达到了一定的要求。由于无法避免数据质量问题,因此数据挖掘着眼于两个方面:(1)数据质量问题的检测和纠正,(2)使用可以荣登低质量数据的算法。第一步的检测和纠正,通常称作数据清理(data cleaning)。
下面几节讨论数据质量,尽管也讨论某些与应用有关的问题,但是关注的焦点是测量和数据收集问题,
2.2.1 测量和数据收集问题
期望数据完美是不现实的。由于人的错误、测量设备的限制或数据收集过程的漏洞都可能导致问题。数据的值乃至这个数据对象都可能会丢失。在有些情况下,可能有不真实的或重复的对象,即对应于单个“实际”对象出现了多个数据对象。例如,对于一个最近住过两个不同地方的人,可能有两个不同的记录。即使所有的数据都不缺,并且“看上去很好”,也可能存在不一致,如一个人身高2m,但体重只有2kg。
在下面几节,关注数据测量和收集方面的数据质量问题。先定义测量误差和数据收集错误,然后考虑涉及测量误差的各种问题:噪声、伪像、偏倚、精度和准确率。最后讨论可能同时涉及测量和数据收集的数据质量问题:离群点、遗漏和不一致的值、重复数据。
1. 测量误差和数据收集错误
测量误差(measurement error)是指测量过程中导致的问题。一个常见的问题是:在某种程度上,记录的值与实际值不同。对于连续属性,测量值与实际值的差称为误差(error)。数据收集错误(data collection error)是指诸如遗漏数据对象或属性值,或不当地包含了其他数据对象等错误。例如,一种特定种类动物研究可能包含了相关种类的其他动物,它们只是表面上与要研究的种类相似。测量误差和数据收集错误可能是系统的也可能是随机的。
我们只考虑一般的错误类型。在特定的领域,总有些类型的错误是常见的,并且常常有很好的技术来检测并纠正这些错误。例如,人工输入数据时键盘录入错误是常见的,因此许多数据输入程序具有检测技术,并且通过人工干预纠正这类错误。
2. 噪声和伪像
噪声是测量误差的随机部分。这可能涉及值被扭曲或加入了谬误对象。下图显示被随机噪声干扰前后的时间序列。如果在时间序列上添加更多的噪声,形状将会消息。如下图显示了三组添加一些噪点前后的数据集。注意,有些噪点与非噪声点混在一起。
“噪声”通常用于包含时间或空间分量的数据。在这些情况下,常常可以使用信号或图像处理技术降低噪声,从而帮助发现可能“淹没在噪声中”的模式。尽管如此,完全消除噪声通常是困难的,而许多数据挖掘工作都关注设计鲁棒算法(robust algorithm),即在噪声干扰下也能产生可以接受的结果。
数据错误可能是更确定性现象的结果,如一组照片在同一地方出现条纹。数据的这种确定性失真常称为伪像(artifact)。
3. 精度、偏倚和准确率
在统计学和实验科学中,测量过程和结果数据的质量用精度和偏倚度量。给出标准的定义,随后简略加以讨论。对下面的定义,假定对相同的基本量进行重复测量,并使用测量值集合计算均值(平均值),作为实际值的估计。
定义2.3 精度(precision)(同一个量的)重复测量值之间的接近程度。
定义2.4 偏倚(bias) 测量值与被测量值之间的系统的变差。
精度通常用值集合的标准差度量,而偏倚用值集合的均值与测出的已知值之间的差度量。只有那些通过外部手段能够得到测量值的对象,偏倚才是可确定的。假定我们有1克质量的标准实验室种类,并且想评估实验室的新天平的精度和偏倚。我们称重5次,得到下列值:{1.015,0.990,1.013,1.001,0.986}。这些值得均值是1.001。因此偏倚是0.001.用标准差度量,精度是0.013。
通常使用更一般的术语准确率表示数据测量误差的程度。
定义2.5 准确率(accuracy) 被测量的测量值与实际值之间的接近度。
准确率依赖于精度和偏倚,但是由于它是一个一般化的概念,因此没有用这两个量表达准确率的公式。
准确率的一个重要方面是有效数字(significant digit)的使用,其目标是仅使用数据精度所能确定的数字位数表示测量或计算结果。例如,对象的长度用最小刻度为毫米的米尺测量,则我们只能记录最接近毫米的长度数据,这种测量的精度为±0.5mm。
诸如有效数字、精度、偏倚和准确率问题常常被忽略,但对于数据挖掘、统计学和自然科学,它们都非常重要。通常,数据集并不包含数据精度信息,用于分析的程序返回的结果也没有这方面的信息。但是,缺乏对数据和结果准确率的理解,分析者可能出现严重的数据分析错误。
4. 离群点
离群点(outlier)是在某种意义上具有不同于数据集中其他大部分数据对象的特征的数据对象,或是相对于该属性的典型值来说不寻常的属性值。我们也称其为异常(anomalous)对象或异常值。有许多定义离群点的方法,并且统计学和数据挖掘已经提出了很多不同的定义。此外,区别噪声和离群点这两个概念是非常重要的。离群点可以使合法的数据对象或值。因此,不像噪声,离群点本身有时是人们感兴趣的对象。例如,欺诈和网络攻击检测中,目标就是从大量正常对象或事件中发现不正常的对象和事件。第10章更详细地讨论异常检测。
5. 遗漏值
一个对象遗漏一个或多个属性的情况并不少见。有时可能会出现信息收集不全的情况。例如有的人拒绝透漏年龄或体重。还有些情况下,某些属性并不能用于所有对象,例如表格常常有条件选择部分,仅当填表人以特定的方式回答问题的时候,条件选择部分才需要填写。但为简单起见存储了表格的所有字段。无论何种情况,在数据分析时都应当考虑遗漏值。
有许多处理遗漏值的策略(和这些策略的变种),每种策略可能适用于特定的情况。这些策略在下面列出,同时我们指出它们的优缺点。
删除数据对象或属性 一种简单而有效的策略是删除具有遗漏值的数据对象。然而,即使不完整的数据对象也包含一些有用的信息,并且,如果许多对象都有遗漏值,则很难甚至不可能进行可靠的分析。尽管如此,如果某个数据集只有少量的对象具有遗漏值,则忽略它们可能是合算的。一种与之相关的策略是删除具有遗漏值的属性。然而,做这件事要小心,因为被删除的属性可能对分析是至关重要的。
估计遗漏值 有时,遗漏值可以可靠的估计。例如,在考虑以大致平滑的方式变化的、具有少量但分散的遗漏值的时间序列时,遗漏值可以使用其他值来估计(插值)。另举一例,考虑一个具有许多相似数据点的数据集,与具有遗漏值的点邻近的点的属性值常常可以用来估计遗漏的值。如果属性是连续的,则可以使用最近邻的平均属性值;如果属性是分类的,则可以取最近邻中最常出现的属性值。为了更具体地解释,考虑地面站记录的降水量,对于未设地面站的区域,降水量可以使用邻近地面站的观测值估计。
在分析时忽略遗漏值 许多数据挖掘方法都可以修改,忽略遗漏值。例如,假定正在对数据对象聚类,需要计算各对数据对象间的相似性。如果某对的一个对象或两个对象都有某些属性有遗漏值,则可以仅使用没有遗漏值的属性来计算相似性。当然,这种相似性只是近似的,但是除非整个属性数据很少,或者遗漏值的数量很大,否则这种误差影响不大。同样地,许多分类方法都可以修改,便于处理遗漏值。
6. 不一致的值
数据可能包含不一致的值。比如地址字段列出了邮政编码和城市名,但是又的邮政编码区域并不包含在对应的城市中。可能是人工输入该信息时录颠倒了两个数字,或许是在手写体扫描时读错了一个数字。无论导致不一致的原因是什么,重要的是能检测出来,并且如果可能的话,纠正这种错误。
有些不一致类型容易检测,例如人的身高不应当是负的。有些情况下,可能需要查阅外部信息源,例如当保险公司处理赔偿要求时,它将对照顾客数据库核对赔偿单上的姓名与地址。
检测到不一致后,有时可以对数据进行更正。产品代码可能有“校验”数字,或者可以通过一个备案的已知产品代码列表,复核产品代码;如果发现它不正确但接近一个已知代码,则纠正它。纠正不一致需要额外的或冗余的信息。
7. 重复数据
数据集可能包含重复或几乎重复的数据对象。许多人都收到过重复的邮件,因为它们稍微以不同的名字多次出现在数据库中。为了检测并删除这种重复,必须处理两个主要问题。首先,如果两个对象实际代表同一个对象,则对应的属性值必然不同,必须解决这些不一致的值;其次,需要避免意外地将两个相似但并非重复的数据对象合并在一起。数据去重复(deduplication)通常用来表示处理这些问题的过程。
在某些情况下,两个或多个对象在数据库的属性度量上是相同的,但是仍然代表不同的对象。这种重复是合法的。但是如果某些算法设计中没有专门考虑这些属性可能相同的对象,就还是可能导致问题。
2.2.2 关于应用的问题
数据质量问题也可以从应用角度考虑,表达为“数据是高质量的,如果它适合预期的应用”。特别是对工商业界,数据质量的这种提议非常有用。
时效性 有些数据收集后就开始老化。比如说,如果数据提供正在发生的现象或过程的快照,如顾客的购买行为或web的浏览模式,则快照只代表有限时间内的真实情况。如果数据已经过时,则基于它的模型和模式也已经过时。
相关性 可用的数据必须包含应用所需要的信息。考虑构造一个模型,预测交通事务发生率。如果忽略了驾驶员的年龄和性别信息,那么除非这些信息可以间接地通过其他属性得到,否则模型的精度可能是有限的。
确保数据集中的对象相关不太容易。一个常见问题是抽样偏倚。指样本包含的不同类型的对象与它们在总体中出现情况不成比例。例如调查数据只反映调查作出相应的那些人的意见。由于数据分析的结果只反映现有的数据,抽样偏倚通常导致不正确的分析。
关于数据的知识 理想情况下,数据集附有描述数据的文档。文档的质量好坏决定它是支持还是干扰气候的分析。例如,如果文档表明若干属性是强相关的,则说明这些属性可能提供了高度冗余的信息,我门可以决定只保留一个。然而,如果文档很糟糕,例如,没有告诉我们特定字段上的遗漏值用-9999指示,则我们的数据分析就可能出问题。其他应该说明的重要特性是数据精度、特征的类型、测量的刻度和数据的来源。
2.3 数据预处理
讨论应当采用哪些预处理步骤,让数据更加适合挖掘。数据预处理是一个广泛的领域,包含大量以复杂得方式相关联的不同策略和技术。我们讨论一些最重要的思想和方法,并试图指出它们之间的相互联系。具体的说,我们将讨论如下主题:
聚集
抽样
维归约
特征子集选择
特征创建
离散化和二元化
变量变换
粗略的说,这些项目分为两类,即选择分析所需要的数据对象和属性以及创建改变属性。这两种情况的目标都是改善数据挖掘分析工作,减少时间,降低成本和提高质量。
术语标记:下面,我们有时将根据习惯用法,使用特征(feature)或变量(variable)指代属性(attribute)。
2.3.1 聚集
有时,“少就是多”,而聚集就是如此。聚集将两个或多个对象合并成单个对象。考虑一个由事务组成的数据集,它记录一年中不同日期在各地商店的商品日销售情况。如下表,对该数据集的事务进行聚集的一种方法,是用一个商店事务替换该商店的所有事务。这把每天出现在一个商店的成百上千个事务记录归约成单个日事务,而数据对象的个数减少为商店的个数。
这里仙儿意见的问题是如何创建聚集事务,即在创建代表单个商店或日期的聚集事务时,如何合并所有记录的每个属性的值。定量属性(如价格)通常通过求和或求平均值进行聚集,定性属性(如商品)可以忽略或汇总在一个商店销售的所有商品的集合。
上表中的数据也可以看做多为数组,其中每个属性是一个维。从这个角度,聚集是杀出属性的过程,或者是压缩特定属性不同值个数的过程,如将日期的可能值从365天压缩到12个月。这种类型的聚集通常用于OLAP。
聚集的动机有多种。首先,数据归约导致的较小数据集需要较少的内存和处理时间,因此可以使用开销更大的数据挖掘算法。其次,通过高层而不是底层数据视图,聚集起到了范围或标度转换的作用。在前面的例子中,在商店位置和月份上的聚集给出数据按月、按商店,而不是按天、按商品的视图。最后,对象或属性群的行为通常比单个对象或属性的行为更加稳定。这反映了统计学事实:相对于被聚集的单个对象,诸如平均值、总数等聚集量具有较小的变异性。对于总数,实际变差大于单个对象的变差,但是变差的百分比较小;而对于均值,实际变差小于单个对象的变差。聚集的缺点是可能丢失有趣的细节。在商店的例子中,按月的聚集就丢失了星期几具有最高销售额的信息。
2.3.2 抽样
抽样是一种选择数据对象子集进行分析的常用方法。在统计学中,抽样长期用于数据的事先调查和最终的数据分析。在数据挖掘中,抽样也非常有用。然而,在统计学和数据挖掘中,抽样的动机并不相同。统计学使用抽样是因为感兴趣的整个数据集的费用太高、太费时间,而数据挖掘使用抽样是因为处理所有的数据的费用太高、太费时间。在某些情况下,使用抽样的算法可以压缩数据量,以便可以使用更好但开销较大的数据挖掘算法。
有效抽样的主要原理如下:如果样本是有代表性的,则使用样本与使用数据集的效果几乎一样,而样本是由代表性的。前提是它近似地具有与元数据集相同的性质。如果数据对象的均值是感兴趣的性质,而样本具有近似于原始数据集的均值,则样本就是有代表性的。由于抽样是一个统计过程,特定样本的代表性是变化的。因此我们所能做的最好的抽样方案就是选择一个确保以很高的概率得到有代表性的样本。如下所述,这设计选择适当的样本容量和抽样技术。
1. 抽样方法
有许多抽样技术,但是这里只介绍少数最基本的抽样技术和它们的变形。最简单的抽样是简单随机抽样(simple random sampling)。对于这种抽样,选取任何特定项的概率相等。随机抽样有两种变形:(1)无放回抽样---每个选中项立即从构成总体的所有对象集中删除;(2)有放回抽样---对象被选中时不从总体中删除。在有放回抽样中,相同的对象可能被多次抽出。当样本与数据集相比相对较小时,两种方法产生的样本差别不大。但是,对于,对于分析,有放回抽样较为简单,因为在抽样过程中,每个对象被选中的概率保持不变。
当总体由不同类型的对象组成,每种类型的对象数量差别很大时,简单随机抽样不能充分地代表不太频繁出现的对象类型。当分析需要所有类型的代表时,这可能出现问题。例如,当为稀有类构造分类模型时,样本中适当地提供稀有类是至关重要的,因此需要提供具有不同频率的感兴趣的项的抽样方案。分层抽样(stratified sampling)就是这样的方法,它从预先指定的组开始抽样。在最简单的情况下,尽管每组的大小不同,但是从每组抽取的对象个数相同。另一种变形是从每一组抽取的对象数量正比于改组的大小。
例2.8 抽样与信息损失 一旦选定抽样技术,就需要选择样本容量。较大的样本容量增大了样本具有代表性的概率,但也抵消了抽样带来的许多好处。反过来,使用较小容量的样本,可能丢失模式,或检测除错误的模式。如下图(a)显示包含8000个二维点的数据集,而图(b)和图(c)显示从该数据集抽取的容量分别为2000和500的样本。该数据集的大部分结构都出现在2000个点的样本中,但是许多结构在500个点的样本中丢失了。
例2.9 确定适当的样本容量 为了说明确定合适的样本容量需要系统的方法,考虑下面的任务。给定一个数据集,它包含少量容量大致相等的组,从每组至少找出一个代表点。假定每个组内的对象高度相似,但是不同组中的对象不太相似,还假定组的个数不多(例如10个组)。图(a)显示了一个理想簇的集合。这些点可能从中抽取。
使用抽样可以有效地解决该问题。一种方法是取数据点的一个小样本,逐对计算点之间的相似性,然后形成高度相似的点。从这些组每组取一个点,则可以得到具有代表性的点的集合。然而,按照该方法,我们需要确定样本的容量,它以很高的概率确保得到的期望的结果,即从每个簇至少找出一个代表点。图(b)显示随着样本容量从10变化到60时,从10个组的每一个得到一个对象的概率。有趣的是,使用容量为20的样本,只有很小的机会得到包含所有10个簇的样本,即便使用30的样本,得到不包含所有10个簇中对象的样本的几率也很高。该问题将在第8张讨论聚类中进一步考察。
2. 渐进抽样
合适的样本容量可能很难确定,因此有时需要使用自适应(adaptive)或渐进抽样(progressive sampling)方法。这些方法从一个小样本开始,然后增加样本容量直至得到足够容量的样本。尽管这种技术不需要在开始就确定正确的样本容量,但是需要评估样本的方法,确定它是否足够大。
例如,假定使用渐进抽样来学习一个预测模型。尽管预测模式的准确率随样本容量增加,但是在某一点准确率的增加趋于稳定。我们希望在稳定点停止增加样本容量。通过掌握模型准确率随样本主键增大的变化情况,并通过选取接近于当前容量的其他样本,我们可以估计出与稳定点的接近程度,从而停止抽样。
2.3.3 维归约
数据集可能包含大量特征。考虑一个文档的集合,其中每个文档是一个向量,其分量是文档中出现的每个词的频率。在这种情况下,通常有成千上万的属性(分量),每个代表词汇表中的一个词。再看一个例子,考虑包含过去30年各种股票日收盘价的时间序列数据集。在这种情况下,属性也是特定天的价格,也数以千计。
维归约有多方面的好处。关键好处是,如果维度较低,许多数据挖掘算法的效果就会更好。这一部分是因为维归约可以删除不想管的特征并降低噪声,一部分是因为维灾难。(维灾难在下面解释)。另一个好处是维归约可以使模型更容易理解,因为模型可能只涉及较少的属性。此外,维归约也可以更容易让数据可视化。即使维归约没有将数据归约到二维或者三维,数据也可以通过观察属性对或三元组属性达到可视化,并且这种组合的数目也会大大减少。最后,使用维归约降低了数据挖掘算法的时间和内存需求。
术语“维归约”通常用于这样的技术:通过创建新属性,将一些旧属性合并在一起来降低数据集的维度。通过选择旧属性的子集得到新属性,这种维归约称为特征子集选择或特征选择。特征选择将在2.3.4节讨论。
下面介绍两个重要的主题:维灾难和基于现行代数方法(如主成分分析)的维归约技术。
1. 维灾难
维灾难是指这样的现象:随着数据维度的增加,许多数据分析变得非常困难。特别是随着维度增加,数据在它所占据的空间中越来越稀疏。对于分类,这可能意味没有足够的数据对象来创建模型,将所有可能的对象可靠地指派到一个类。对于聚类,点之间的module和距离的定义失去了意义。结果是,对于高维数据,许多分类和聚类算法都麻烦缠身---分类准确率降低,聚类质量下降。
2. 维归约的现行代数技术
维归约的一些最常用的方法是使用现行代数技术,将数据由高维空间投影到低维空间,特别是对于连续数据。主成分分析(Principal Components Analysis,PCA)是一种用于连续属性的现行代数技术,它找出新的属性(主成分),这些属性是原属性的线性组合,是相互正交的,并且捕获了数据的最大变差。例如,前两个主成分是两个正交属性,是原属性的现行组合,尽可能多地捕获了数据的变差。奇异值分解(Singular Value Decomposition,SVD)是一种现行代数技术,它与PCA有关,并且也用于维归约。
2.3.4 特征子集选择
降低维度的另一种方法是仅使用特征的一个子集。尽管看来这种方法可能丢失信息,但是在存在冗余或不相关的特征的时候,情况并非如此。冗余特征重复了包含在一个或多个其他属性中的许多或所有信息。例如,一种产品的购买价格和所支付的销售税额包含许多相同的信息。不想管特征包含对于手头的数据挖掘任务几乎完全没用的信息,例如学生的ID号码对于预测学生的总平均成绩是不相关的。冗余和不相关的特征可能降低分类的准确率,影响所发现的聚类的质量。
尽管使用常识或领域知识可以立即消除一些不相关的和冗余的属性,但是选择最佳的特征子集通常需要系统的方法。特征选择的理想方法是:将所有可能的特征子集作为感兴趣的数据挖掘算法的输入,然后选取产生最好结果的子集。这种方法的优点是反映了最终使用的数据挖掘算法的目的和偏爱。然而,由于涉及n个属性的子集多大2的n次方个,这种方法在大部分情况下行不通,因此需要其他策略。有三种标准的特征选择方法:嵌入、过滤和包装。
嵌入方法(embedded approach) 特征选择作为数据挖掘算法的一部分是理所当然的。特别是在数据挖掘算法运行期间,算法本身决定使用哪些属性和忽略哪些属性。构造决策树分类器的算法通常以这种方式运行。
过滤方法(filter approach) 使用某种独立于数据挖掘任务的方法。在数据挖掘算法运行前进行特征选择。例如我们可以选择属性的集合,它的属性对之间的相关度尽可能低。
包装方法(wrapper approach) 这些方法将目标数据挖掘算法作为黑盒,使用类似于前面介绍的理想算法,但通常并不枚举所有可能的子集来找出最佳属性子集。
由于嵌入方法与具体的算法有关,这里只进一步讨论过滤和包装方法。
1. 特征子集选择体系结构
可以讲过滤和包装方法放到一个共同的体系结构中。特征选择过程可以看做由四部分组成:子集评估度量、控制新的特征子集产生的搜索策略、停止搜索判断和验证过程。过滤方法和包装方法的唯一不同是它们使用了不同的特征子集评估方法。对于包装方法,子集评估使用目标数据挖掘算法;对于过滤方法,子集评估技术不同于目标数据挖掘算法。下面的讨论提供了该方法的一些细节。如下图
从概念上讲,特征子集选择是搜索所有可能的特征子集的过程。可以使用许多不同类型的搜索策略,但是搜索策略的计算花费应当较低,并且应当找到最优或近似最优的特征子集。通常不可能同时满足这两个要求,因此需要折中权衡。
搜索的一个不可缺少的组成部分是评估步骤,根据已经考虑的子集评价当前的特征子集。这需要一种评估度量,针对诸如分类或聚类等数据挖掘任务,确定属性特征子集的质量。对于过滤方法,这种度量试图预测实际的数据挖掘算法在给定的属性集上执行的效果如何;对于包装方法,评估包括实际运行且目标数据挖掘应用,子集评估函数就是通常用于度量数据挖掘结果的评判标准。
因为子集的数量可能很大,考察所有的子集可能不现实,因此需要某种停止搜索判断。其策略通常基于如下一个或多个条件:迭代次数,子集评估的度量值是否最优或超过给定的阈值,一个特定大小的子集是否已经得到,大小和评估标准是否同时达到,使用搜索策略得到的选择是否可以实现改进。
最后,一旦选定特征子集,就要验证目标数据挖掘算法在选定子集上的结果。一种直截了当的评估方法时用全部特征的集合运行算法,并将全部结果与使用该特征子集得到的结果进行比较。如果顺利的话,特征子集产生的结果将比使用所有特征产生的结果更好,或者至少几乎一样好。另一个验证方法是使用一些不同的特征选择算法得到特征子集,然后比较数据挖掘算法在每个子集上的运行结果。
2. 特征加权
特征加权是另一种保留或删除特征的办法。特征越重要,所赋予的权值越大,而不太重要的特征赋予较小的权值。有时,这些权值可以根据特征的相对重要性的领域知识确定,也可以自动确定。例如,有些分类方法,如支持向量机,产生分类模型,其中每个特征都赋予一个权值。具有较大权值的特征在模型中所起的作用更加重要。在计算预算相似度时进行的对象规范化也可以看做一类特征加权。
2.3.5 特征创建
常常可以由原来的属性创建新的属性集,更有效地捕获数据集中的重要信息。此外,新属性的数目可能比原属性少,使得我们可以获得前面介绍的维归约带来的所有好处。下面介绍三种创建新属性的相关方法:特征提取、映射数据到新的空间和特征构造。
1、特征提取
由原始数据创建新的特征集称作特征提取(featur extraction)。考虑照片的集合,按照照片是否包含人脸分类。原始数据是像素的集合,因此对于许多分类算法都不合适。然而,如果对数据进行处理,提供一些较高层次的特征,诸如与人脸相关的某些类型的边和区域等,则会有更多的分类技术可以用于该问题。
可是吗,最常使用的特征提取技术都是高度针对具体领域的。对于特定的领域,如图像处理,在过去一段时间已经开发了各种特征和提取特征的技术,但是这些技术在其他领域的应用却是有限的。因为,一旦数据挖掘用于一个相对较新的领域,一个关键任务就是开发新的特征和特征提取方法。
2. 映射数据到新的空间
使用一种完全不同的视角挖掘数据可能揭示出重要和有趣的特征。例如,考虑时间序列数据,它们常常包含周期模式。如果只有单个周期模式,并且噪声不多,则容易检测到该模式;另一方面,如果有大量周期模式,并且存在大量噪声,则很难检测这些模式。尽管如此,通过对该时间序列实施傅里叶变换(Fourier transform),将它转换成频率信息明显的表示,就能检测到这些模式。在下面的例子中,不必知道傅里叶变换的细节,只需要知道对于时间序列,傅里叶变换产生其属性与频率有关的新数据对象就足够。
例2.10 傅里叶分析 图(b)中的时间序列是其他是哪个时间序列的和,其中两个显示在图(a)中,其频率分别是每秒7个和17个周期,第三个时间序列是随机早上。图(c)显示功率频谱。在对原时间序列施加傅里叶变换后,可以计算功率频谱。尽管有噪声,图中有两个尖峰,对应于两个原来的、无噪声的时间序列的周期。再说一遍,本例的要点是:更好的特征可以揭示数据的重要性质。
也可以采用许多其他类型的变换。除傅里叶变换外,对于时间序列和其他类型的数据,径证实小波变换(waveler transform)也是非常有用的。
3. 特征构造
有时,原始数据集的特征具有必要的信息,但其形式不适合数据挖掘算法。在这种情况下,一个或多个由原特征构造的新特征可能比原特征更有用。
例2.11 密度 为了解释这一点,考虑一个包含人工制品信息的历史数据集。该数据集包含每个人工制品的体积和质量,以及其他信息。为简单起见,假定这些人工制品使用少量材料制造,并且我们希望根据制造材料对它们分类。在此情况下,由质量和体积构造的密度特征可以很直接地产生准确的分类。尽管有一些人试图通过考察已有特征的简单数学组合来自动地进行特征构造,但是最常见的方法还是使用专家的意见构造特征。
2.3.6 离散化和二元化
有些数据挖掘算法,特别是某些分类算法,要求数据是分类属性形式。发现关联模式的算法要求数据是二元属性形式。这样,常常需要将连续属性变换成分类属性(离散化,discretization),并且连续和离散属性可能都需要变换成一个或多个二元属性(二元化,binarization)。此外,如果一个分类属性具有大量不通知(类别),或者某些值出现不频繁,则对于某些数据挖掘任务,通过合并某些值减少类别的数目可能是有益的。
与特征选择一样,最佳的离散化和二元方法是“对于用来分析数据的数据挖掘算法,产生最好结果”的方法。直接使用这种判别标准通常是不实际的。因此,离散化和二元化一般要满足这样一种判别标准,它与所考虑的数据挖掘任务的性能好坏直接相关。
1. 二元化
一种分类属性二元化的简单技术如下:如果有m个分类值,则将每个原始值唯一地赋予区间[0,m-1]中的一个整数。如果属性是有序的,则赋值必须保持序关系。(注意,即使属性原来就用整数表示,但如果这些整数不在区间[0,m-1]中,则该过程也是必须的。)然后,将这m个整数的每一个都变换成一个二进制数。由于需要n=[log2m]个二进制表示这些整数,因此要使用n个二元属性表示这些二进制数。例如,一个具有5个值[awful,poor,OK,good,great]的分类变量需要三个二元变量x1、x2、x3。转换表如下所示:
这样的变换可能导致复杂化,如无意之中建立了转换后的属性之间的联系。例如在表2-5中,属性x2和x3是相关的,因为good值使用这两个属性表示。此外,关联分析需要非对称的二元属性,其中只有属性的出现才是重要的。因此,对于关联问题,需要为每一个分类值引入一个二元属性,如表2-6所示。如果结果属性的个数太多,则可以再二元化之前使用下面介绍的技术减少分类纸的个数。
同样,对于关联问题,可能需要用两个非对称的二元属性替换单个二元属性。考虑记录人的性别的二元属性,对于传统关联规则算法,该信息需要转换成两个非对称的二元属性,其中一个仅当是男性时为1,而另一个仅当是女性时为1。
2. 连续属性离散化
通常,离散化应用于在分类或关联分析中使用到的属性上。一般来说,离散化的效果取决于所使用的算法,以及用到的其他属性。然而,属性离散化通常单独考虑。
连续属性变换成分类属性涉及两个子任务:决定需要多少个分类值,以及确定如何将连续属性值映射到这些分类值。在第一步中,将连续属性值排序后,通过制定n-1个分割点把他们分成n个区间。在颇为平凡的第二步中,将一个区间中的所有值映射到相同的分类值。因此,离散化问题就是决定选择多少个分割点和确定分割点位置的问题。结果可以用区间集合{(x0,x1],(x1,x2],...,(xn-1,xn]}表示,其中x0和xn可以分别为±∞。
非监督离散化 用于分类的离散化方法之间的根本区别在于使用类信息(监督,supervised)还是不使用类信息(非监督,unsupervised)。如果不使用类信息,则常使用一些相对简单的方法。例如,等宽方法将属性的值域划分成具有相同宽度的区间,而区间的个数由用户指定。这种方法可能受离群点的影响而性能不佳,因此等频率或等深方法通常更为可取。等频率方法试图将相同数量的对象放进每个区间。作为非监督离散化的另一个例子,可以使用诸如K均值等聚类方法。最后,目测检查数据有时也可能是一种有效地方法。
例2.12 离散化技术 本例解释如何对实际数据集使用这些技术。如图(a)显示了属于四个不同组的数据点,以及两个离群点---位于两边的大点。可以使用上述技术将这些数据点的x值离散化成四个分类值。尽管目测检查该数据的方法效果很好,但不是自动的,因此我们主要讨论其他三种方法。使用等宽、等频率和K均值技术产生的分割点分别如下图,图中分割点用虚线表示。如果我们用不同组的不同对象被指派到相同分类值的程度来度量离散化技术的性能,则K均值性能最好,其次是等频率,最后是等宽。
监督离散化 上面介绍的离散化方法通常比不离散化好。但是记住最终的目的并使用附加的信息(类标号)常常能够产生更好的结果。这并不奇怪,因为未使用类标号知识锁构造的区间常常包含混合的类标号。一种概念上的简单方法是以极大化区间纯度的方法确定分割点。然而,时间中这种方法可能需要人为确定区间的纯度和最小的区间大小。为了解决这一问题,一些基于统计学的方法用每个属性值来分割区间,并通过合并类似于根据统计检验得出的相邻区间来创建较大的区间基于熵的方法是最有前途的离散化方法之一,我们将给出一种简单的基于熵的方法。
首先,需要定义熵(entropy)。设k是不同的类标号数,mi是某划分的第i个区间中值得个数,而mij是区间i中类j的值的个数。第i个区间的熵ei由如下公式给出:
其中,pij=mij/mi是第i个区间中类j的概率。该划分的总熵e是每个区间的熵的甲醛平均,即:
其中,m是值的个数,wt=mi/m是第i个区间的值得比例,而n是区间个数。直观上,区间的熵是区间纯度的度量,如果一个区间只包含一个类的值,则其熵为0并且不影响总熵。如果一个区间中的值类出现的频率相等,则其熵最大。
一种划分连续属性的简单方法是:开始,将初始值切分成两部分,让两个结果区间产生最小熵。该技术只需要把每个值看做可能的分割点即可,因为假定区间包含有序值得集合。然后,取一个区间,通常选取具有最大熵的区间,重复此分割过程,直到区间的个数达到用户指定的个数,或者满足终止条件。
例2.13 两个属性离散化 该方法用来独立地离散化二维数据的属性x和y。在图(a)的第一个离散化中,属性x和y被划分成三个区间。在图(b)所示的第二个离散化汇总,属性x和y被划分成5个区间。
这个简单的例子解释了离散化的两个特点。首先,在二维中,点类是很好分开的,但在一维中,情况并非如此。一般而言,分别离散化每个属性通常只保证次最优的结果。其次,五个区间比三个好,但是至少从熵的角度看,六个区间对离散化的改善不大。
3. 具有过多值得分类属性
分类属性有时可能具有过多的值。如果分类属性是序数属性,则可以使用类似于处理连续属性的技术,以减少分类值得个数。然而,如果分类属性是标称的,就需要其他方法。考虑一所大学,它有许多系,因而系名属性可能具有十个不同的值。在这种情况下,我们可以使用系之间联系的知识,将系合并成较大的组,如工程学、社会科学或生物科学。如果领域知识不能提供有用的指导,或者这样的方法会导致很差的分类性能,则需要使用更为经验性的方法,如仅当分组结果能提高分类准确率或达到某种其他数据挖掘目标时,才将值聚集到一起。
2.3.7 变量变换
变量变换(variable transformation)是指用于变量的所有值得变换。换言之,对于每个对象,变换都作用域该对象的变量值。例如,如果只考虑变量的两级,则可以通过取绝对值对变量进行变换。接下来的部分,我们讨论两种重要的变量变换类型:简单函数变换和规范化。
1. 简单函数
对于这种类型的变量变换,一个简单函数分别作用域每一个值。如果x是变量,这种变换的例子包括![]() 。在统计学中,变量变换(特别是平方根、对数和倒数变换)长用来将不具有高斯(正态)分布的数据变换成具有高斯(正态)分布的数据。尽管这可能很重要,但是在数据挖掘中,其他理由可能更重要。假定感兴趣的变量是一次绘画中的数据字节数,并且字节数的值域范围为1到10亿。这是一个很大的值域,使用常用对数变黄将其进行压缩可能是有益的。这样的话,传输10^8和10^9字节的会话比传说10字节和1000字节的绘画更为相似(9-8=1掉3-1=2)。对于某些应用,如网络入侵检测,可能需要如此,因为前两个会话多半表示传输两个大文件,而后两个会话可能是两个完全不同的类型。
。在统计学中,变量变换(特别是平方根、对数和倒数变换)长用来将不具有高斯(正态)分布的数据变换成具有高斯(正态)分布的数据。尽管这可能很重要,但是在数据挖掘中,其他理由可能更重要。假定感兴趣的变量是一次绘画中的数据字节数,并且字节数的值域范围为1到10亿。这是一个很大的值域,使用常用对数变黄将其进行压缩可能是有益的。这样的话,传输10^8和10^9字节的会话比传说10字节和1000字节的绘画更为相似(9-8=1掉3-1=2)。对于某些应用,如网络入侵检测,可能需要如此,因为前两个会话多半表示传输两个大文件,而后两个会话可能是两个完全不同的类型。
使用变量变换时需要小心,因为它们改变了数据的特性。尽管有时需要这样做,但是如果变换的特性没有深入理解,则可能出现问题。例如,变换1/x虽然压缩了大于1的值,但是却放大了0和1之间的值。为了帮助弄清楚一个变换的效果,重要的是要问如下问题:需要保序吗?变换作用于所有的值,特别是负值和0值吗?变换对0和1之间的值有何特别影响?
2. 规范化或标准化
另一种常见的变量变换类型是变量的标准化(standardization)或规范化(normalization)。在数据挖掘中,这两个属于常常互换。然而,在统计学中,术语规范化可能与使变量正态(高斯)的变换相混淆。标准化或规范化的目标是使整个值的集合具有特定的性质。一个传统的例子是统计学中的“对变量标准化”。如果x是属性值的均值,而Sx是它们的标准差,则变换![]() 创建一个新的变量,它具有均值0和标准差1。如果要以某种方法组合不同的变量,则为了避免具有较大值域的变量左右计算结果,这种变换常常是必须的。例如,考虑使用年龄和收入两个变量对人进行比较。对于任意两个人,收入之差的绝对值多半比年龄之差的绝对值大很多。如果没有考虑到年龄和收入值域的差别,则对人的比较将被收入之差所左右。例如,如果两个人之间的相似性或相异性使用本章后面的相似度或相异性度量来计算,则在很多情况下(如欧几里得距离)收入值将左右计算结果。
创建一个新的变量,它具有均值0和标准差1。如果要以某种方法组合不同的变量,则为了避免具有较大值域的变量左右计算结果,这种变换常常是必须的。例如,考虑使用年龄和收入两个变量对人进行比较。对于任意两个人,收入之差的绝对值多半比年龄之差的绝对值大很多。如果没有考虑到年龄和收入值域的差别,则对人的比较将被收入之差所左右。例如,如果两个人之间的相似性或相异性使用本章后面的相似度或相异性度量来计算,则在很多情况下(如欧几里得距离)收入值将左右计算结果。
均值和标准差受离群点的影响很大,因此通常需要修改上述变换。首先,用中位数(median)取代均值,其次,用绝对标准差(absolute standard deviation)取代标准差。例如,如果x是变量,则x的绝对标准差为![]() ,其中xi是变量x的第i个值,m是对象的个数,而μ是均值或中位数。存在离群点时,计算值集的位置(中心)和发散估计的其他方法分别在3.2.3和3.2.4节介绍。这些度量可以用来定义标准化变换。
,其中xi是变量x的第i个值,m是对象的个数,而μ是均值或中位数。存在离群点时,计算值集的位置(中心)和发散估计的其他方法分别在3.2.3和3.2.4节介绍。这些度量可以用来定义标准化变换。
2.4 相似性和相异性的度量
相似性和相异性是重要的概念。因为它们被许多数据挖掘技术所使用。如聚类、最近邻分类和异常检测等。在许多情况下,一旦计算出相似性或相异性,就不再需要原始数据了。这种方法可以看做将数据变换到相似性(相异性)空间,然后进行分析。
首先,讨论基本要素---相似性和相异性的高层定义,并讨论它们之间的联系。为方便起见,使用术语邻近度表示相似性或相异性。由于两个对象之间的邻近度是两个对象对应属性之间的邻近度的函数,因此我们首先介绍如何度量仅包含一个简单属性的对象之间的邻近度,然后考虑具有多个属性的对象的邻近度度量。这包括相关和欧几里得距离度量,以及Jaccard和余弦相似度量。前二者适用于时间序列这样的稠密数据或二维点。后二者适用于像文档这样的稀疏数据。接下来,考虑与邻近度度量相关的若干重要问题。本节最后简略讨论如何选择正确的邻近度度量。
2.4.1 基础
1. 定义
两个对象之间的相似度(similarity)的非正式定义是这两个对象相似程度的数值度量。因而,两个对象越相似,它们的相似度就越高。通常相似度是非负的,并常常在0(不相似)和1(完全相似)之间取值。
两个对象之间的相异度(dissimilarity)是这两个对象差异程度的数值度量。对象越类似,它们的相异度就越低。通常,术语距离(distance)用作相异度的同义词,正如我们介绍的,距离常常用来表示特定类型的相异度。有时,相异度在区间[0,1]中取值,但是相异度在0和∞之间取值也很常见。
2. 变换
通常使用变换把相似度转换成相异度或相反,或者把邻近度变换到一个特定区间,如[0,1]。例如,我们可能有相似度,其值域从1到10,但是我们打算使用的特定算法或软件只能处理相异度,或只能处理[0,1]区间的相似度。之所以在这里讨论这些问题,是因为在稍后讨论邻近度时,我们将使用这种变换。此外,这些问题相对独立于特定的邻近度度量。
通常,邻近度度量(特别是相似度)被定义为或变换到区间[0,1]中的值。这样做的动机是使用一种适当的尺度,由邻近度的值表明两个对象之间的相似程度。这种变换通常是比较直接了当的。例如,如果对象之间的相似度在1和10之间变换,则我们可以使用如下变换将它变换到[0,1]区间:s'=(s-1)/9,其中s和s'分别是相似度的原值和心智。一般来说,相似度到[0,1]区间的变换由如下表达式给出:s'=(s-min_S)/(max_S-min_S),其中max_S和min_S分别是相似度的最大值和最小值。类似地,具有有限值域的相异度也能用d'=(d-min_D)/(max_D-min_D)映射到[0,1]区间。
然而,将邻近度映射到[0,1]区间可能非常复杂。例如,如果邻近度度量原来在区间[0,∞]上取值,则需要使用非线性变换,并且在新的尺度上,值之间不再具有相同的联系。对于从0变化到∞的相异度度量,考虑变换d'=d/(1+d),相异度0、0.5、2、10、100和1000分别被变换到0、0.33、0.67、0.90、0.99和0.999。在原来相异性尺度上较大的值被压缩到1附近,但是否希望如此取决于应用。另一个问题是邻近度度量的含义可能会被改变。例如,相关性是一种相似性度量,在区间[-1,1]上取值,通过取绝对值将这些映射到[0,1]区间丢失了符号信息,而对于某些应用,符号信息可能是重要的。
将相似度变换成相异度或相反也是比较直截了当的,尽管我们可能再次面临保持度量的含义问题和将现行尺度改变成非线性尺度的问题。如果相似度落在[0,1]区间,则相异度可以定义为d=1-s。另一种简单方法是定义相似度为负的相异度。例如相异度0,1,10和100可以变换成相似度0,-1,-10和-100。
一般来说,任何单调函数都可以用来将相异度转换到相似度。当然,在将相似度变换到相异度,或者在将邻近度的值变换到新的尺度时,也必须考虑一些其他因素,我们提到过一些问题,设计保持意义、扰乱标度和数据分析工具的需要,但是肯定还有其他问题。
2.4.2 简单属性之间的相似度和相异度
具有若干属性的对象之间的邻近度用单个属性的邻近度的组合来定义,因此我们首先讨论具有单个属性的对象之间的邻近度。考虑由一个标称属性描述的对象,对于两个这样的对象,相似意味什么呢?由于标称属性只携带了对象的相异性信息,因此我们只能说两个对象有相同的值或者没有。因而在这种情况下,如果属性值匹配,则相似度定义为1,否则为0;相异度用相反的方法定义:如果属性值匹配,相异度为0,否则为1。
对具有单个序数属性的对象,情况更为复杂。因为必须考虑序信息。考虑一个在标度{poor,fair,OK,good,wonderful}上2测量产品质量的属性。一个评定为wonderful的产品P1与一个评定为good的产品P2应当比它与一个评定为OK的产品P3更接近,为了量化这种观察,序数属性的值常常映射到从0或1开始的相继整数,例如{poor=0,fair=1,OK=2,good=3,wonderful=4}。于是,P1和P2之间的之间的相似度d(P1,P2)=3-2=1,或者,如果我们希望相异度在0和1之间取值,d(P1,P2)=(3-2)/4=0.25;序数属性的相似度可以定义为s=1-d。
序数属性相似度的这种定义可能使人感到有点担心。因为这里我们定义了相等的区间,而事实并非如此。如果根据实际情况,我们应该计算出区间或比率属性。值fair和good的差真和ok与wonderful的差相同吗?可能不相同,但是在实践中,我们的选择是有限的,并且在缺乏更多信息的情况下,这是定义序数属性之间邻近度的标准方法。
对于区间或比率属性,两个对象之间的相异性的自然度量是它们的值之差的绝对值。例如,可能将现在的体重与一年前的体重相比较,说“中了10磅”。在这类情况下,相异度通常在0和∞之间,而不是0和1之间取值。
如下表总结了这些讨论。在该标中,x和y是两个对象,它们具有一个指明类型的属性,d(x,y)和s(x,y)分别是x和y之间的相异度和相似度(分别用d和s表示)。其他方法也是可能的,但是表中的这些是最常用的。
下面谅解介绍更复杂的涉及多个属性的对象之间的邻近性度量:(1)数据对象之间的相异度;(2)数据对象之间的相似度。这样分节可以更自然地展示使用各种邻近度度量的基本动机,然而,我们要强调的是使用上述技术,相似度可以变换成相异度,反之亦然。
2.4.3 数据对象之间的相异度
讨论各种不同类型的相异度。从讨论距离(距离是具有特定性质的相异度)开始,然后给出一些更一般的相异度类型的例子。
距离
首先给出一些例子,然后使用距离的常见性质正式地介绍距离。一维、二维、三维或高维空间中有两个点x和y之间的欧几里得距离(Euclidean distance)d由如下熟悉的公式定义:
其中,n是维数,而xk和yk分别是x和y的第k个属性值(分量)。用下图解释该公式,它们展示了这个点集、这些点的x和y坐标以及包含这些点之间距离的距离矩阵(distance matrix)。
上述公式给出的欧几里得距离可以闵可夫斯基距离(Minkowski distance)来推广:
其中r是参数。下面是闵可夫斯基距离的三个最常见的例子。
r=1,城市街区(也称曼哈顿、出租车、L1范数)距离。一个常见的例子是汉明距离(Hamming distance),他是两个具有二元属性的对象(即两个二元向量)之间不同的二进制位个数。
r=2,欧几里得距离(L2范数)。
r=∞,上确界(Lmax或L∞范数)距离。这是对象属性之间的最大距离。
注意不要讲参数r与维数(属性数)n混淆。欧几里得距离、曼哈顿距离和上确界距离是对n的所有制定义的,并且指定了将每个维(属性)上的差组合成总距离的不同方法。
如下表给出数据的L1距离和L∞距离的邻近度矩阵。注意,所有的距离矩阵都是堆成的。
距离具有一些众所周知的性质。如果d(x,y)是两个点x和y之间的距离,则如下性质成立:
(1)非负性
(2)对称性
(3)三角不等式
满足以上三个性质的测度称为度量。这里介绍的三个性质是有用的,数学上也是令人满意的。此外,如果三角不等式成立,则该性质可以用来提高依赖于距离的技术的效率。
2.4.4 数据对象之间的相似度
对于相似度,三角不等式通常不成立,但是对称性和非负性质通常成立。更明确的说,如果s(x,y)是数据点x和y之间的相似度,则相似度具有如下典型性质:
(1)仅当x=y时,s(x,y)=1.
(2)对于所有x和y,s(x,y)=s(y,x)。
可以讲相似度简单地变换成一种度量距离。稍后讨论的余弦相似度和Jaccard相似性度量就是两个例子。此外,对于特定的相似性度量,还可能在两个对象相似性上导出本质上与三角不等式类似的数学约束。
2.4.5 邻近性度量的例子
本节给出一些相似性和相异性度量的具体例子。
1. 二元数据的相似性度量
两个仅包含二元属性的对象之间的相似性度量也称为相似系数(similarity coefficient),并且通常在0和1之间取值。值为1表明两个对象完全相似,而值为0表明对象一点也不相似。有许多理由表明在特定情形下,一种系数为何比另一种好。
设x和y是两个对象,都由n个二元属性组成。这样的两个对象(即low二元向量)的比较可生成如下四个量:
f00=x取0并且y取0的属性个数
f01=x取0并且y取1的属性个数
f10=x取1并且y取0的属性个数
f11=x取1并且y取1的属性个数
简单匹配系数(SMC) 一种常用的相似性系数是简单匹配稀疏,定义如下:
该度量对出现和不出现都进行计数。因此SMC可以再一个包含是非题的测验中用来发现回答问题相似的学生。
Jaccard系数(Jaccard Coefficient) 假定x和y是两个数据对象,代表一个事务矩阵的两行。如果每个非对称的二元属性对应于商店的一种商品,则1表示该商品被购买,而0表示商品未被购买。由于未被顾客购买的商品数远大于被其购买的商品数,因而像SMC这样的相似性度量将会判定所有的事务都是类似的。这样,常常使用Jaccard稀疏来处理仅包含非对称的二元属性的对象。Jaccard系数通常用符号J表示,由如下等式定义:
例2.17 SMC和Jaccard相似性系数 为了解释这两种相似性度量之间的差别,我们对如下二元向量计算SMC和J:
x=(1,0,0,0,0,0,0,0,0,0)
y=(0,0,0,0,0,0,1,0,0,1)
f01=2 x取0并且y取1的属性个数
f10=1 x取1并且y取0的属性个数
f00=7 x取0并且y取0的属性个数
f11=0 x取1并且y取1的属性个数
2. 余弦相似度
文档用向量表示,向量的每个属性代表一个特定的词在文档中出现的频率。当然,实际情况要复杂得多,因为需要忽略常用词,并使用各种技术处理同一个词的不同形式、不同的文档长度以及不同的词频。
尽管文档具有数以万计的属性(词),但是每个文档向量都是稀疏的,因为它具有相对较少的非零属性值。(文档规范化并不对零词目创建非零词目,即文档规范化保持稀疏性)。这样与实务数据一样,相似性不能依赖共享0的个数,因为任意两个文档多半都不会包含许多相同的词,从而如果统计0-0匹配,则大多数文档都与其他大部分文档非常类似。因此,文档的相似性度量不仅应当像Jaccard度量一样需要忽略0-0匹配,而且还必须能够处理非二元向量。下面定义的余弦相似度(cosine similarity)就是文档相似性最常用的度量之一。如果x和y是两个文档向量,则
例2.18 两个文档向量的余弦相似度 该例计算下面两个数据对象的余弦相似度,这些数据对象可能代表文档向量:
如下图所示,余弦相似度实际上是x和y之间夹角的度量。这样,如果余弦相似度为1,则x和y之间夹角为0°,并且除大小之外,x和y是相同的;如果余弦相似度为0,则x和y之间夹角为90°没并且它们不包含任何相同的词。
也可以写成如下的形式:
x和y被它们的长度除,将它们规范化成具有长度1.这意味着在计算相似度时,预先相似度不考虑两个数据对象的量值。(当量值是重要的时,欧几里得距离可能是一种更好的选择)。对于长度为1的向量,余弦度量可以通过简单地取点积计算。从而,在需要计算大量对象之间的余弦相似度时,将对象规范化,使之具有单位长度可以减少计算时间。
3. 广义Jaccard系数
广义Jaccard系数可以用于文档数据,并在二元属性情况下归约为Jaccard系数。广义Jaccard系数又称为Tanimoto系数。该系数用EJ表示,在下式定义:
4. 相关性
两个具有二元变量或连续变量的数据对象之间的相关性是对象属性之间线性联系的度量。更准确地,两个数据对象x和y之间的皮尔森相关系数由下式定义:
例2.19 完全相关 相关度总是在-1到1之间取值。相关度为1(-1)意味x和y具有完全正(负)线性关系,即![]() ,其中a和b是常数。下面两个x和y的值集分别给出相关度为-1和+1的情况。为简单起见,第一组中取x和y的均值为0。
,其中a和b是常数。下面两个x和y的值集分别给出相关度为-1和+1的情况。为简单起见,第一组中取x和y的均值为0。
例2.20 非线性关系 如果相关度为0,则两个数据对象的属性之间不存在线性关系。然而,仍然可能存在非线性关系。在下面的例子中,数据对象的属性之间存在非线性关系![]() ,但是它们的相关度为0。
,但是它们的相关度为0。
例2.21 相关性可视化 通过绘制对应属性值对可以很容易地判定两个数据对象x和y之间的相关性。
2.4.6 邻近度计算问题
本节讨论与邻近性度量有关的一些重要问题:(1)当属性具有不同的尺度或相关时如何处理;(2)当对象包含不同类型的属性时如何计算对象之间的邻近度;(3)当属性具有不同的权重时,如何处理邻近度计算。
1. 距离度量的标准化和相关性
距离度量的一个重要问题是当属性具有不同的值域时如何处理。(通常称作“变量具有不同的尺度”)。前面,使用欧几里得距离,基于年龄和收入两个属性来度量人之间的距离。除非这两个属性是标准化的,否则两个人之间的距离将被收入所左右。
一个相关的问题是,除值域不同外,当某些属性之间还相关时,如何计算距离。当属性相关、具有不同的值域、并且数据分布近似于高斯分布时,欧几里得距离的推广,Mahalanobis距离是有用的。具体的说,两个对象x和y之间的Mahalanobis距离定义为:
![]()
其中Σ-1是数据协方差矩阵的逆。注意,协方差矩阵Σ是这样的矩阵,它的第ij个元素是第i个和第j个属性的协方差。
例2.23 在下图中有1000个点,其x属性和y属性的相关度为0.6.在椭圆长轴两端的两个大点之间的欧几里得距离为14.7,但Mahalanobis距离仅为6.实践中,计算Mahalanobis距离的费用昂贵,但是对于其属性相关的对象来说是值得的。如果属性相对来说不相关,只是具有不同的值域,则只需要对变量进行标准化就足够了。
2. 组合异种属性的相似度
前面的相似度定义基于的方法都假定所有属性具有相同类型。当属性具有不同类型时,就需要更一般的方法。直截了当的方法时分别计算出每个属性之间的相似度,然后使用一种导致0和1之间相似度的方法组合这些相似度。总相似度一般定义为所有属性相似度的平均值。
不幸的是,如果某些属性是非对称属性,这种方法效果不好。例如,如果所有的属性都是非对称的二元属性,则相似性度量先归结为简单系数匹配。处理该问题最简单的方法是,如果两个对象在非对称属性上的值都是0,则在计算对象相似度时忽略它们。类似的方法也能很好地处理遗漏值。
算法2.1可以有效地计算具有不同类型属性的两个对象x和y之间的相似度。
3. 使用权值
在前面的大部分讨论中,所有的属性在计算邻近度时都会被同等对待。但是,当某些属性对邻近度的定义比其他属性更重要时,我们并不希望这种同等对待的方法。为了处理这种,可以通过对每个属性的贡献加权来修改邻近度公式。
如果权Wk的和为1,则公式2-15变成:
2.4.7 选取正确的邻近性度量
首先,邻近性度量的类型应当与数据类型相适应。对于许多稠密的、连续的数据,通常使用距离度量,如欧几里得距离等。连续属性之间的邻近度通常用属性值的差来表示,并且距离度量提供了一种将这些差组合到总邻近性度量的良好方法。尽管属性可能有不同的取值范围和不同的重要性,但这些问题通常都可以用前面介绍的方法处理。
对于稀疏数据,常常包含非对称的属性,通常使用忽略0-0匹配的相似性度量。从概念上讲,这反映了如下事实:对于一堆复杂事物,相似度依赖于它们共同具有的性质的数目,而不是依赖于它们所缺失的性质的数目。在特殊的情况下,对于稀疏的、非对称的数据,大部分对象都只有少量被属性描述的性质,因此如果考虑它们都不具有的性质的话,它们都高度相似。余弦、Jaccard和广义Jaccard度量对这类数据是合适的。
在某些情况下,为了得到合适的相似性度量,数据的变换或规范化是重要的,因为这种变换并非总能在邻近性度量中提供。正确地选择邻近性度量可能是一项耗时的任务,需要仔细地考虑领域知识和度量使用的目的。可能需要评估许多不同的相似性度量,以确定哪些结果最有意义。
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第1张图片](http://img.e-com-net.com/image/info8/aaaf1050f79140ab8009512a17ec2335.png)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第2张图片](http://img.e-com-net.com/image/info8/54bd1eaf413749e2a860b46dd3428876.png)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第3张图片](http://img.e-com-net.com/image/info8/66325043a50e47a0b1cac4ceb8adbcf2.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第4张图片](http://img.e-com-net.com/image/info8/39ab4c0a697848d3a41613e30c5e6a94.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第5张图片](http://img.e-com-net.com/image/info8/2f88acfd07cf4c2ea3f07df270082b44.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第6张图片](http://img.e-com-net.com/image/info8/8e61b1d297d644ba846b0e6ca97f4663.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第7张图片](http://img.e-com-net.com/image/info8/8b7423740c32439186b00b4402a5119b.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第8张图片](http://img.e-com-net.com/image/info8/34bb98f0b2694d628a32383fd223a275.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第9张图片](http://img.e-com-net.com/image/info8/6a5ebef66a824c83aa132fa462eac822.png)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第10张图片](http://img.e-com-net.com/image/info8/1703c804a3154d92b5f1142739e3ed5c.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第11张图片](http://img.e-com-net.com/image/info8/2d6a45569dd1468f8e9d56fe7305610d.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第12张图片](http://img.e-com-net.com/image/info8/4ee8cf8b65134b3db5e5793264967b3e.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第13张图片](http://img.e-com-net.com/image/info8/0b36d38d57ec4c21b0681ecef9004a66.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第14张图片](http://img.e-com-net.com/image/info8/bade7d04e2364fdeaae6813d23939ed4.png)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第15张图片](http://img.e-com-net.com/image/info8/a514f858312849b2b089c5ed15f4a372.png)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第16张图片](http://img.e-com-net.com/image/info8/18e0a8ab9fa9499fbe81ea13aecac4cb.jpg)

![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第17张图片](http://img.e-com-net.com/image/info8/6679bfc639444996ba1ff827d3bd067f.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第18张图片](http://img.e-com-net.com/image/info8/dc89d76b968b4c94b3d797434ec4bcda.png)
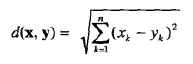
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第19张图片](http://img.e-com-net.com/image/info8/92ebfdf3e9a04bdd94affa30ef3a66c0.png)

![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第20张图片](http://img.e-com-net.com/image/info8/979892d66a65497f93c3eff4df628217.png)
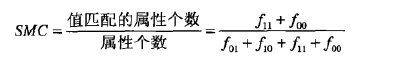

![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第21张图片](http://img.e-com-net.com/image/info8/874ca02a94f24392a017fb2946ec1450.png)

![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第22张图片](http://img.e-com-net.com/image/info8/43fb297a1a0a41cdaa0feaef08839d77.png)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第23张图片](http://img.e-com-net.com/image/info8/941296ee1aff4318b25629dc419f8323.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第24张图片](http://img.e-com-net.com/image/info8/1d603df74100489992fd59d2912474dd.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第25张图片](http://img.e-com-net.com/image/info8/43212cb706aa4a6d90d5a872553eb484.png)
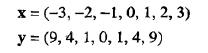
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第26张图片](http://img.e-com-net.com/image/info8/017b424b35304f81b5bef29c99f0e998.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第27张图片](http://img.e-com-net.com/image/info8/f41855f098f346c79bc715394fdd2475.png)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第28张图片](http://img.e-com-net.com/image/info8/590548cd480a44afbbec57878a4c0289.jpg)
![《数据挖掘导论》 - 读书笔记(3) - 数据 [2016-8-13]_第29张图片](http://img.e-com-net.com/image/info8/8acb25ff38b548389e0a07ebd1eb5d7e.jpg)