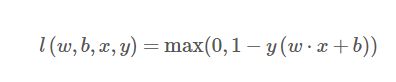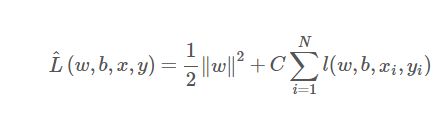机器学习:梯度下降法,几种实现策略
文章目录
- 梯度下降法
- 目标函数:软间隔SVM的目标函数
- 第一种:使用误差最大样本做梯度下降
- 第二种:随机选择一个样本做梯度下降
- 第三种:使用全部样本做梯度
- 第四种:min-batch随机梯度下降
- 第五种:选择top K个误差最大的样本做梯度:
- 第六种:数据归一化和步长自适应,略。
梯度下降法
梯度下降法是求解***无约束最优化问题***的最常见的手段之一。
所以前面提到的软间隔SVM里面转换为hingeloss之后就可以使用梯度下降法实现了。
目标函数:软间隔SVM的目标函数
单个样本的偏导:
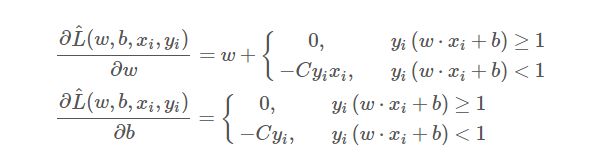
针对上述目标函数,介绍一下几个梯度下降的实现,目的是加深对梯度下降的理解
第一种:使用误差最大样本做梯度下降
首先这种做法是耗时而且有问题的,找出误差最大的样本,需要预测全体样本,耗时,误差最大的样本一般情况下就是噪声,误人子弟。一般启发式算法不会针对单个样本来启发,使用群体来启发,比如某个属性来启发。
import numpy as np
class LinearSVM:
def __init__(self):
self._w = self._b = None
def fit(self, x, y, c=1, lr=0.01, epoch=10000):
x, y = np.asarray(x, np.float32), np.asarray(y, np.float32)
self._w = np.zeros(x.shape[1])
self._b = 0.
for _ in range(epoch):
self._w *= 1 - lr
err = 1 - y * self.predict(x, True)
# 选取误差最大的样本用来更新权值
idx = np.argmax(err)
# 注意即使所有 x, y 都满足 w·x + b >= 1
# 由于损失里面有一个 w 的模长平方
# 所以仍然不能终止训练,只能截断当前的梯度下降
if err[idx] <= 0:
continue
delta = lr * c * y[idx]
self._w += delta * x[idx]
self._b += delta
def predict(self, x, raw=False):
x = np.asarray(x, np.float32)
y_pred = x.dot(self._w) + self._b
if raw:
return y_pred
return np.sign(y_pred).astype(np.float32)
第二种:随机选择一个样本做梯度下降
class LinearSVM_random_one(LinearSVM):
def fit(self, x, y, c=1, lr=0.01, epoch=10000):
x, y = np.asarray(x, np.float32), np.asarray(y, np.float32)
self._w = np.zeros(x.shape[1])
self._b = 0.
for _ in range(epoch):
self._w *= 1 - lr
# 随机选取 1 个样本
batch = np.random.choice(len(x), 1)
x_batch, y_batch = x[batch], y[batch]
err = 1 - y_batch * self.predict(x_batch, True)
# 正确样本,直接再挑选样本
if err <= 0:
continue
# 错误样本,做梯度
delta = lr * c * y_batch
self._w += delta * x_batch
self._b += delta
第三种:使用全部样本做梯度
class LinearSVM_all(LinearSVM):
def fit(self, x, y, c=1, lr=0.01, epoch=10000):
x, y = np.asarray(x, np.float32), np.asarray(y, np.float32)
self._w = np.zeros(x.shape[1])
self._b = 0.
for _ in range(epoch):
self._w *= 1 - lr
# 直接使用全部样本
err = 1 - x * self.predict(y, True)
if np.max(err) <= 0:
continue
# err<0的样本对梯度没作用因为误差为0
mask = err > 0
delta = lr * c * y[mask]
self._w += np.mean(delta[..., None] * y[mask], axis=0)
self._b += np.mean(delta)
第四种:min-batch随机梯度下降
class LinearSVM_minBatch(LinearSVM):
def fit(self, x, y, c=1, lr=0.01, batch_size=128, epoch=10000):
x, y = np.asarray(x, np.float32), np.asarray(y, np.float32)
batch_size = min(batch_size, len(y))
self._w = np.zeros(x.shape[1])
self._b = 0.
for _ in range(epoch):
self._w *= 1 - lr
# 随机选取 batch_size 个样本
batch = np.random.choice(len(x), batch_size)
x_batch, y_batch = x[batch], y[batch]
err = 1 - y_batch * self.predict(x_batch, True)
if np.max(err) <= 0:
continue
mask = err > 0
delta = lr * c * y_batch[mask]
self._w += np.mean(delta[..., None] * x_batch[mask], axis=0)
self._b += np.mean(delta)
第五种:选择top K个误差最大的样本做梯度:
启发式选择,又避免了噪点,但是有一点就是耗时,不见得比minBatch好多少。
class LinearSVM_topK(LinearSVM):
# 用参数 batch_size 表示 Top n 中的 n
def fit(self, x, y, c=1, lr=0.01, topk=128, epoch=10000):
x, y = np.asarray(x, np.float32), np.asarray(y, np.float32)
# 如果 batch_size 设得比样本总数还多、则将其改为样本总数
topk = min(topk, len(y))
self._w = np.zeros(x.shape[1])
self._b = 0.
for _ in range(epoch):
self._w *= 1 - lr
err = 1 - y * self.predict(x, True)
# 利用 argsort 函数直接取出 Top n
# 注意 argsort 的结果是从小到大的,所以要用 [::-1] 把结果翻转一下
batch = np.argsort(err)[-topk:][::-1]
err = err[batch]
if err[0] <= 0:
continue
# 注意这里我们只能利用误分类的样本做梯度下降
# 因为被正确分类的样本处、这一部分的梯度为 0
mask = err > 0
batch = batch[mask]
# 取各梯度平均并做一步梯度下降
delta = lr * c * y[batch]
self._w += np.mean(delta[..., None] * x[batch], axis=0)
self._b += np.mean(delta)