字符串算法:KMP算法+BoyerMoore算法原理及C++实现
前言:
很久以前就写好了字符串搜索的几个经典算法:KMP算法、Boyer-Moore算法以及Rabin-Karp算法。但是一直没有时间写,这次我准备详细的写一下KMP算法,简略的分析下BoyerMoore算法。
原理:
KMP算法:
KMP算法是一种子字符串查找算法,它将会返回目标子字符串在文本中的下标,相比暴力检索算法KMP算法拥有更好的时间复杂度。KMP算法的基本思想
是当字符串出现不匹配的时候,我们就已经知道了一部分的文本内容(即前面以及进行过匹配的文本),我们可以利用这些信息避免检索指针多余的倒退。比如当我们在检索文本"ABABC"中是否存在ABC时,我们检索到第二个"A"时会因为不匹配而停止,若是暴力检索算法,我们会从"B"继续开始检索,但这实际上是没有必要的,因为第一次检索后我们已近直到第二个字符为"B",它并不会进行匹配,所以KMP算法会跳过第二个字符"B"直接从第三个字符"A"开始检索。如图一所示,其中颜色方框表示出现了文本的不匹配。
通过上图,我们可以发现KMP算法可以根据之前的信息,避免文本指针不必要的回退,而要完成这个工作我们最好的方法是使用
确定有限状态自动机(DFA)来完成这个工作。
DFA模拟:
对于KMP算法来说,我们将根据DFA所提供的信息,来完成文本指针的回退。对于每一个文本,它有其确定的一个状态机,如对于"ABABAC"其状态机如图二所示。
而在实际代码中,我们将用二维数组dfa[R][j]来储存状态机(如图三所示),其中R为字典中字符个数,j为模式字符串的长度。
当我们拥有了这个DFA以后,我们即可以开始从文本"ACABABAC"中检索"ABABAC"字符串,当我们在文本中进行检索时,我们将从文本的开头进行检索,同时构造DFA,并使其DFA进入状态0,
我们将依次遍历整个文本,并根据我们检索到的字符来变换状态机的状态,当我们进入6状态后,即完成文本的匹配;若文本检索完成后,仍未进入状态6那么则表示文本中没有相应的子字符串。(如图四所示)
具体代码如下所示:
// 通过dfa来检索子串
int i, j;
for (i = 0, j = 0; i < txt.length() && j < Pat.length(); i++)
j = dfa[txt[i]][j];
if (j == Pat.length())
return i - Pat.length();
else
return txt.length();
可以发现,有了DFA过后,想要在文本中找到我们想要的字符串其实是一件非常简单的事情;但是,
整个KMP算法的难点在我看来就是如何得到DFA,这里有一个非常巧妙但是有一点绕圈的方法来构造DFA,接下来我将结合我的感受对其进行分析;
DFA构造:
DFA的构造我们将使用这样一种方法——通过已构造的DFA来构造后面的DFA,即通过前面的状态来构造后面的状态。在我看来这是非常自然的想法,难点在于我们具体该怎么做。
我们首先会
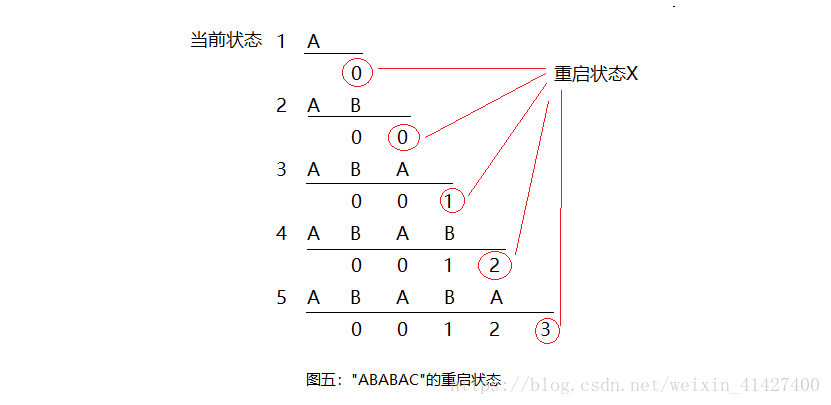
引入一个状态变量X即重启状态,用于记录当我们在某一状态匹配失败时会进入哪一个状态。(如图五所示)这么说可能不是太好理解,举个例子来说,当我们以及匹配完成"ABABA"这五个字符,但是最后一个字符为"B"与"C"匹配失败,那么对于接下来该文本"B"的匹配我们将按照"ABA"时进行匹配处理,那么这时其重启状态X为3,即当此处的字符不是"C"时,我们将按照状态3的情况来处理不匹配的字符串。而我们可以发现,
重启状态总是当前状态之前的状态,这就说明我们通过重启状态使用已构造的状态来生成新的状态。
在构建重启状态时,我们可以通过上图发现,我们不需要构建初始状态(状态0)以及终止状态(状态6)的终止状态,因为这是显而易见的。那么我们该怎么构建它呢?回顾重启状态的定义,
重启状态是当匹配失败时,我们将进入哪一个状态重新匹配以确定其每个字符的对应状态;那么根据这个定义,我们可以发现后面的重启状态可以根据前面的重启状态构建。如上图中的状态5的重启状态,因为4状态时重启状态为2,那么当我们进入状态五时,可以看做当我们在状态4时进行了状态重启进入状态2,状态2中匹配由状态4进入状态5的字符"A"(见图二)使状态2进入了状态3,因此状态5的重启状态X = 3;上面这段话可能有点拗口,但是我觉得是我最好的理解了。因此我们可以发现,
所有的X可以由前一个状态的X所得出,同时状态1的X始终为0,因此我们可以通过递归或者迭代的方法构造DFA。
代码如下:
// 初始化状态机初始指向
dfa[Pat[0]][0] = 1;
for (int i = 1; i < Pat.length(); i++) {
for (int c = 0; c < R; c++)
dfa[c][i] = dfa[c][X];
dfa[Pat[i]][i] = i + 1;
X = dfa[Pat[i]][X]; // 更新下一状态的回溯状态
}
到这里,KMP算法即实现完成。
Boyer-Moore算法:
Boyer-Moore算法与KMP算法相比较简单很多,因此这里只做了简要的分析。Boyer-Moore算法(以下简称BM算法)的原理同KMP有些许类似,也是通过减少模式字符串指针的回退来减少时间复杂度;不过有所不同的是,BM算法是从模式字符串的末尾开始进行检索,若出现不匹配则根据不匹配处的字符进行跳跃。
BM算法中的跳跃主要使用了一个跳跃表Right[C]来储存当字符C不匹配出现时的跳跃长度,其中具体为
字符C在模式字符串即目标子字符串中最右的位置(下标);而对于没有在模式字符串中出现的字符则储存-1。在拥有Right[ ]数组后,我们的处理将会变得很简单,我们
使用一个索引 i在文本中从左向右移动,用另一个索引 j 在模式文本中从又向左移动,判断 j处的字符是否匹配,若不匹配则根据Right[ ]数组将 i下标进行右移,同时重置 j 下标,重新开始新一轮的匹配;直到所有的模式文本匹配完成。最后返回 i 值作为子字符串在文本中的下标。
代码为:
/* BM算法:使用BM算法查找子串
* 参数:txt:用于查找的文本
* 返回值:int:目标字符串首字符在文本中的位置索引
*/
int SubString::BoyerMoore(string txt) {
// 重置跳跃数组
MakeEmpty();
// 构造跳跃数组
// 说明:
// 跳跃数组中Right[char]代表字符char在Pat中最后出现的位置,若Pat中不存在则为-1
Right = new int[R];
for (int i = 0; i < R; i++)
Right[i] = -1;
for (int j = 0; j < Pat.length(); j++)
Right[Pat[j]] = j;
// 通过跳跃数组移动下标索引
int Skip;
for (int i = 0; i < txt.length(); i += Skip) {
// 初始化移动步数
Skip = 0;
for(int j = Pat.length() - 1; j >= 0; j--)
if (Pat[j] != txt[i + j]) {
Skip = j - Right[txt[i + j]];
if (Skip < 1)
Skip = 1;
break;
}
// 当不需要移动时则匹配成功
if (Skip == 0)
return i;
}
return txt.length();
}
/* BM算法:使用BM算法查找子串
* 参数:pat:用于查找的模式字符串,txt:用于查找的文本
* 返回值:int:目标字符串首字符在文本中的位置索引
*/
int SubString::BoyerMoore(string pat, string txt) {
Pat = pat;
return BoyerMoore(txt);
}附录(完整代码 + 额外Rabin-Karp算法代码):
我自己在写的时候,将这些算法都封装到了一个类中,所以第一个将会是他们的声明:
#ifndef SUBSTRING_H
#define SUBSTRING_H
#include
#include
using namespace std;
/* SubString类:
* 接口:
* MakeEmpty:重置功能,重置子串查找器
* KMP:KMP算法,使用KMP算法查找子串
* BoyerMoose:BoyerMoose算法,使用BoyerMoose算法查找子串
* RabinKarp:RabinKarp算法,使用RabinKarp算法查找子串
*/
class SubString
{
public:
// 构造函数
SubString(string pat = "");
// 析构函数
~SubString();
// 接口函数
void MakeEmpty();
int KMP(string txt);
int KMP(string pat, string txt);
int BoyerMoore(string txt);
int BoyerMoore(string pat, string txt);
int RabinKarp(string txt);
int RabinKarp(string Pat, string txt);
private:
// 辅助功能函数
int Hash(string key, int M);
const int R = 256;
string Pat; // 模式字符串
int **dfa; // 储存确定优先状态自动机
int *Right; // 储存跳跃数组
};
#endif // !SUBSTRING_H
接下来是实现文件(.cpp):
#include "SubString.h"
/* 构造函数:初始化对象
* 参数:pat:模式字符串
* 返回值:无
*/
SubString::SubString(string pat) {
Pat = pat;
dfa = NULL;
Right = NULL;
}
/* 析构函数:对象消亡时回收储存空间
* 参数:无
* 返回值:无
*/
SubString::~SubString() {
MakeEmpty();
}
/* 重置函数:重置子串查找器
* 参数:无
* 返回值:无
*/
void SubString::MakeEmpty() {
// 重置确定非限制自动状态机
for (int i = 0; i < R; i++) {
if (dfa != NULL) {
delete dfa[i];
dfa[i] = NULL;
}
}
delete dfa;
dfa = NULL;
// 重置跳跃数组
delete Right;
Right = NULL;
}
/* KMP算法:使用KMP算法查找子串
* 参数:txt:用于查找的文本
* 返回值:int:目标字符串首字符在文本中的位置索引
*/
int SubString::KMP(string txt) {
// 重置状态机
MakeEmpty();
// 申请状态机
dfa = new int*[R];
if (dfa == NULL) {
cout << "自动机申请失败!" << endl;
return NULL;
}
for (int i = 0; i < R; i++) {
dfa[i] = new int[Pat.length()];
for (int j = 0; j < Pat.length(); j++)
dfa[i][j] = 0;
}
// 构造状态机
int X = 0; // 初始化回溯状态
// 初始化状态机初始指向
dfa[Pat[0]][0] = 1;
for (int i = 1; i < Pat.length(); i++) {
for (int c = 0; c < R; c++)
dfa[c][i] = dfa[c][X];
dfa[Pat[i]][i] = i + 1;
X = dfa[Pat[i]][X]; // 更新下一状态的回溯状态
}
// 通过dfa来检索子串
int i, j;
for (i = 0, j = 0; i < txt.length() && j < Pat.length(); i++)
j = dfa[txt[i]][j];
if (j == Pat.length())
return i - Pat.length();
else
return txt.length();
}
/* KMP算法:使用KMP算法查找子串
* 参数:pat:用于查找的模式字符串,txt:用于查找的文本
* 返回值:int:目标字符串首字符在文本中的位置索引
*/
int SubString::KMP(string pat, string txt) {
Pat = pat;
return KMP(txt);
}
/* BM算法:使用BM算法查找子串
* 参数:txt:用于查找的文本
* 返回值:int:目标字符串首字符在文本中的位置索引
*/
int SubString::BoyerMoore(string txt) {
// 重置跳跃数组
MakeEmpty();
// 构造跳跃数组
// 说明:
// 跳跃数组中Right[char]代表字符char在Pat中最后出现的位置,若Pat中不存在则为-1
Right = new int[R];
for (int i = 0; i < R; i++)
Right[i] = -1;
for (int j = 0; j < Pat.length(); j++)
Right[Pat[j]] = j;
// 通过跳跃数组移动下标索引
int Skip;
for (int i = 0; i < txt.length(); i += Skip) {
// 初始化移动步数
Skip = 0;
for(int j = Pat.length() - 1; j >= 0; j--)
if (Pat[j] != txt[i + j]) {
Skip = j - Right[txt[i + j]];
if (Skip < 1)
Skip = 1;
break;
}
// 当不需要移动时则匹配成功
if (Skip == 0)
return i;
}
return txt.length();
}
/* BM算法:使用BM算法查找子串
* 参数:pat:用于查找的模式字符串,txt:用于查找的文本
* 返回值:int:目标字符串首字符在文本中的位置索引
*/
int SubString::BoyerMoore(string pat, string txt) {
Pat = pat;
return BoyerMoore(txt);
}
/* 哈希函数:计算对应字符的Hash数
* 参数:key:想要进行计算的字符串,M:计算的长度
* 返回值:int:目标字符串指定长度的Hash数
*/
int SubString::Hash(string key, int M) {
int h = 0;
for (int i = 0; i < M; i++)
h = R * h + key[i];
return h;
}
/* RK算法:使用RK算法查找子串
* 参数:txt:用于查找的文本
* 返回值:int:目标字符串首字符在文本中的位置索引
*/
int SubString::RabinKarp(string txt) {
// 初始化查找状态
bool Find = false;
int d = 1;
int PLen = Pat.length(), tLen = txt.length(); // 获取模式字符串与文本的长度
int PatHash, txtHash;
// 初始化模式指纹与文本指纹
PatHash = Hash(Pat, PLen);
txtHash = Hash(txt, PLen);
// 获取指纹变换倍数
for (int i = 1; i < PLen; i++)
d *= R;
for (int i = 0; i < tLen - PLen; i++) {
// 比较文本指纹与模式指纹
if (PatHash == txtHash) {
Find = true;
// 比较是否相同
for (int j = 0; j < PLen; j++)
if (txt[i + j] != Pat[j]) {
Find = false;
break;
}
}
else {
// 变化文本指纹
txtHash = (txtHash - txt[i] * d) * R + txt[i + PLen];
Find = false;
}
// 如果查找成功返回对应位置
if (Find)
return i;
}
return tLen;
}
/* RK算法:使用RK算法查找子串
* 参数:pat:用于查找的模式字符串,txt:用于查找的文本
* 返回值:int:目标字符串首字符在文本中的位置索引
*/
int SubString::RabinKarp(string pat, string txt) {
Pat = pat;
return RabinKarp(txt);
}
那么这次的字符串检索算法就结束了,若有什么问题欢迎大家指出~~
转载请标明出处哦~~
参考文献:《算法第四版》