C语言谭浩强第三版第六章例题及课后题:循环控制
| 目录 eg6.2求1-100的加和 eg6.5把100-200之间的不能被3整除的数输出 eg6.6用几个分数来近似pi eg6.7求Fibonacci数列前40个数 eg6.8判断m是否素数 eg6.9求100-200间的全部素数 eg6.10译密码 6.1输入两个正整数m和n,求其最大公约数和最小公倍数 6.2输入一行字符,分别统计出其中英文字母、空格、数字和其他字符的个数 6.4求1!+2!+3!+...+20! 6.5求 1+2+...+100+ 1^2+2^2+...+50^2+ 1/1+1/2+...+1/10 的值 6.6输出所有的水仙花数 6.7编程找出1000之内的所有完数,并按一定格式输出 6.8求一个分数序列的前20项之和 6.9球反弹 6.10猴子吃桃问题 6.11用迭代法求平方根 6.12用牛顿迭代法求方程的根 6.13用二分法求方程的根 6.14输出星星图案 6.15比赛赛手名单匹配 |
eg6.2求1-100的加和
//eg6.2求1-100的加和
/*
//用for循环实现
#include
void main(void){
int i;
int sum = 0;
for(i = 1; i <= 100; i++){
sum+=i;
}
printf("1-100的求和为:%d\n", sum);
}
*/
/*
//用while循环实现
#include
void main(void){
int i = 1;
int sum = 0;
while(i <= 100){
sum+=i;
i++;
}
printf("1-100的求和为:%d\n", sum);
}
*/
//用do while循环实现
#include
void main(void){
int i = 1;
int sum = 0;
do{
sum+=i;
i++;
}while(i <= 100);
printf("1-100的求和为:%d\n", sum);
}
eg6.5把100-200之间的不能被3整除的数输出
break语句只能用于switch语句和循环语句中:
1)在switch语句中,break语句可以使流程跳出switch结构,继续执行switch语句下面的一个语句; 2)在循环语句中,break语句可以用来从循环体内跳出循环体,即提前结束循环,接着执行循环下面的语句。
在没有循环结构的情况下,break不能用在单独的if-else语句中。
在多层循环中,一个break语句只跳出当前循环。
break语句与continue语句的区别是:break是跳出当前整个循环,continue结束本次循环开始下一次循环。
//eg6.5把100-200之间的不能被3整除的数输出
#include
void main(void){
int i;
printf("100-200之间不能被3整除的数有:\n");
/*
//自己
for(i = 100; i <= 200; i++){
if(i%3){
printf("%d ", i);
}
}
*/
//课本 为了说明continue语句的作用
for(i = 100; i <= 200; i++){
if(i%3 == 0){
continue;
}
printf("%d ", i);
}
printf("\n");
} eg6.6用几个分数来近似pi
//eg6.6用几个分数来近似pi
//用pi/4约等于1-1/3+1/5-1/7+...公式求pi的近似值,直到某一项的绝对值小于10^(-6)为止
//i 0 1 2 3
// 1 1/3 1/5 1/7 2i+1
// + - + - 偶数+ 奇数-
//
//课本结果为3.141593 自己运行结果为3.141591
#include
void main(void){
int i = 0;
int m;
double pi = 0;
while(1){
m = 2*i+1;
if((1.0/m) < 1e-6){
break;
}
if(i%2 == 0){ //正号
pi += 4*(1.0/m);
}else{
pi += 4*(-1.0/m);
}
i++;
}
printf("pi的值为:%f\n", pi);
} eg6.7求Fibonacci数列前40个数
//eg6.7求Fibonacci数列前40个数
/*
斐波那契数列指的是这样一个数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,
377,610,987,1597,2584,4181,6765,10946,17711,28657,46368........
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家
列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,
故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……
在数学上,斐波纳契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)
*/
#include
void main(void){
int i = 2;
int sequence[40] = {0}; // int sequence[] = {0}; 错误
sequence[0] = 1;
sequence[1] = 1;
while(i < 40){
sequence[i] = sequence[i-1] + sequence[i-2];
i++;
}
printf("Fibonacci sequence有:\n");
for(i = 0; i < 40; i++){
printf("%-9d ", sequence[i]);
}
printf("\n");
} eg6.8判断m是否素数
//eg6.8判断m是否素数
//质数(prime number)又称素数,有无限个。
//质数定义为在大于1的自然数中,除了1和它本身以外不再有其他因数。
/*
//自己 思路1):判断一个整数m是否是素数,只需把 m 被 2 ~ m-1 (不用判断1)之间的每一个整数去除,如果都不能被整除,那么 m 就是一个素数。
#include
void main(void){
int m;
int i;
int n = 0;
printf("请输入一个正整数:");
scanf("%d", &m);
printf("输入的值为:%d\n", m);
for(i = 0; i < m; i++){
if(m%(i+1) == 0){
n++;
}
}
if(n == 2){
printf("m是素数\n" );
}else{
printf("m不是素数\n");
}
}
*/
// 课本
/* m 不必被 2 ~ m-1 之间的每一个整数去除,只需被 2 ~ 之间的每一个整数去除就可以了。
如果 m 不能被 2 ~ 间任一整数整除,m 必定是素数。例如判别 17 是是否为素数,
只需使 17 被 2~4 之间的每一个整数去除,由于都不能整除,可以判定 17 是素数。
原因:因为如果 m 能被 2 ~ m-1 之间任一整数整除,其二个因子必定有一个小于或等于 ,
另一个大于或等于 。例如 16 能被 2、4、8 整除,16=2*8,2 小于 4,8 大于 4,16=4*4,
4=√16,因此只需判定在 2~4 之间有无因子即可。
*/#include
#include
void main(void){
int m;
int i;
int n = 0;
printf("请输入一个正整数:");
scanf("%d", &m);
printf("输入的值为:%d\n", m);
for(i = 2; i <= sqrt(m); i++){
if(m%i == 0){
n++;
break;
}
}
if(n == 1){
printf("m不是素数\n" );
}else{
printf("m是素数\n");
}
} eg6.9求100-200间的全部素数
//eg6.9求100-200间的全部素数
#include
#include
void main(void){
int m;
int i;
int n = 0; //通过这个值来判断某个数是不是素数
int k = 0; //为了记录素数的个数 也为了控制输出的格式
for(m = 100; m <= 200; m++){
for(i = 2; i <= sqrt(m); i++){
if(m%i == 0){ //不是素数
n++;
break;
}
}
if(i > sqrt(m)){
k++;
printf("%d ", m);
}
if(k % 10 == 0){
printf("\n");
}
n = 0;
}
} eg6.10译密码
如何输入一行字符 不知道个数呀
haha 用getcahr() 学到了 https://mp.csdn.net/postedit/82781637
while((c = getchar()) != '\n'){ }
//eg6.10译密码
//将字母A变成字母E,a变成e,即变成其后的第4个字母,W变成A,X变成B,Y变成C,Z变成D。
//输入一行字符,要求输出其相应的密码
//1.如何输入一行字符 不知道个数呀 haha 用getcahr() 学到了
#include
void main(void){
char c;
printf("请输入一串字符:");
while((c = getchar()) != '\n'){
if((c >= 'A' && c <= 'V') || (c >= 'a' && c <= 'v')){ //前面编程get到的一个方法,这样子即使记不住这些字母的ASCII值也没有关系
c+=4;
}else if((c >= 'W' && c <= 'Z') || (c >= 'w' && c <= 'z')){
c-=22;
}
printf("%c", c) ;
}
} 6.1输入两个正整数m和n,求其最大公约数和最小公倍数
求最大公约数的代码
int gcd(int a, int b){ //他们怎么这么聪明呢,真是太厉害了!
return b == 0 ? a: gcd(b, a%b);
}
//6.1输入两个正整数m和n,求其最大公约数和最小公倍数
//测试:123456 7890 gcd=6
/*
最大公约数 Greatest Common Divisor(GCD)
法1:自己
法2:简化版的 超级简化
最小公倍数(Least Common Multiple,LCM)
法1;依赖于最大公约数
法2:根据自己的定义
*/
/*
a b a mod b
123456 7890 5106
7890 5106 2784
5106 2784 2322
2784 2322 462
2322 462 12
462 12 6
12 6 0
*/
/*
//自己 求最大公因数
#include
void main(void){
int a,b;
int m;
printf("请输入两个正整数:");
scanf("%d%d", &a, &b);
printf("输入的两个正整数为:%d %d\n", a, b);
while((m = a%b) != 0){
a = b;
b = m;
}
printf("最大公约数为:%d\n", b);
}
*/
/*
//网上 百科 求最大公因数
#include
int gcd(int a, int b);
int gcd(int a, int b){ //他们怎么这么聪明呢,真是太厉害了!
return b == 0 ? a: gcd(b, a%b);
}
void main(void){
int a,b;
int m;
printf("请输入两个正整数:");
scanf("%d%d", &a, &b);
printf("输入的两个正整数为:%d %d\n", a, b);
printf("最大公约数为:%d\n", gcd(a, b));
}
*/
/*
//求最大公因数 和最小公倍数
//求最小公倍数法1:利用最大公约数
#include
int gcd(int a, int b);
int lcm(int a, int b);
int lcm(int a, int b){
return a*b/(gcd(a,b));
}
int gcd(int a, int b){ //他们怎么这么聪明呢,真是太厉害了!
return b == 0 ? a: gcd(b, a%b);
}
void main(void){
int a,b;
int m;
printf("请输入两个正整数:");
scanf("%d%d", &a, &b);
printf("输入的两个正整数为:%d %d\n", a, b);
printf("最大公约数为:%d\n最小公倍数为:%d\n", gcd(a, b), lcm(a, b));
}
*/
//求最大公因数 和最小公倍数
//求最小公倍数法2:根据定义进行算法设计。要求任意两个正整数的最小公倍数即,求出一个最小的能同时被两整数整除的自然数。
#include
int gcd(int a, int b);
int lcm(int a, int b);
int lcm(int a, int b){
int i;
for((i = ab? b:a); i <= a*b; i++){ //应该从大数开始,自己搞错了
if(i%a == 0 && i%b == 0){
return i;
}
}
}
int gcd(int a, int b){ //他们怎么这么聪明呢,真是太厉害了!
return b == 0 ? a: gcd(b, a%b);
}
void main(void){
int a,b;
int m;
printf("请输入两个正整数:");
scanf("%d%d", &a, &b);
printf("输入的两个正整数为:%d %d\n", a, b);
printf("最大公约数为:%d\n最小公倍数为:%d\n", gcd(a, b), lcm(a, b));
}
6.2输入一行字符,分别统计出其中英文字母、空格、数字和其他字符的个数
//6.2输入一行字符,分别统计出其中英文字母、空格、数字和其他字符的个数
//My teacher's address is "#123 Beijing Road,Shanghai".
#include
void main(void){
char c;
int english = 0; // 答案用letters
int space = 0;
int number = 0; //答案用digit
int others = 0;
printf("请输入一行字符:");
while((c = getchar()) != '\n') {
if((c >= 'A' && c <= 'Z') || (c >= 'a' && c <= 'z')){
english++;
}else if(c == ' '){
space++;
}else if(c >= '0' && c <= '9'){
number++;
}else{
others++;
}
}
printf("其中英文字母的个数为:%d\n空格数为:%d\n数字数为:%d\n其他字符的个数为:%d\n", english, space, number, others);
} 6.4求1!+2!+3!+...+20!
| 关于阶乘和 matlab执行结果 这两个只是为了验证下面那个函数的正确性 函数factorial(n)可计算阶乘
>> factorial(1)+factorial(2)+factorial(3)+factorial(4)+factorial(5) ans = 153
>> factorial(1)+factorial(2)+factorial(3)+factorial(4)+factorial(5)+factorial(6) ans = 873
>> factorial(20) ans = 2.4329e+18 |
| 注意,此处matlab中输入的内容为: >> f = 0; fprintf('f = %d\n', f);
f = 153为执行的结果
>> f = 0; fprintf('f = %d\n', f);
>>f = 0; fprintf('f = %d\n', f);
>> f = 0; fprintf('f = %d\n', f);
>> f = 0; fprintf('f = %d\n', f);
>> f = 0; fprintf('f = %d\n', f);
>> f = 0; fprintf('f = %d\n', f);
>> f = 0; fprintf('f = %d\n', f); |
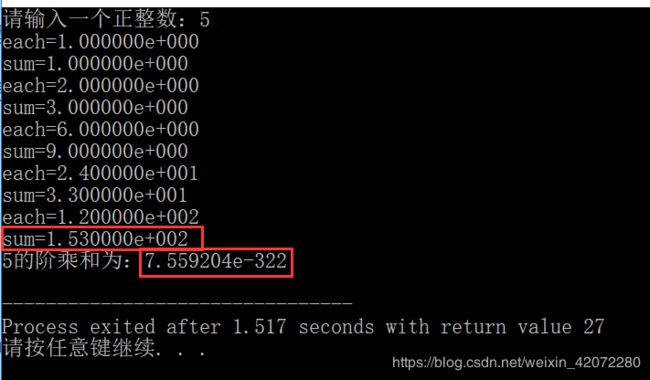
| int型为4个字节,32位,取值范围为:-2^31 ~(2^31-1),即-2147483648 ~ 2147483647 我们发现到n=12时依然可以容纳,但是n=13时已经发生了溢出 所以,此时我们需要修改类型,改为float型,float为4个字节,32位,但其表示的范围为:-3.4*10^(-38) ~ 3.4*10^38,可以容纳得下。 此时需要注意一个问题,就是函数的返回值类型一定要和变量的定义类型一致,如下图,刚开始不一致,出现了下面的结果: 函数里面的sum是一个值,可是传出去就是另外一个值了,究其原因,原来是因为两个类型不一样,
修改了类型之后,结果就正确了,如下。
|
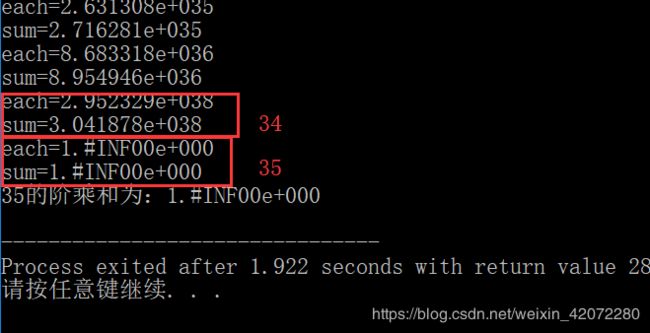
| 下面验证float的范围:float为4个字节,32位,但其表示的范围为:-3.4*10^(-38) ~ 3.4*10^38。
>> factorial(34) ans = 2.9523e+38
>> factorial(35) ans = 1.0333e+40
从上面的运行结果可以看出,34的结果依然可以容纳,35就不行了。 |
//6.4求1!+2!+3!+...+20!
//阶乘(factorial)
#include
float JC(int n);
float JC(int n){ //int JC(int n){
int i;
int j;
float sum = 0; //int sum = 0;
float each; //int each;
for(i = 1; i <= n; i++){
each = 1;
for(j = i; j >0; j--){
each*=j;
}
printf("each=%e\n", each); //printf("each=%d\n", each); //为了debug加入
sum+=each;
printf("sum=%e\n", sum); // printf("sum=%d\n", sum); // 为了debug加入
}
return sum;
}
void main(void){
int n;
printf("请输入一个正整数:");
scanf("%d", &n);
printf("%d的阶乘和为:%e\n", n, JC(n)); //printf("%d的阶乘和为:%d\n", n, JC(n));
} 6.5求 1+2+...+100+ 1^2+2^2+...+50^2+ 1/1+1/2+...+1/10 的值
//6.5求 1+2+...+100+ 1^2+2^2+...+50^2+ 1/1+1/2+...+1/10 的值
#include
void main(void){
int i;
int sum1 = 0;
int sum2 = 0;
float sum3 = 0;
float sum;
for(i = 1; i <= 100; i++){
sum1+=i;
}
for(i = 1; i <= 50; i++){
sum2+=i*i;
}
for(i = 1; i <= 10; i++){
sum3+=1.0/i;
}
sum = sum1+sum2+sum3;
printf("sum1=%d, sum2=%d, sum3=%f, sum=%f\n", sum1, sum2, sum3, sum);
} 6.6输出所有的水仙花数
水仙花数是指一个3位数,其各位数字立方和等于该数本身。
编过好多遍啦,这个就跳过去啦,啦啦啦。
6.7编程找出1000之内的所有完数,并按一定格式输出
//6.7编程找出1000之内的所有完数,并按一定格式输出
//以6为例: 6 its factors are 1,2,3
//一个数如果恰好等于除它以外的因子之和,这个数就称为“完数”
#include
void main(void){
int i, j, k; //循环变量
int a[1000] = {0}; //放某整数的所有因子
int count = 0; //某整数的因子个数
int sum = 0; //除其自身的因子之和
for(i = 1; i < 1000; i++){
for(j = 1; j < i; j++){
if(i%j == 0){
a[count] = j;
count++;
}
}
for(k = 0; k < count; k++){
//printf("各个因子为:%d\n", a[k]); //为了debug
sum+=a[k];
}
//printf("i=%d, sum=%d\n", i, sum); //为了debug
if(i == sum){
printf("%d its factors are ", i);
for(k = 0; k < count; k++){
if(k != count-1){
printf("%d,", a[k]);
}
else{
printf("%d", a[k]);
}
}
printf("\n");
//printf("%d是完数\n", i); //为了debug
}
for(k = 0; k < count; k++){
a[k] = 0;
}
sum = 0;
count = 0;
}
} 6.8求一个分数序列的前20项之和
//6.8求一个分数序列的前20项之和
//2/1 3/2 5/3 8/5 13/8 21/13 …
//numerator 分子
//denominator 分母
//课本答案32.660259 自己答案32.660263
#include
void main(void){
int i = 1;
int numerator = 2;
int denominator = 1;
int tmp;
float each;
float sum = 0;
while(i <= 20){
each = numerator*1.0 / denominator ;
sum+=each;
tmp = numerator;
numerator = numerator+denominator;
denominator = tmp;
i++;
printf("sum=%f\n", sum);
}
} 6.9球反弹
//6.9一个球从100m高度自由落下,每次落地后反跳回原高度的一半,再落下,再反弹。
//求它在第10次落地时,共经过多少米?第10次反弹多高?
#include
void main(void){
float h = 100; //height
float each = h;
float sum = 0;
int i = 1;
while(i <= 10){
sum+=each;
h/=2;
each = h*2;
i++;
}
printf("sum=%f, 第10次反弹%fm\n", sum, h);
} 6.10猴子吃桃问题
//6.10猴子吃桃问题
/*
猴子第一天摘下若干个桃子,当即吃了一半,又多吃了一个。第二天早上又将剩下的桃子吃了一半,又多吃了一个。
以后每天早上都吃了前一天剩下的一半零一个。到第10天早上想再吃时,就只剩一个桃子了。
求第一天共摘多少个桃子?
*/
//答案:1534
#include
void main(void){
int n = 1;
int left;
int i = 9;
while(i>0){
left = n;
n = 2*(left +1);
printf("第%d天有%d个桃子\n", i, n);
i--;
}
} 6.11用迭代法求平方根
//6.11用迭代法求平方根
//求平方根的公式为 x(n+1) = 1/2 * ( x(n) + a/x(n) ),要求前后二次求出的x的差的绝对值小于10^(-5)
#include
#include
void main(void){
float a;
float x = 1;
float tmp;
printf("请输入一个正数:");
scanf("%f", &a);
while(fabs(tmp-x) >= 1e-5){ //while(fabs(tmp-x) < 1e-5){ 刚开始写反了,小傻子
tmp = x;
x = 1.0/2*(tmp + a*1.0/tmp);
}
printf("%f的平方根为:%f\n", a, x);
} 6.12用牛顿迭代法求方程的根
//6.12用牛顿迭代法求方程的根
//求方程 2x^3 - 4x^2 +3x -6 = 0 在1.5附近的根
/*
//自己 只迭代了一次,运行结果为:2.333333
#include
#include
void main(void) {
double x0 = 1.5;
double x1;
double y;
double der; //derivative 导数
y = 2*pow(x0,3) - 4*pow(x0,2) + 3*x0 -6;
der = 6*pow(x0,2) - 8*x0 +3;
x1 = x0 - y/der;
printf("方程在1.5附近的根为:%f\n", x1);
}
*/
//实则 要迭代多次,运行结果为:2.000000 Good job,girl!
#include
#include
void main(void) {
double x0 = 0;
double x1 = 1.5;
double y;
double der; //derivative 导数
while(fabs(x1-x0) >= 1e-5) {
x0 = x1;
y = 2*pow(x0,3) - 4*pow(x0,2) + 3*x0 -6;
der = 6*pow(x0,2) - 8*x0 +3;
x1 = x0 - y*1.0/der;
printf("方程在1.5附近的根为:%f\n", x1);
}
}
6.13用二分法求方程的根
//6.13用二分法求方程的根
//求方程 2x^3 - 4x^2 +3x -6 = 0 在(-10, 10)之间的根
/*
定区间,找中点,中值计算两边看。
同号去,异号算,零点落在异号间。
周而复始怎么办??精确度上来判断。
*/
#include
#include
void main(void){
double xa = -10;
double xb = 10;
double ya;
double yb;
double xm;
double ym;
while(fabs(xa-xb) >= 1e-5){
xm = (xa+xb)/2;
ya = 2*pow(xa,3) - 4*pow(xa,2) + 3*xa -6;
yb = 2*pow(xb,3) - 4*pow(xb,2) + 3*xb -6;
ym = 2*pow(xm,3) - 4*pow(xm,2) + 3*xm -6;
if(ya*ym < 0){ //说明ya和ym异号,说明根在a、m之间
xb = xm;
}else if(yb*ym < 0){
xa = xm;
}
printf("方程根的近似值为:%f\n", xm);
}
}
6.14输出星星图案
//如何按照用户输入的数字输入星星的个数
void star(int n){
int i;
for(i = 0; i < n; i++){
printf("*");
}
}void space(int n){
int i;
for(i = 0; i < n; i++){
printf(" ");
}
}
//6.14输出星星图案
#include
void star(int n){
int i;
for(i = 0; i < n; i++){
printf("*");
}
}
void space(int n){
int i;
for(i = 0; i < n; i++){
printf(" ");
}
}
void main(void){
int i;
for(i = 1; i <= 4; i++){
space(4-i);
star(2*i-1);
printf("\n");
}
for(i = 5; i <= 7; i++){
space(i-4);
star(15-2*i);
printf("\n");
}
}
6.15比赛赛手名单匹配
//思路:需要每次的X Y Z各出现且仅出现一次 ,如何实现呢? 见下面,神奇!
#includevoid main(void){
char i;
char j;
char k;
for(i = 'X'; i <= 'Z'; i++){
for(j = 'X'; j <= 'Z'; j++){
if(i!=j){
for(k = 'X'; k <= 'Z'; k++){
if(k!=i && k!=j){
printf("A=%c, B=%c, C=%c\n", i, j, k);
}
}
}
}
}
}
//6.15比赛赛手名单匹配
/*
两个乒乓球队进行比赛,各出3人。甲队为ABC三人,乙队为XYZ三人。已抽签决定比赛名单。有人向队员打听比赛的名单,
A说他不和X比,C说他不和X、Z比,请编程序找出3对赛手的名单。
*/
/*
//自己的 错误 瞎搞
#include
void main(void){
char i;
char j;
for(i = 'A'; i <= 'C'; i++){
for(j = 'X'; j <= 'Z'; j++){
if((i == 'A' && j == 'X') || (i == 'C' && j == 'X') || (i == 'C' && j == 'Z')){
continue;
}else{
break;
}
}
printf("i=%c, j=%c\n", i, j);
}
}
*/
//思路:需要每次的X Y Z各出现且仅出现一次 ,如何实现呢?
//再把条件加进去,就OK啦!
#include
void main(void){
char i;
char j;
char k;
for(i = 'X'; i <= 'Z'; i++){
for(j = 'X'; j <= 'Z'; j++){
if(i!=j){
for(k = 'X'; k <= 'Z'; k++){
if(k!=i && k!=j){
if(i!='X' && k!='X' && k!='Z'){
printf("A=%c, B=%c, C=%c\n", i, j, k);
}
}
}
}
}
}
}