计算机导论与C语言基础 Coursera 第七周

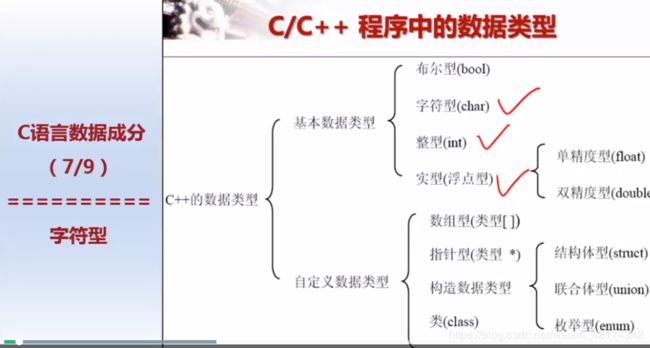
第七周

1 明确学习进度

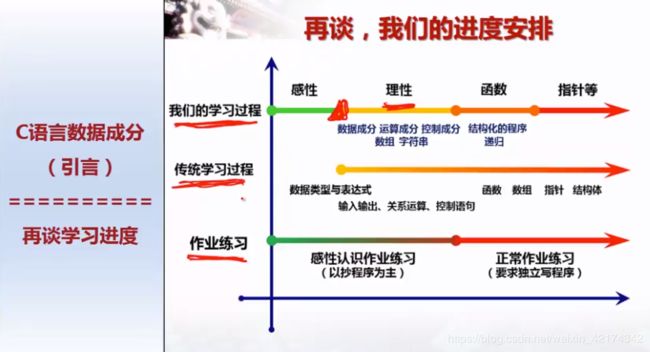
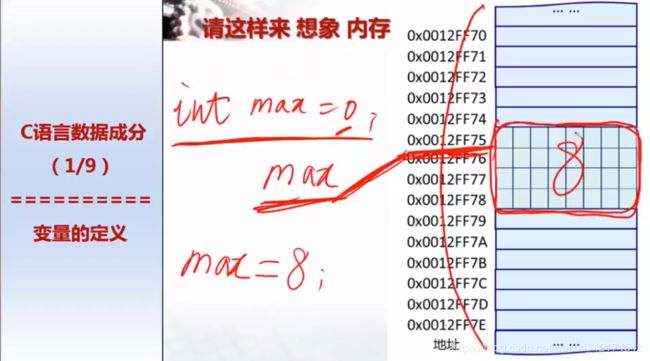
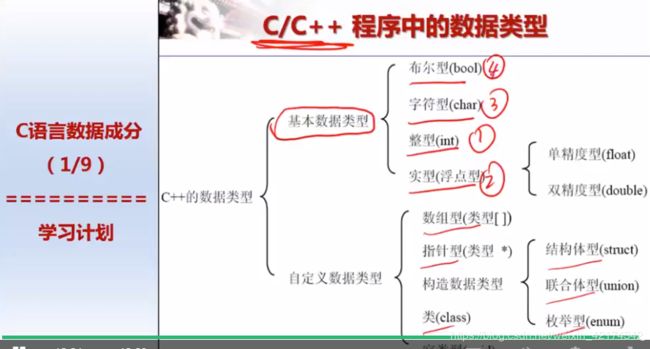
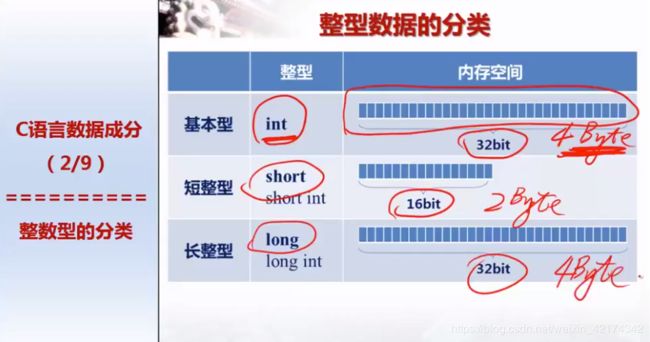
以上的情况是VC编译环境中的数据。每个编译环境对这些解释不通。主要是因为C标准问题。

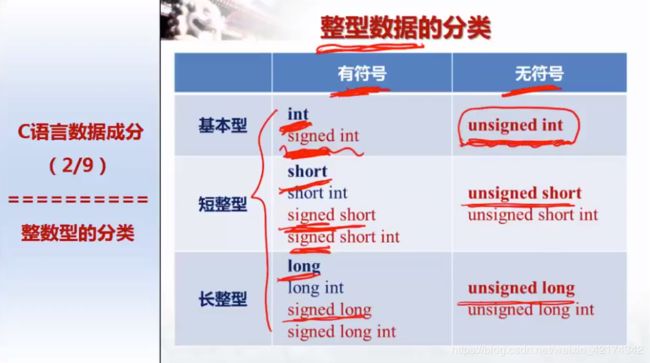
2 整数

这种储存结构在组成原理中会讲，大概意思就是这种方式会使计算加快。

hex控制输出打印符。


输出控制符必须要切回来。


0x代表16进制 0代表8进制

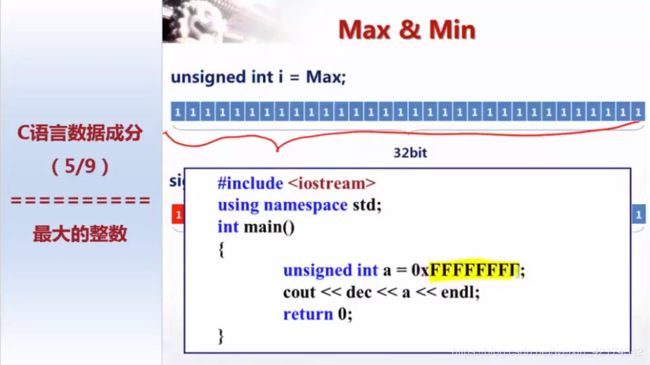
int最大大约在42亿。


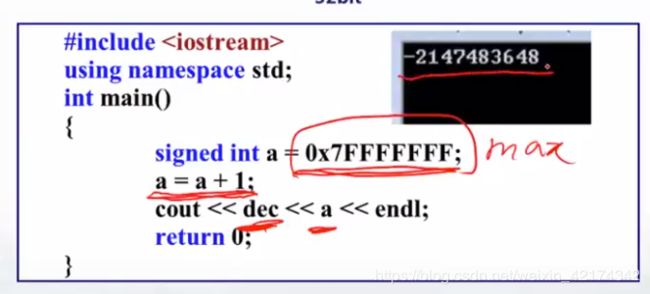
最大的数+1 就变成最小的数了。

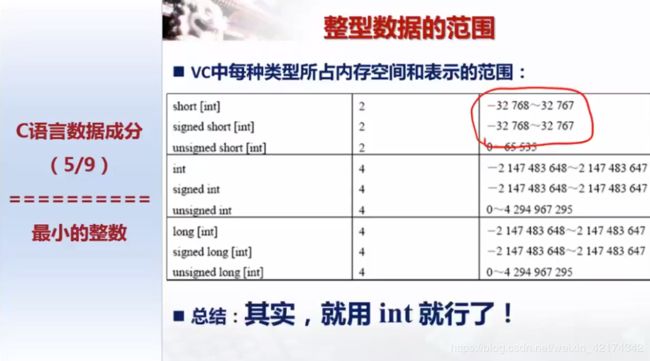
3其他类型

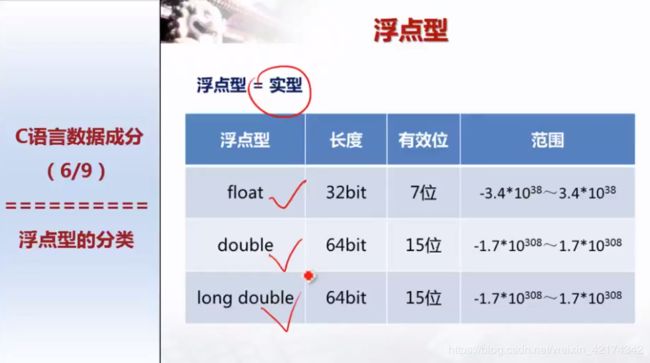
float精度只有7位。

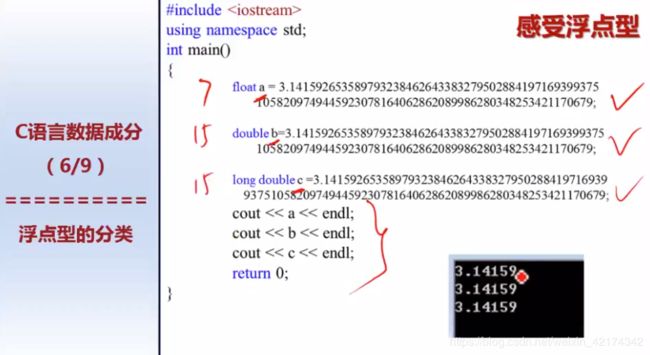
cout默认打印6位精度。

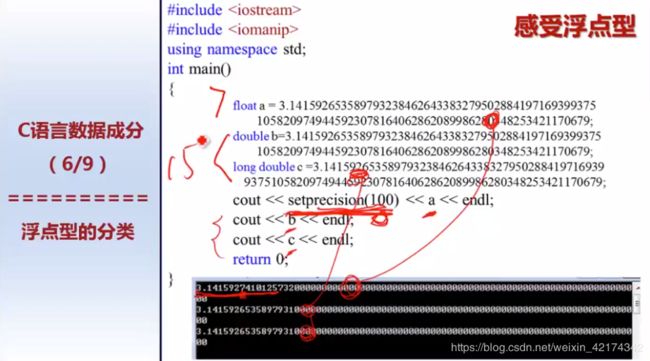
浮点型的表示方式。

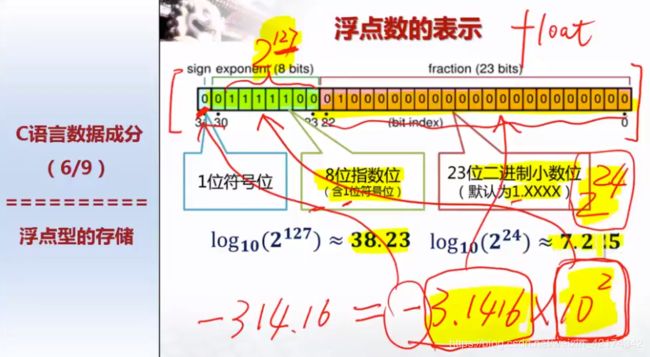
浮点表示法是已知的C/C++编译器都是按照IEEE（国际电子电器工程师协会）制定的IEEE浮点数表示法来进行运算的。这种结构是一种科学表示法，用符号（+或-）、指数和尾数来表示，底数被确定为2。所以在IEEE浮点数表示法里，一个浮点数为尾数乘以2的指数次方再加上符号。
这边是组成原理的部分





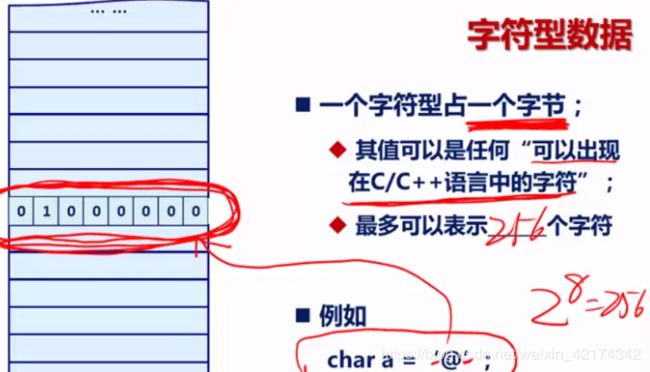
字符型必须是单引号，双引号是字符串



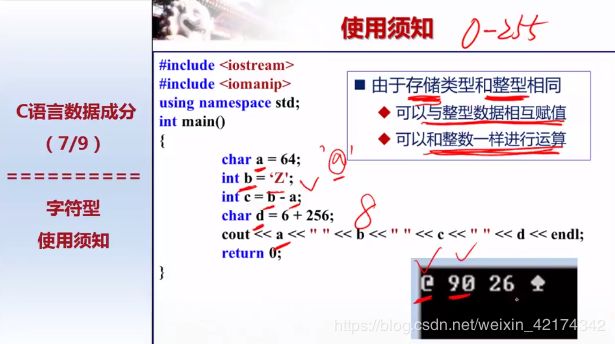
超出之后就出现截断现象。

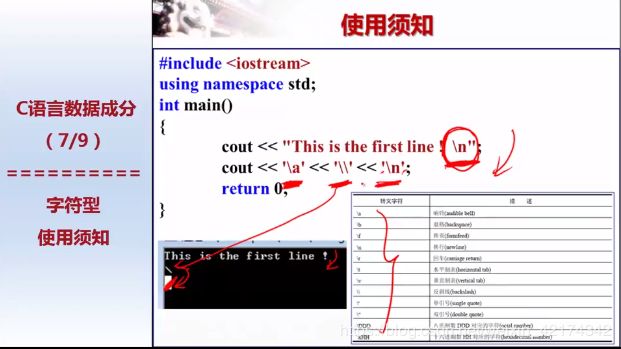
转义字符

const 在前面标注
定义后在程序中不能被改变数值




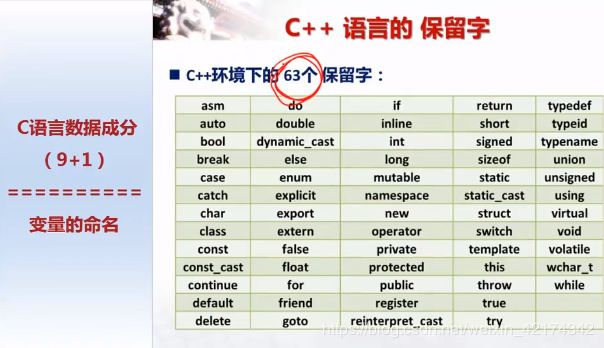
这边是Ｃ＋＋中保留字符

4 作业

//http://pkuic.openjudge.cn/hw03/1/
//编程题＃1：年龄与疾病
//来源 : POJ(Coursera声明：在POJ上完成的习题将不会计入Coursera的最后成绩。)
//
//	 注意： 总时间限制 : 1000ms 内存限制 : 65536kB
//
//	 描述
//	 某医院想统计一下某项疾病的获得与否与年龄是否有关，需要对以前的诊断记录进行整理。
//
//	 输入
//	 共2行，第一行为过往病人的数目n（0 < n <= 100)，第二行为每个病人患病时的年龄。
//
//	 输出
//	 每个年龄段（分四段：18以下，19 - 35，36 - 60，大于60注意看样例输出的格式）的患病人数占总患病人数的比例，以百分比的形式输出，精确到小数点后两位（double）。关于c++的格式化的输入输出，请参考：http://www.cplusplus.com/reference/iomanip。也可以在网上搜索一下，资料很多的。
//
//样例输入
//10
//1 11 21 31 41 51 61 71 81 91
//样例输出
//1 - 18: 20.00 %
//19 - 35 : 20.00 %
//36 - 60 : 20.00 %
//60 - : 40.00%

//提示
//注意最后一行的输出是“60 - : ”，而不是“61 - : ”。
//
//每个冒号之后有一个空格。
//
//输出可以用 cout << fixed << setprecision(2) << f; 来保留f后面的两位小数。

#include      // std::cout, std::fixed
#include       // std::setprecision
using namespace std;

int main(){
	int n;
	cin >> n;
	int a[100];

	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}

	int Num0118=0, Num1935=0, Num3660=0, Num60=0;

	for (int i = 0; i < n; i++)
	{
		if (a[i]<=18)
		{
			Num0118 += 1 ;
		}
		else if (a[i]<=35)
		{
			Num1935 += 1;
		}
		else if (a[i] <= 60)
		{
			Num3660 += 1;
		}
		else{
			Num60 += 1;
		}
	}
	cout << "1-18: " << fixed << setprecision(2) << double(Num0118*100/n)<<'%'<

double()命令用法出错

#include      // std::cout, std::fixed
#include       // std::setprecision
using namespace std;

int main(){
	int n;
	cin >> n;
	int a[100];

	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}

	int Num0118=0, Num1935=0, Num3660=0, Num60=0;

	for (int i = 0; i < n; i++)
	{
		if (a[i]<=18)
		{
			Num0118 += 1 ;
		}
		else if (a[i]<=35)
		{
			Num1935 += 1;
		}
		else if (a[i] <= 60)
		{
			Num3660 += 1;
		}
		else{
			Num60 += 1;
		}
	}
	cout << "1-18: " << fixed << setprecision(2) << (double(Num0118)*100/n)<<'%'<

//http://pkuic.openjudge.cn/hw03/2/
//编程题＃2：成绩判断
//来源 : POJ(Coursera声明：在POJ上完成的习题将不会计入Coursera的最后成绩。)
//
//	 注意： 总时间限制 : 1000ms 内存限制 : 6000kB
//
//	 描述
//	 输入一个0--100的分数，判断分数代表什么等级。
//
//	 95 <= 分数 <= 100, 输出1
//
//	 90 <= 分数<95, 输出2
//
//	 85 <= 分数<90, 输出3
//
//	 80 <= 分数<85, 输出4
//
//	 70 <= 分数<80, 输出5
//
//	 60 <= 分数<70输出6
//
//	 分数 < 60; 输出7.
//
//	 输入
//	 n
//
//	 输出
//	 m
//
//	 样例输入 87 

//样例输出 3

#include 
using namespace std;

int main(){
	int score;
	cin >> score;

	if (score<60)
	{
		cout << 7 << endl;
	}
	else if (score<70)
	{
		cout << 6 << endl;
	}
	else if (score<80)
	{
		cout << 5 << endl;
	}
	else if (score<85)
	{
		cout << 4 << endl;
	}
	else if (score<90)
	{
		cout << 3 << endl;
	}
	else if (score<95)
	{
		cout << 2 << endl;
	}
	else
	{
		cout << 1 << endl;
	}

	return 0;
}

//http://pkuic.openjudge.cn/hw03/5/
//编程题＃4：人民币支付
//来源 : POJ(Coursera声明：在POJ上完成的习题将不会计入Coursera的最后成绩。)
//
//	 注意： 总时间限制 : 1000ms 内存限制 : 65536kB
//
//	 描述
//	 从键盘输入一指定金额（以元为单位，如345），然后输出支付该金额的各种面额的人民币数量，显示100元，50元，20元，10元，5元，1元各多少张，要求尽量使用大面额的钞票。
//
//	 输入
//	 一个小于1000的正整数。
//
//	 输出
//	 输出分行，每行显示一个整数，从上到下分别表示100元，50元，20元，10元，5元，1元人民币的张数
//
//	 样例输入  735
//	 样例输出
//7
//0
//1
//1
//1
//0

#include 
using namespace std;

int main(){
	int price;
	cin >> price;
	int money[6] = {100,50,20,10,5,1};

	for (int i = 0; i < 6; i++)
	{
		cout << price / money[i]<

////http://pkuic.openjudge.cn/hw03/3/
//编程题＃3：找出第k大的数
//来源 : POJ(Coursera声明：在POJ上完成的习题将不会计入Coursera的最后成绩。)
//
//	 注意： 总时间限制 : 1000ms 内存限制 : 65536kB
//
//	 描述
//	 用户输入N和K，然后接着输入N个正整数（无序的），程序在不对N个整数排序的情况下，找出第K大的数。注意，第K大的数意味着从大到小排在第K位的数。
//
//	 输入
//	 N
//
//	 K
//
//	 a1 a2 a3 a4 .....aN
//
//	 输出
//	 b
//
//	 样例输入
//5
//2
//32 3 12 5 89
//
//样例输出
//32

//提示
//这是一道很经典的算法问题，是公司面试的常见考题。以后学习递归之后再回头看看这道题，或许有新解法。
//参考
//https://www.cnblogs.com/fengkang1008/p/4727038.html

#include 
using namespace std;

//冒泡算法
//int main(){
//	int N, K;
//	cin >> N >> K;
//	int a[100];
//	for (int i = 0; i < N; i++)
//	{
//		cin >> a[i];
//	}
//	for (int i = 0; i < K; i++)
//	{
//		for (int j = N-1; j >i; j--)
//		{
//			if (a[j] > a[j - 1]){
//				int temp = a[j];
//				a[j] = a[j - 1];
//				a[j - 1] = temp;
//			}
//		}
//	}
//	cout << a[K-1]<< endl;
//
//	return 0;
//}

//快排算法
int main(){
	int N, K;
	cin >> N >> K;
	int a[100];
	for (int i = 0; i < N; i++)
	{
		cin >> a[i];
	}
	
	for (int i = 0; i < K; i++)
	{
		int maxIndex = i;
		for (int j = i+1; j < N; j++)
		{
			if (a[maxIndex] < a[j]){
				maxIndex = j;
			}
		}

		if (maxIndex != i){
			int temp = a[i];
			a[i] = a[maxIndex];
			a[maxIndex] = temp;
		}
	}
	cout << a[K - 1] << endl;
	return 0;
}