Lec2 Array and Linked List Textbook Ch 10.2Array and Linked List Textbook Ch 10.2

• List ADT
• Array
• Linked list
• Doubly linked list
• Node-based storage with arrays

怎么把一直在变化的ai传入
Method 1: array：对稀疏数组浪费太大
Method 2: structure array：the coefficient ??, the index no. ?.
按照系数降/升序存储：有利于多项式相加（升序要多加一个标准判断是否到头）

所谓抽象类型实际上包括了两个要素
一是这个类型所包含的数据对象集是什么：
对线性表来说，他的对象集是由n个元素组成的一个有序序列（元素具体类型 随意）
二是operation

An Abstract List (or List ADT) is linearly ordered data (通常with same data type)有序线性
由同类型数据元素构成有序序列的线性结构
表中元素个数为线性表的长度
线性表没有元素时，称为空表 empty List
表起始位置称为表头List head，表结束位置称为表尾List tail

List ADT 顺序存储

元素上相邻物理位置上相邻-可用一维结构表示二维信息index=位置
需要申请内存——知道有多长MAXSIZE，已经存了多少Last
Insert、Delete：从最后/最前一个开始挪动位置，时间复杂度O(n)

Linked list链式存储（单向列表）

object is stored in a node：包含reference/pointer、data
物理地址不再相连：insert erase方便很多

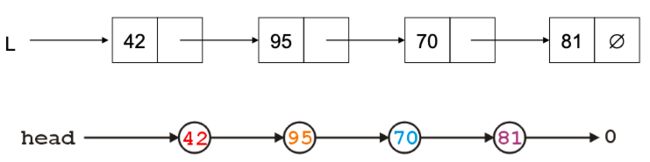
需要一个表头L，最后一个node的指针域pointer为null

class Node {
		# 包含data和ptr
        private:
			int element; 
            Node *next_node;
		public:
			Node( int = 0, Node * = nullptr );
            int retrieve() const;
            Node *next() const;
    };

长度不受限制，否则再加一个数组不能保证相连
Node Constructor

Node::Node( int e, Node *n ): element( e ),
next_node( n ) {
         // empty constructor
     }
     
Node( int = 0, Node * = nullptr );

Accessors

int Node::retrieve() const {
         return element;
     }
Node *Node::next() const { return next_node;
}

Linked List Class

class List {
         private:
Node *list_head; // ...
};

Structure
Operations
在删除时必须释放node
只讨论头节点（只有ptr）
int e = front();拿出这个节点的数据
需要新定义零时ptr存储node数据和指向
重新指向
删除指针

只能往后插入，要往前只需要交换data——其他改进方法（付出空间代价）
好处

多变量多项式的存储结构（广义表/多重链表）：首先化简为y的多项式*x的高次项，形成Ax^n的结构，嵌套链表，A也为链表，Ax同样为链表。data上也可以是链表

后面：两个链表的融合、用数组表达？