二值化网络的发展——从原始BNN到MeliusNet

二值化网络的发展

一.开山之作——Binarized Neural Networks

本文题目为《Binarized Neural Networks: Training Neural Networks with Weights and Activations Constrained to +1 or −1》

文章主要建设性内容

本文提出了一种新的轻量级网络——二值化网络。二值化网络即将网络中权重固定为-1和+1两个值，feather map也要进行二值化处理。从空间角度来看，原先保存的权重都是32bit的浮点数，现在变成了1bit的精度，节省了32倍的储存空间；从时间角度来看，+1与-1之间的乘法运算可以利用同或运算代替，这可以大大的提高运算速度，同时利用popcount操作代替加法，进而实现对卷积操作的提速。
实现这种1bit量化的方法有两种，统计法或者确定法。统计法（stochastic）使数学期望连续，而确定法则是直接利用符号函数sign进行量化。为了方便硬件并且加速，选择确定法进行量化，并且在之后的各种二值化网络中，无一例外的都采用了确定法进行二值化量化。
由于采用这样的量化方法就会对梯度的反向传播造成一个问题，sign函数在非零的地方导数为0，在零处又不可导。因此采用叫做staight-through estimator(STE)方法，即反向传播时利用Htanh代替原先激活函数sign进行求导，可以保证梯度可以顺利传播。与此同时，更新参数时，保存的权重是浮点类型，每次更新一点，累计达到符号改变则会改变量化时的值，但是前向传播计算的时候，利用的权重是二值化的。这一个方法也是在之后二值化网络中被广泛采用的。
由于输入层计算量小且信息稠密，没有对第一层的输入采取量化。作者同时提出了一个很巧妙的方法，由于输入的图像每个像素点都是8bit的，因此可以把每一个bit拆开，相当于把3通道的8bit图像看做一个24通道的1bit图像，这样既不损失信息，也可以利用二值化的巧妙同或运算代替乘法提速。在之后的网络中，为了保证精度，都会在一些特殊的地方采用全精度浮点运算，在少量增加计算量的代价下，尽可能减少二值化带来的信息损失。
BN操作，为了提高运算速度，文章采用了利用移位代替乘法的操作。这种名叫SBN的方法，是很粗糙的，把bn中的乘法除法全用最近的二的几次方进行近似，因为可以用移位操作来替换。文章中说这个方法对于精度几乎没有影响，但是我看这个对于计算的近似实在是相当的粗糙。不过，由于本身网络就是二值化的，可能即使bn计算的粗糙，但是二值化网络对于中间层的输出并没有太高的精度要求，反正都要进行sign函数的量化处理。因此我认为，这SBN的方法是可以在实际应用中用上的。
由于权重是二值化的，也就意味一个3x3的卷积核只有512种不同可能，因此可以把权重相同的卷积核放到同一个地址，进而大大减小存储。这个特点是二值化网络特有的优势。

文章的缺点

由于这篇文章作为BNN的开山之作，BNN网络的精度是很差是可以谅解的。这篇文章中几乎把所有可以进行提速的操作全进行了提速。比如把BN换位SBN，把Adam优化器也进行了改变。SBN的问题之前已经说过，若对准确率无影响那确实是可取的。但是对于文章中的对优化器做改变，把参数设置的恰好可以用移位操作代替乘除操作，这是会影响到训练的效果与训练的时长的。其次，一个二值化网络主要是要训练好之后再部署到轻量的硬件上进行使用，一般都是在GPU上训练，训练时这种小trick可能会提速但并不是很有必要，若影响结果就丢了西瓜捡芝麻了。

提出的想法

本文提出的是量化的方法，而不是网络的结构。作者做的实验是针对于原先提出的简易的网络的，但是显然BNN这种特殊的处理方法应该有更符合其特点的网络结构。我认为之后对于BNN基本上是两个研究思路，一个是研究更符合BNN的model结构，另一个思路是在量化方法上做一些trick。之后的MeliusNet就是模型结构上的改进，而IRNet则是一种量化与训练方法上的改进。

二. XNOR-Net

本文题目为《XNOR-Net:ImageNetClassificationUsingBinary ConvolutionalNeuralNetworks》

文章主要建设性内容

本文与BNN提出时间接近，都属于二值化网络的基石。本文将BNN网络分为两种，一种是单纯权重二值化，一种是权重与输入均二值化。我认为单纯权重二值化在参数的存取上节省了大量的空间，但是在加速模型推理时间上并没有很大的提升。因为输入与权重同时二值化才可以带来利用xnor与popcount代替卷积操作的加速效果，对于运算提升效果显著。
本文第一个亮点在于提出了一个“伸缩因子”的参数，利用绝对值取平均的方式，保证二值化卷积运算过后得到的值，与没有二值化时得到的准确结果尽可能的相近，并且进行了证明。这个思路还是很好的，可以大大的提高计算的精度，并与此同时保留了二值化网络卷积计算的加速功能。我认为，这种利用伸缩因子以达到运算结果尽可能接近全精度计算的结果的方法是一个好的方法和思路，在我之后看到的BNN文章中基本上都用了这种方法。关于伸缩因子的计算，文章还提到了一种能够减少重复运算的方法，确实是很巧妙也值得借鉴的。
本文还有一个亮点在于提出了适用于二值化网络的卷积结构。

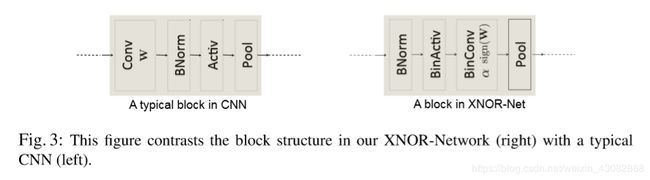
不同于全精度的网络的卷积结构，先卷积后bn，之后经过激活函数，再池化下采样。适用于二值化网络的结构应该是在二值化之前进行BN操作，这样可以减少二值化量化带来的损失，因为这可以保证值分布在0附近。如若需要加入pool实现下采样，pool操作要放到卷积后而不是二值化后，因为二值化后结果只有+1与-1，maxpool后很可能得到的几乎全是1，严重损失了信息。

文章的缺点

首先，最重要的问题是此网络精度仍然很差。
文章中提出的只量化weight的网络比较鸡肋，确实可以减少参数储存空间，但是精度损失的代价与回报不成比例。
文章中提到了激活函数，如图
我认为在已经利用了二值化网络量化的条件下，激活函数并不需要再加上了。因为激活函数的本质是为了使网络非线性化，已经利用sign进行了二值化量化了，再加入激活函数会使损失的信息过多了，不利于精度的提高。

提出的想法

文章中伸缩因子的提出其实表明了一个目的，或者说一种思想，即：二值化网络是对于全精度网络的一种近似表示，从参数到运算都要尽可能的接近全精度网络的参数与计算结果。但是我认为这种思想是不完全正确的，应该意识到，二值化网络是一种完全特殊的网络，与8bit量化不同，二值化网络并不是对于全精度网络的近似。因此，从结构上应该与普通神经网络有所区别，不应该套用完全相同结构，而是应该有适合于二值化网络的结构。
我认为在BNN论文中对于第一层网络的处理是符合这个思路的，值得借鉴的。不过暂时我还没有找到好的办法。
在IRNet中那种利用信息熵与伸缩因子相结合的方法是非常非常巧妙的。

三.BinaryDenseNet

本文题目为《Back to Simplicity: How to Train Accurate BNNs from Scratch?》

本文主要建设性内容

这篇文章是比较新的文章了，在2019年6月完成的。本文回顾了之前的各种二值化网络并提出了一些设计二值化网络的原则，并提出了新的结构BinaryDenseNet。
本文在简介中提到，之前大量的二值化网络把重心放到了减少量化带来的损失，采用了如加入伸缩因子、预训练等等方法。使用的结构也是全精度浮点网络的经典结构如AlexNet，ResNet等。但是这些结构并不一定适用于二值化网络，这与之前我提到的想法不谋而合，二值化网络有自身的特点，应该有特殊的网络结构。
本文对于之前的一些提高准确率的办法进行了分析并给出了经验上的证明。主要提出三点内容：scaling factor没有意义（这一点我是否定的，见后文“文章的缺点”部分）；在全精度网络基础上进行fine-tuning是没有意义的；approxsign只对于fine-tuning有特殊意义，因此也没有必要应用。
文章提出了几条BNN的黄金准则：
1.保证网络中丰富的信息流是提高准确率的关键。
2.不是所有好的全精度网络结构都适合应用在二值化网络上，轻量级网络的信息冗余是比较少的，因此无法利用冗余的信息来补偿量化造成的精度损失。
3.全精度下采样要谨慎，会严重损失信息。
4.跳跃链接shortcut是很重要的，有利于避免信息流中的瓶颈。
5.为了克服信息流中的瓶颈，可以增加网络的宽度与深度，但是会增加计算。
6.之前的策略如scaling factor、approxsign、预训练等是不必要的
同时，文章提出了建议：
1.尽可能的使用更多的跳跃链接shortcut
2.少用瓶颈层，但是由于瓶颈层的使用可以减少卷积核。因此应该找到一个良好的权衡。
3.关键层要用全精度浮点运算。输入层、输出层与下采样层最好使用全精度。其次，虽然下采样层可以减小feather-map的size，但是还是要谨慎使用，因为信息损失太多了。
文章提出了一种结构 BinaryDenseNet，在DenseNet的基础上进行改进，将瓶颈层改为了3x3的卷积。结构如下：

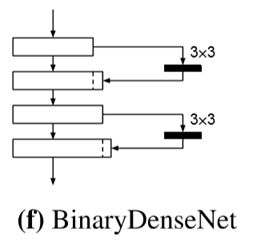
提出一个参数叫做growth rate，也就是连接到下一层的通道数，即每一层新增的通道数。作者认为提高网络的深度，减少growth rate是有利于减少信息损失的。实验如下：

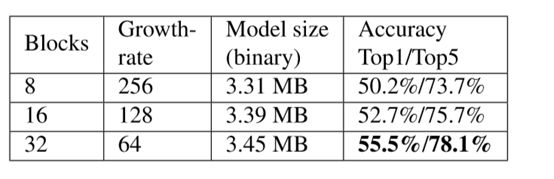
对于下采样，BDN的下采样同时要减少通道的数量。为了保证信息，有两种方式，一种是采用全精度，一种是采用二值化下采样但是同时就不减小通道数量了。对于全精度下采样，提出了一种结构：

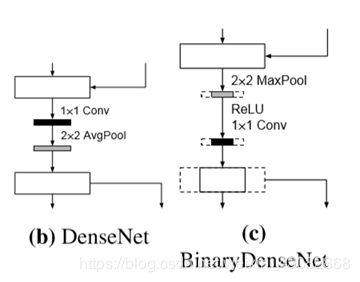
利用Maxpool–Relu–1x1Conv的顺序代替原有顺序，有利于减少运算量。

文章的缺点

文章对“伸缩因子”（scaling factor）提出了否定的态度，并举出了实验数据证明伸缩因子没有使准确率提高。文章认为在卷积之后加入BN的操作会吸收掉伸缩因子带来的影响，导致准确率不增反降。然而，在XNOR的文章中明确提出了对于二值化网络而言，BN层应该放到卷积之前而不是卷积之后。如果按照XNOR的方法，伸缩因子的效果提升就不会被BN吸收掉了，应该是有积极影响的。

四.MeliusNet——达到MobileNet精度的二值化网络

本文名为《MeliusNet: CanBinaryNeuralNetworksAchieveMobileNet-levelAccuracy?》这是一篇很新的文章，2020年刚出的。

本文主要建设性内容

本文主要在说如何改善二值化网络中feature map的低质量与低容量。我理解文章中所谓的质量与容量的意思分别对应的是二值化weight与二值化input。
作者利用Improvement Block增加质量，利用Dense Block增加容量。具体结构如下图：

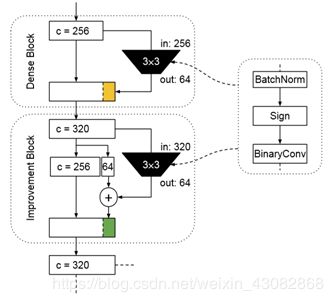
注意到，这里面的卷积结构是先进行BN后量化，然后进行卷积操作，与Xnor中提出的结构相同。
由于Dense Block会增加通道数，因此需要有适当的下采样部分对weight,height,channel进行降低。完整网络的结构如下：

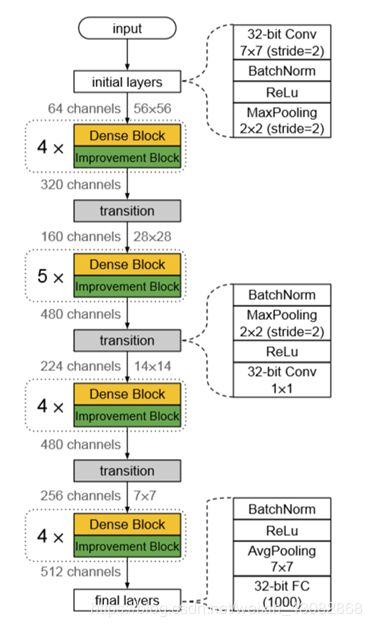
为了减少信息的流失，根据之前文章的启发，对于第一层与最后一层采用全精度，对于下采样层也就是其中的1x1卷积层采用全精度。
文章还通过做实验证明这样的网络结构是特殊的适用于二值化网络，且将全精度32位的参数量相近的MeliusNet与DenseNet进行对比发现其实现的准确率几乎一致，而二值化的两种网络MeliusNet有更好的表现。
文章为了减小浮点运算量，将第一层的7x7卷积替换为了3个3x3的卷积，并且得到了更好的效果。并且利用组卷积降低计算量，下采样卷积若想用组卷积还加入了shuffle操作。

文章的缺点

文章对于容量与质量的提法让人耳目一新，但是之后对于两个概念并没有深究下去。为什么Improvement Block增加质量，利用Dense Block增加容量，这很迷。很好理解的是他们保留了input的原始信息，但是这只是capacity层面的。Improvement Block这样的结构并没有保留更多的weight信息，因此不能理解这是如何提高的quality。
对于文章提出的结构有点质疑，这种结构可能只是凑巧的效果还不错，但是总体来说，这篇文章没有BDN那篇文章对于原理讲的那么清晰，应该按照BDN文章的思路走，去探索具有更好的效果的结构。

提出的想法

对于这里Dense和Improvement为什么要采用这样的结构，我有些自己的想法。注意到，这里面的主体部分其实是一直没有变的。以此图为例，

这里面前256个通道的值，输入与输出前后都没有发生改变，变化的只是增加的64个通道的值，可以认为这64个通道是对于前256个通道的特征的一个提取。这种方式所保证的就是信息的无损失，每次卷积运算获得的是新提取得到的信息。
第一层提出要用3个3x3卷积代替原先的7x7卷积，并且利用组卷积降低计算量。可不可以用更少的3x3卷积去代替？可不可以利用深度可分离卷积去代替组卷积？这可以更大的降低运算量。
文中全精度浮点运算可以利用8bit量化来代替吗？这样可以减小大量的参数量，并且带来的信息损失不是很多。不过我担心对于这种二值化网络，8bit量化造成的损失会非常严重，这需要实验去检验。

保留的疑问

本文最大的疑问就是为什么第一层要用7x7如此巨大的卷积层，这是ResNet一开始提出时的东西，但是作为以减小运算量为目的的二值化网络，这是非常不合适的。
我对于文章提出的结构有点质疑，这种结构可能只是凑巧的效果还不错，但是结构Improvement的结构太过于古怪。但是总体来说，这篇文章没有BDN那篇文章对于原理讲的那么清晰，应该按照BDN文章的思路走，去探索具有更好的效果的结构。
文中有一段证明了MeliusNet是特殊适应于BNN的结构，因为用模型大小相近的DenseNet和MeliusNet相比，两者的全精度浮点模型的识别精度几乎相近，但是若加入二值化处理，MeliusNet效果比DenseNet更好。但是事实上这种证明逻辑并不严谨，因为从网络模型大小来看，MeliusNet参数与操作都要比DenseNet大一些，而由于浮点网络的准确率已经很高了，往上进行一定的提升是非常难的，所以看起来是准确率相近。但由于BNN的模型精度较差，因此模型参数多带来的影响会比较明显，二值化的MeliusNet效果好也就在情理之中了，并不能证明出来它就是特殊的合适结构。

对于BN层的改造提出的一些想法

之前在8bit量化中采用BN融合的方法可以将卷积与BN融合在一起，减小了运算量。在现在这个结构中，都提倡先BN之后再进行二值化然后进行卷积，并且利用了同或与popcount代替了卷积提速，那么BN有没有一些可以提速的方法呢？
BN的公式如下$$Z=\gamma \frac{X-\mu }{\sqrt{{\sigma }^2+ϵ}}+\beta$$
在做完BN之后进行sign的二值化操作，因此事实上这个$Z$的值并不重要，我们要的只是他的符号。由于在前向传播的时候，除了$X$之外的参数都是训练好的定值，故判断$Z$的符号可以通过比较大小来判断，即比较$X$与$$\mu -\frac{\sqrt{{\sigma }^2+ϵ}\cdot \beta }{\gamma }$$的大小关系。注意：这里面$\gamma$的正负对于判断结果是有影响的，应分开讨论。
在具体的网络结构中，若$X$的值是之前经过Bconv得到的，则有一定是一个整数，在进行前向推理时，可以考虑将与之要比较的数近似为整数再进行比较，这样将浮点数的比较转化为整数的比较，还可以进一步的减少运算量。