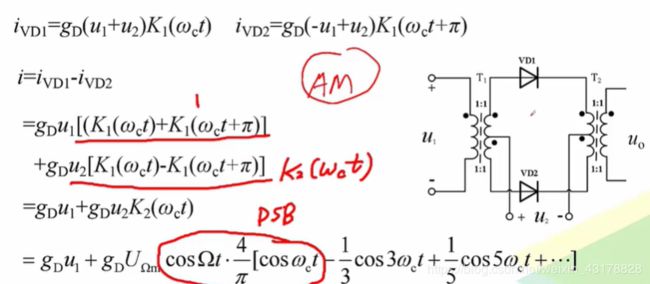通信电子电路（二十三）作业讲解 第四章

从题干强调调制系数，我们估计这个调制方式就是普通的AM，包含两个边带和载波carrier wave 因此
$$P=P_c+2P_{SB}=(1+\frac{m_a^2}{2})P_c$$
当调制系数$m_a=1$，$P_{SB}=\frac{1}{4}{m}_a^2{P}_c=250W$
∴ $P=P_c+2P_{SB}=1500W$

同理，当调制系数$m_a=0.7$，$P_{SB}=\frac{1}{4}{m}_a^2{P}_c=250W$
∴ $P=P_c+2P_{SB}=1245W$

题干翻译：

（1）AM信号频谱特点：中间是载波信号，${\omega }_c$，左右两个边带${\omega }_c-\Omega$以及${\omega }_c+\Omega$，其中$\Omega$是调制信号（源信号）,如图

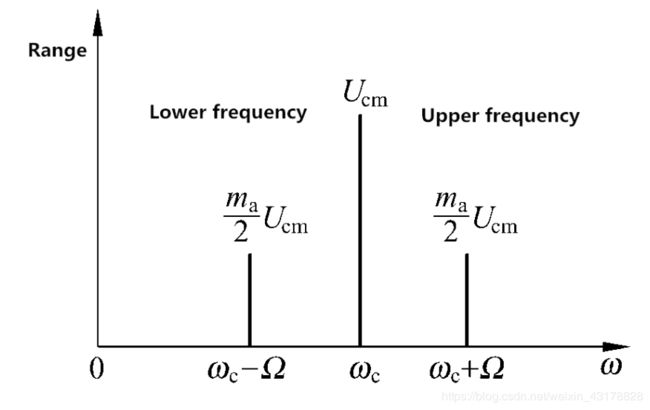
而DSB就是去掉了中间的载波频谱，只保留边带，降低总功率，如图：

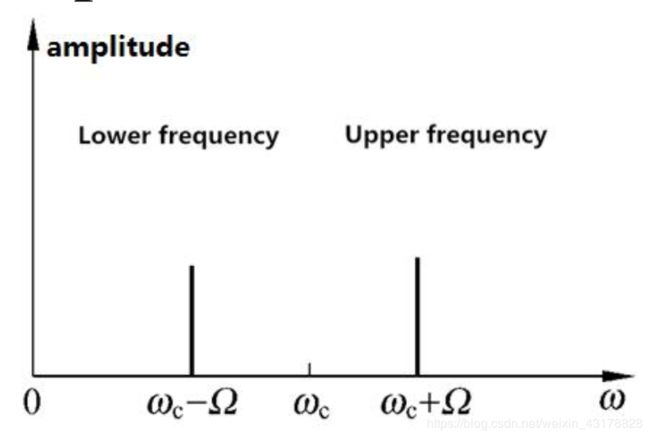
而SSB进一步利用边带对称，只保留一个边带，将功率降到最低

现在，我们很容易判断，$u_1$是普通的AM信号，而$u_2$是DSB-AM信号
我们利用积化和差可以处理一下：
$$u_1=2cos2000\pi t+0.3cos1800\pi t+0.3cos2200\pi t=2(1+0.3cos200\pi t)cos2000\pi t$$
由此可以提取出以下参数：

• $U_{cm}=2V$
• $m_a=0.3$
• $\Omega =200\pi$
• ${\omega }_c=2000\pi$

$u_2$呢？其实细心的你应该发现，$u_2$就是$u_1$去掉载波后的DSB-AM，那么之前提取的参数对这个DSB仍然有效 两者参数相同
（2）注意“unit resistor”，所以负载就是$1\Omega$，由
$$P=P_c+2P_{SB}$$
$$P_c=\frac{U_{cm}^2}{2R}=2W$$
$$P_{SB}=\frac{1}{4}{m}_a^2{P}_c=0.045W$$
可以得到：
$$P=2.09W$$
而$u_2$是$u_1$去掉载波的DSB-AM信号，因此总功率$P=2P_{SB}=0.09W$
可以看到，DSB相对于原始的AM做了多么有用的功率优化：）

（3）带宽我们用Hz为单位表示的话，$$B_{u1}=B_{u2}=\frac{2\Omega }{2\pi }=200Hz$$

题干翻译：

(1)C的范围应该满足两个因素：

• 检波效率${\eta }_d$越高越好
• 不发生失真

我们希望检波效率趋近于100% ，就要满足：
$$R_{L}C>>\frac{1}{f_c}$$
同时，我们要避免对角线失真：
$$C<\frac{\sqrt{1-m_a^2}}{m_a}\times \frac{1}{\Omega R_L}=0.15pF$$
∴$215pF<<C<<0.15\mu F$
另外，根据公式可得$$R_{in}=\frac{R_L}{2{\eta }_d}=5k\Omega$$
这里，我们设计的是让检波效率尽量趋近于100% 因此得到输入电阻为$5k\Omega$

(2) 同理，我们希望检波效率趋近于100% ，就要满足：$R_{L}C>>\frac{1}{f_c}$
同时，我们要避免对角线失真：$C<\frac{\sqrt{1-m_a^2}}{m_a}\times \frac{1}{\Omega R_L}=0.11nF$
∴$3.3pF<<C<<0.11nF$
另外，根据公式可得$R_{in}=\frac{R_L}{2{\eta }_d}=5k\Omega$，${\eta }_d\to 100$， 因此得到输入电阻为$5k\Omega$

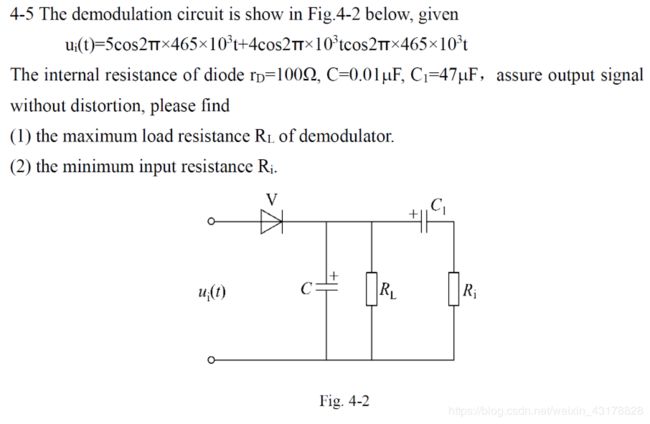
（1）因为放电速度太慢导致的对角线失真，我们可以避免，由
$$R_L<\frac{\sqrt{1-m_a^2}}{m_a}\times \frac{1}{\Omega C}=11.9K\Omega$$

(2)为了避免割底失真，有：
$$m_a\le \frac{R_i}{R_i+R_L}\to R_i\ge 47.6K\Omega$$

为了避免在混频器应用中的副波道干扰，由
$$f_M=\frac{p}{q}{f}_L\pm \frac{1}{q}{f}_I\to f_c=\frac{q}{p}{f}_M-\frac{p\pm 1}{p}{f}_I$$
我们取以下几种情况来分析：
当$p=1,q=1,f_{c1}=700kHz,f_{c2}不在接受范围之内$

当$p=1,q=0,f_{c1},f_{c2}都不在接受范围之内$

当$p=1,q=2,f_{c1}=1400kHz,f_{c2}不在接受范围之内$

当$p=1,q=3,f_{c1}=1170kHz,f_{c2}不在接受范围之内$

综上所述，在$f_{c1}=1170kHz$出现了4阶副波段干扰，在$f_{c1}=1400kHz$出现了3阶副波段干扰

其他习题