二叉树
继续听课5555
操作集:
1、Boolean IsEmpty( BinTree BT ): 判别BT是否为空;
2、void Traversal( BinTree BT ):遍历,按某顺序访问每个结点;
3、BinTree CreatBinTree( ):创建一个二叉树。
常用的遍历方法有:
void PreOrderTraversal( BinTree BT ):先序----根、左子树、右子树;
void InOrderTraversal( BinTree BT ): 中序—左子树、根、右子树;
void PostOrderTraversal( BinTree BT ):后序—左子树、右子树、根
void LevelOrderTraversal( BinTree BT ):层次遍历,从上到下、从左到右
1.二叉树的储存结构
(1)顺序储存
完全二叉树用数组储存较为方便,按从上至下、从左到右顺序存储
n个结点的完全二叉树的结点父子关系:
···非根结点(序号 i > 1)的父结点的序号是[i / 2];
···结点(序号为 i )的左孩子结点的序号是 2i,(若2i > n,没有左孩子);
···结点(序号为 i )的右孩子结点的序号是 2i+1,(若2i +1>n,没有右孩子);
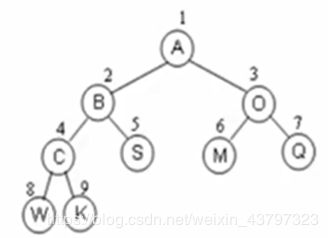

若将一般的二叉树补齐成完全二叉树放进数组,对应关系依然存在,但会造成空间浪费
2.链式储存
typedef struct TreeNode *BinTree; //结构指针
typedef BinTree Position;
struct TreeNode{
ElementType Data;
BinTree Left;
BinTree Right;
}
Left Data Right
data
Left Right
(1)先序遍历:
void PreOrderTraversal( BinTree BT ) {
if( BT ) {
printf(“%d”, BT->Data);
PreOrderTraversal( BT->Left );
PreOrderTraversal( BT->Right ); }
}
(2)中序遍历:
void InOrderTraversal( BinTree BT ) {
if( BT ) {
InOrderTraversal( BT->Left );
printf(“%d”, BT->Data);
InOrderTraversal( BT->Right ); }
}
(3)后序遍历
void PostOrderTraversal( BinTree BT ) {
if( BT ) {
PostOrderTraversal( BT->Left );
PostOrderTraversal( BT->Right);
printf(“%d”, BT->Data);
}
}
先序、中序和后序遍历过程:遍历过程中经过结点的路线一
样,只是访问各结点的时机不同。
图中在从入口到出口的曲线上用×、星星和三角形三种符号分别标
记出了先序、中序和后序访问各结点的时刻
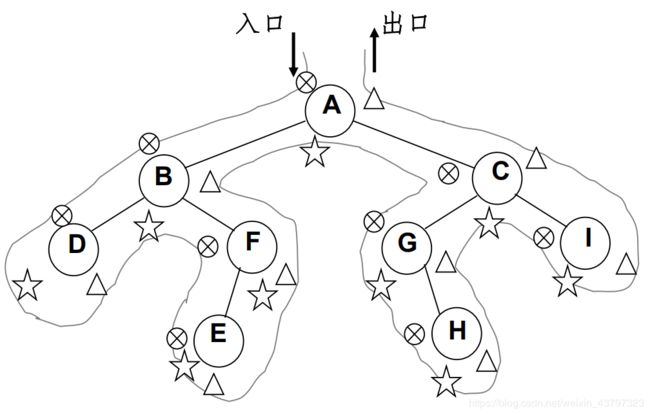 连线表示访问的顺序:每个结点会被经历三次,如图中的D结点,是连着被碰到的
连线表示访问的顺序:每个结点会被经历三次,如图中的D结点,是连着被碰到的
(4)二叉树的非递归遍历:使用堆栈
···中序遍历非递归遍历算法:
遇到一个结点,就把它压栈,并去遍历它的左子树;
当左子树遍历结束后,从栈顶弹出这个结点并访问它;
然后按其右指针再去中序遍历该结点的右子树。
void InOrderTraversal( BinTree BT ) { BinTree T=BT;
Stack S = CreatStack( MaxSize ); /*创建并初始化堆栈S*/
while( T || !IsEmpty(S) ){ //树不空和堆栈不空
while(T){ /*一直向左并将沿途结点压入堆栈*/
Push(S,T); //把根结点T压入堆栈,是第一次碰到它
T = T->Left; }
if(!IsEmpty(S)){
T = Pop(S); /*结点弹出堆栈*/ //之后就转向右子树,所以是第二次碰到它
printf(“%5d”, T->Data); /*(访问)打印结点*/
T = T->Right; /*转向右子树*/ // T变成了右子树的根结点
}
}
}
···先序遍历的非递归:
???
啦啦啦啦啦
···后序遍历的非递归:
后序遍历需要访问左子树->右子树->根 ,所以要Pop某个根结点的条件是右结点已经被Pop或者右结点为NULL,如果不满足条件,则说明右侧结点还未被Pop(PrePop变量记录上一个Pop的结点,并用于判断是不是当前结点的右结点)后序遍历的Pop过程可以是连续的,直到有不满足条件的结点出现才停止Pop过程,所以写成循环
void PostOrderTraversal(BinTree BT) {
BinTree T = BT, PrePop = NULL; //PrePop记录上一个Pop出来的结点
Stack S = CreatStack(MaxSize);
while ((T || !IsEmpty(S))&&PrePop!=BT) { //若PrePop的是根结点,则后序遍历结束,退出外层循环
while (T) { //一直向左将结点压入堆栈
Push(S, T);
T = T->Left; } //将Pop的过程改为循环
while (!IsEmpty(S)) { //后序遍历有两种情况可以Pop该结点
T = Pop(S);
if (T->Right == PrePop || T->Right == NULL) { //该结点的右结点为空或者上一次Pop的是该结点的右结点
printf("%05d", T->Data);
PrePop = T;
}
else { //若不满足以上两种情况 说明该节点右侧节点还未被Pop
Push(S, T); //则将该结点重新压回堆栈
T = T->Right; //然后指向该结点的右节点
break; //退出Pop循环 } }
}
}
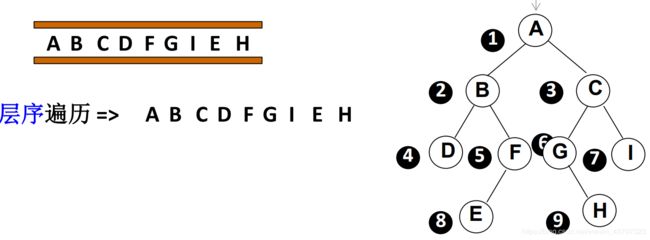
(5)层序遍历:
只能通过结点访问左儿子,访问左儿子之后要想访问右儿子,必须在这之前把右儿子或者父结点储存起来,所以需要一个储存结构保存暂时不访问的结点,可以用堆栈(保存父结点)、队列(保存右儿子)
···队列:
根结点入队,开始执行循环:
从队列中取出一个元素;
访问该元素所指结点;
若该元素所指结点的左、右孩子结点非空,则将其左、右孩子的指针顺序入队。
void LevelOrderTraversal ( BinTree BT ) {
Queue Q; BinTree T;
if ( !BT ) return; /* 若是空树则直接返回 */
Q = CreatQueue( MaxSize ); /*创建并初始化队列Q*/
AddQ( Q, BT );
while ( !IsEmptyQ( Q ) ) {
T = DeleteQ( Q );
printf(“%d\n”, T->Data); /*访问取出队列的结点*/
if ( T->Left ) AddQ( Q, T->Left );
if ( T->Right ) AddQ( Q, T->Right ); } }
···将层序遍历中的队列改为堆栈:讨论班看到的最佳回复,然而我看不懂
层序遍历与其他三种(前序、中序和后序遍历)的主要区别是:层次遍历通过各结点一次性获得其左右儿子结点信息并借助队列以自顶向下的顺序,形成按宽度优先方式遍历二叉树。而其他三种遍历均是各结点借助堆栈的逆序特点,按自底向上的顺序逐步处理左右儿子,形成按深度优先方式遍历二叉树。
如果将层序遍历程序中的队列直接改为堆栈,同时将入栈(原来是入队)顺序改为先右儿子再左儿子,其遍历输出结果就是前序遍历。
对于中序遍历和后序遍历,关键是要判别左子树和右子树什么时候遍历结束。如果将层序遍历程序中的队列改为堆栈,同时仍然按照层次遍历的整体控制思路,对出入栈操作做些修改,仍然可以实现中序遍历和后序遍历。要点是:在原来程序控制过程中,结点出队后是将其左右儿子入队;现在可将控制过程改为:结点出栈后,将当前结点“加塞”在其左右儿子中再次入栈。如果“加塞”在左右儿子之间再次入栈就是中序遍历,如果“加塞”在左右儿子之前再次入栈就是后序遍历。也就是每个结点做两次出入栈处理(类似后序遍历的非递归程序):
中序遍历要点:结点出栈时,如果是第一次出栈,按照右儿子、当前结点、左儿子顺序入栈,即左儿子在栈顶,当前结点此时是第二次入栈。将来如果第二次出栈则直接输出。
后序遍历要点:过程与上述中序遍历一样,唯一区别是入栈顺序为:当前结点、右儿子、左儿子。
