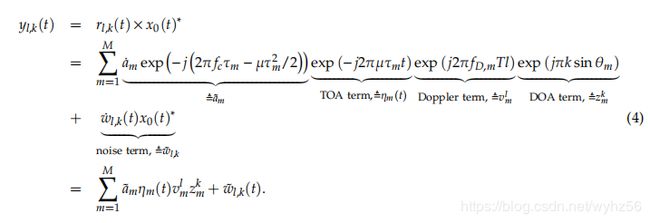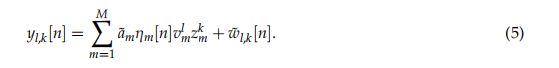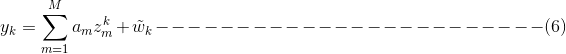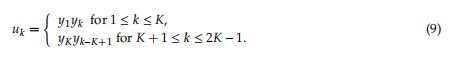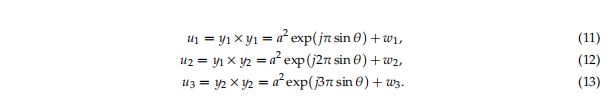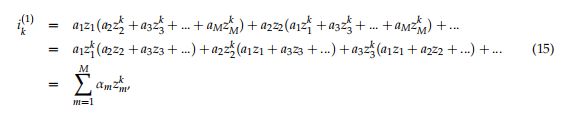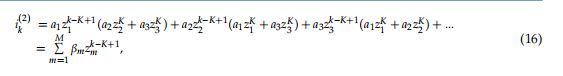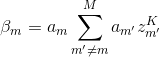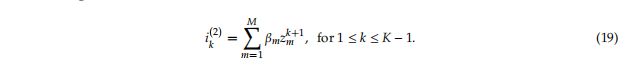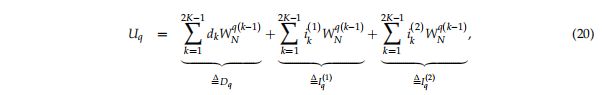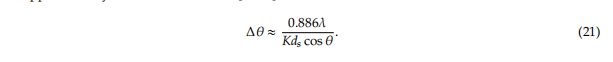A Novel DFT-Based DOA Estimation by a Virtual Array Extension Using Simple Multiplications for FMCW

FMCW雷达：基于DFT的DOA估计 （使用基于简单乘法的虚拟阵列扩展）

本文仅为翻译手册，留以自己查看，若需要深入交流，可以在个人分类中查找解析与实践内容（可能未发布），或与作者联系 

摘要

我们提出了一种新的基于离散傅里叶变换（DFT）的方向（DOA）估计（Direction of arrival），其通过虚拟阵列扩展使用简单的乘法用于调频连续波（FMCW）雷达。基于DFT的DOA估计通常用于雷达系统，因为它为实时信号处理提供了低复杂度的优点。为了增强DOA估计的分辨率或减少丢失的检测概率，必须具有相当数量的信道信号。然而，由于空间和成本的限制，增加信道信号的数量并不容易。为了解决这个问题，我们通过使用给定信道信号的简单乘法产生虚拟信道信号来增加有效信道信号的数量。信道信号的增加允许所提出的方案在使用相同数量的信道信号时比传统方案更准确地检测DOA。仿真结果表明，与传统的基于DFT的方法相比，该方案实现了改进的DOA估计。此外，通过实验验证了所提方案在实际环境中的有效性。

Introduction

最近，对调频连续波（FMCW）雷达系统进行了多项研究，因为它具有许多优点，包括成本和复杂度低于等效脉冲雷达系统[1-4]。在FMCW雷达系统中，估计到达方向（DOA）是一个主要的研究问题。在DOA估计中，通常采用基于离散傅立叶变换（DFT）的DOA估计或所谓的“DBF（数字波束成形）”[1];与超分辨率算法相比，该方法具有实时信号处理的低复杂度的优点，例如多信号分类器（MUSIC）和通过旋转不变技术（ESPRIT）估计信号参数，其具有非常高的复杂度[5]-7]。基于DFT的DOA估计的主要挑战之一是增强DOA估计的分辨率，同时降低丢失的检测概率[1,8]。为了实现这些目标，必须拥有大量的信道信号。然而，在实践中，由于空间和成本的限制，很难增加信道信号的数量。

较早的DOA估计方法又称为波束形成方法，而该波束形成方法利用了空域维纳滤波的匹配概念，由阵列流形在信号空间中的投影大小判定信号方向，后来随着研究的深入，高分辨谱估计技术的发展，才把DOA估计和波束形成加以区分，DOA估计是为了确定信号的方位，从接收数据中测出信号方向，不管信号是有用信号还是干扰信号，在DOA估计方向图中都表现为峰值，而此峰值并不是实际阵列输出功率；波束形成是传统滤波的空域拓展，其根本目的是有效提取有用信号并抑制噪声和干扰，在方向图中表现为有用信号方向形成峰值、干扰方向形成零陷，可以认为DOA估计为波束形成的前端处理，确定期望信号和干扰方向后，阵列对期望信号方向形成波束并在干扰方向形成零陷。

作为解决方案，虚拟阵列（VA）方法已被提出[9-12]。通过使用数学操作或多个频带，这些方法尝试使用现有信道信号来增加DOA估计的分辨率。在[9,10]中，通过使用信道信号的共轭对应物，形成VA以扩展等效阵列孔径，使得它可以处理比给定信道信号更多的源。为了即使在共轭操作之后也保持相位信息，假设非圆形信号，例如二进制相移键控（BPSK）调制信号。然而，如[11]中所述，假设非圆形信号是不实际的。这是因为，即使源是非圆形的，由于相移，接收信号也不是实值的，而是复值的，对于每个信号可以是不同的。同时，在[12]中，作者试图通过使用多个频带来提高分辨率，即他们利用根据频带的相移差异。然而，在实践中，由于多个射频（RF）设备的高成本，使用多个频带并不容易。同时，为了提高分辨率，已经提出了使用多输入多输出（MIMO）天线系统的DOA估计算法[13,14]。在没有大幅增加系统的物理尺寸的情况下，这些算法可以通过虚拟地增加信道信号来改善DOA分辨率。然而，这些算法不仅需要额外的发射天线，而且还需要诸如发射信号之间的正交性的时间和频率的附加资源。

在本文中，我们提出了一种新的基于DFT的DOA估计方法，该方法利用在[15,16]中假设正弦信号的情况下使用给定信号进行外推检测点是可能的。
为了增加信道信号的数量，通过使用给定信道信号的乘法产生虚拟信道信号，而不假设非圆形信号和使用附加发射天线。以这种方式，与传统的基于DFT的DOA估计方案相比，所提出的方案显着地降低了丢失检测和均方根误差（RMSE）的概率，同时使用相同数量的信道信号。尽管性能得到改善，但所提出的方案的计算复杂度几乎与传统的基于DFT的DOA估计方案的计算复杂度相同。当存在多个目标时，由于在虚拟信道信号的产生期间的乘法的交叉项，不可避免地发生干扰项。我们研究了这些干扰项对整体性能的影响。
仿真结果表明，与传统方案相比，该方案实现了较低的RMSE和较低的检测丢失概率。此外，通过在实际环境中的实验验证了所提出的方案的有效性。

Signal Model and Notation

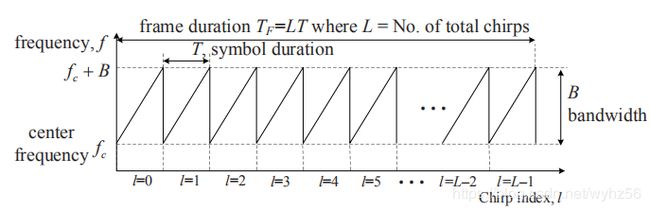
如图1所示，由总共L个chirps组成的发射（TX）FMCW信号帧用x（t）表示，并表示为

其中是归一化矩形信号，是FMCW线性调频信号的持续时间。
FMCW chirps信号表示如下： 

其中是载波频率，是chirp信号的瞬时频率的变化率。

图1. FMCW雷达的发射（TX）信号的结构，其中f是频率，B是带宽，L是每帧的chirp数，T是符号持续时间，是中心频率，是帧持续时间。

我们考虑M个远场，非相干，窄带目标撞击具有K个元素的均匀线性阵列（ULA）。用于第l个chirp的第k个数组元素的接收（RX）信号由r1，k（t）表示，并表示为[2]：

其中是第m个目标的复振幅，是相邻元素之间的间距，是载波频率的波长，，和分别是是往返时间延迟，因为目标运动导致的多普勒频率和第m个目标的DOA角度; 是第k个阵列和第l个chirp的附加型高斯白噪声（AWGN）信号。
通过将共轭FMCW TX信号乘以并假设，第l个线性调频和第k个阵列的差拍信号表示为如下

可表示为到达时间（TOA），多普勒和DOA部分的乘积：

在的模数转换（ADC）之后，具有采样频率的等式（4）的离散时间模型由表示.对于n = 0,1，...，，即，其中是采样间隔，即 ，是样本数，即，因此，等式（4）被重写为：

DFT-Based DOA Estimation in FMCW Radar Systems

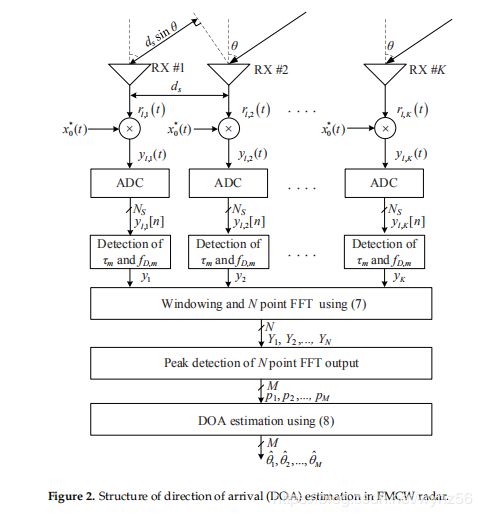
本节讨论FMCW雷达系统中基于DFT的DOA估计。图2显示了FMCW雷达系统的DOA估计的流程。如图2所示，首先，使用2D DFT估计用于估计目标范围的TOA项和用于估计目标速度的多普勒项[4]。然而，TOA和多普勒项的估计不是本文中的主要问题，因此我们省略了对它们的详细描述。为了集中于DOA估计，和TOA和多普勒项的乘积表示为新变量，即。另外，通过省略样本索引n和chirp索引l，等式（4）简单地表示如下：

为了从等式（6）估计DOA信息，执行DBF的DFT，即，对于1≤k≤K[8]，在上执行DFT操作。的第q个DFT输出由表示，并获得如下：      

其中是N点DFT算子，即。然后，执行峰值检测处理，为峰值索引，最后，估计的第m个DOA项θm估计如下：

Proposed Algorithm

本节说明了所提出的基于DFT的DOA估计。所提出的方案的关键思想是通过使用给定的实信道信号的乘法来扩展信道信号的有效数量。首先，我们解决了所提算法的结构。然后，我们研究了当存在多个目标时由于乘法而产生的干扰项所造成的影响;我们证明了所提出的方案提高了DOA分辨率。

Structure of the Proposed Algorithm

在本节中，我们将说明所提算法的结构。所提出的算法通过在等式（6）中的给定两个间隔实信道（差拍）信号之间的乘法新生成第k个信道信号，如下：

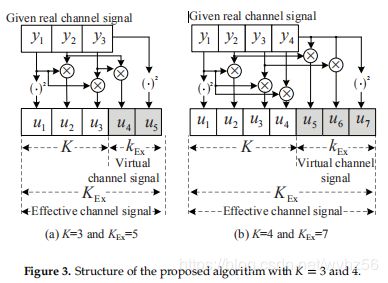
图3示出了所提出的方案的结构，其中K = 3和K = 4。
在图3中，表示虚拟信道信号的数量，是有效信道信号的数量，即。也就是说，可以最大设置为，最大可以设置为.在图3a，b中，可以看到分别另外生成两个和三个虚拟通道信号（阴影部分）。

为了研究所提算法的特征，让我们观察一个通过乘以和得到的新的虚拟信号，其中等于，1≤k≤K，等于，K +1≤k≤2K-1.因此，新生成的信道信号uk表示为：

其中是期望的项，其包括每个目标的DOA信息，是由于多个信号之间的乘法而产生的干扰项，并且是噪声项。
同时，的统计数据与乘法前的情况相同。这是因为两个噪声项是每个噪声分量的线性组合，因此两个噪声项仍然保持高斯分布。另外，由于复高斯随机变量的乘法分布是高斯分布，第三项也遵循复杂的高斯分布[17]。因此，噪声项可以表示为一个变量，即wk，如等式（10）所示。
为了便于理解，我们在K = 2和M = 1的情况下示出了一个例子。通过使用等式（9），获得如下的，和：

根据等式（11） - （13），不仅幅度项被保持为，而且θ的常量根据阵列索引k而增加。这意味着具有DOA信息的附加信道信号实际上由所提出的算法生成。

为了估计等式（10）中的DOA信息，DBF的DFT操作在上执行，如上一节所示。因此，第q个DFT输出由表示，并获得如下：

其中是N点DFT算子。然后，如图2所示，在所提出的方案中进行峰值检测处理。因此，M个指数对应于M个峰值。最后，根据获得的M指数估计DOA项。

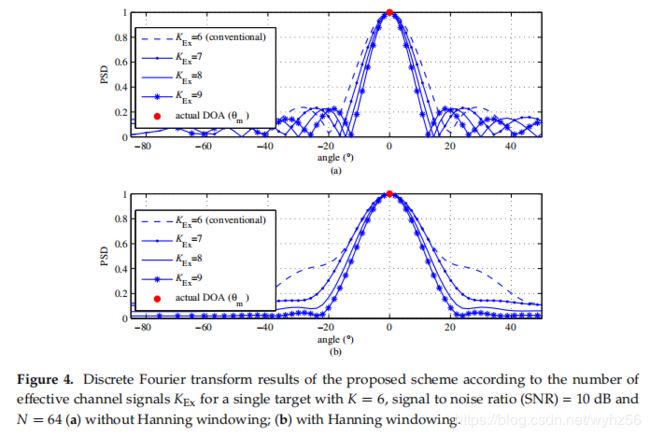
为了有效地显示所提出的方案的可行性，图4显示了| Uq | 通过所提出的方案获得了对于单个目标条件具有信噪比（SNR）= 10dB，N = 64和K = 6的几个。对于单个目标条件，没有干扰项，即等式（10）中的 = 0，因此仅存在期望项和噪声项。
在图4中，可以看出，随着的增加，用于估计DOA项的DFT输出的幅度变得更加清晰。这是因为信道信号的数量实际上从K增加到，如等式（9）和（14）所示。
同时，如等式（10）所示，干扰项在多个目标环境中共存，但是我们将在下一部分中说明干扰的影响是无关紧要的。
因此，从图4所示的结果可以推测，所提出的方案将比传统的基于DOA-DFT的估计方案实现更好的DOA估计。图4b示出了所提出的具有汉宁窗口的算法的DFT结果，以减轻旁瓣的影响。与图4a相比，DFT结果的宽度变宽，但由于Hanning窗口化，旁瓣的效果显着降低。

Analysis of Interference Signal Due to Cross Terms

该部分提供干扰信号的分析，其不可避免地通过等式（10）中的乘法产生。众所周知，DFT是线性操作。因此，我们可以只关注干扰项。根据等式（9），第一部分的，1≤k≤K由表示，并表示如下：

其中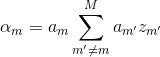。使用类似于等式（15）的表达式，第二部分的由表示并表示如下：

其中。因此，和通常表示为：

为了更直观地理解，以类似于的形式被重写，其方式如下：

从等式（17）和等式（19），示出了和分别包含DOA项和。
比较等式（10）中的和等式（17）中的以及等式（19）中的，和和具有不同幅度下的相同的DOA信息 。
众所周知，DFT是线性算子，因此意味着和对整体性能无关紧要。
为了证实我们假设干扰成分不会对整体性能产生重大影响，我们分析了的DFT输出。
通过使用DFT的线性度，等式（14）中的Uq可以表示为由，和表示的期望和干扰项的总和，如下：

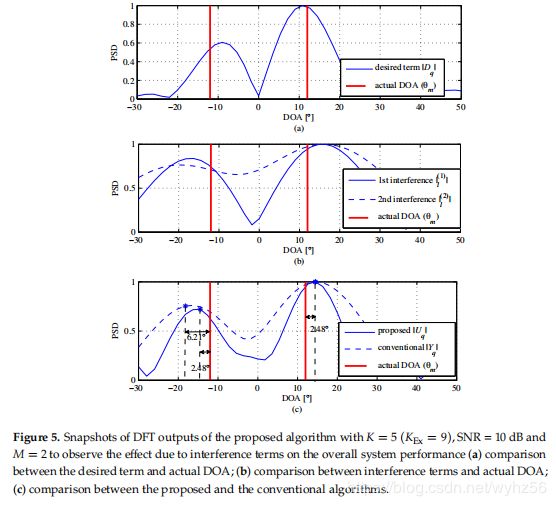
为简单起见，省略了噪声项。图5提供了DFT输出的归一化幅度的快照，其中K = 5，SNR = 10dB，= 9且M = 2.在图5a中，示出了扩展的期望信号Dq的结果。扩展的期望信号Dq不仅包括噪声项，还包括干扰项。| Dq |的峰值几乎完全遵循实际的DOA条款。图5b显示了和的结果。从图5b可以看出，它不像| |那么多，但是两个干扰项的峰值遵循实际DOA项并且与预期一致。图5c显示了的结果;的峰值也遵循实际的DOA项，即使包括干扰项以及与传统算法相比的噪声项。也就是说，所提出的算法的估计误差约为2.48°，这比传统算法的估计误差6.21°小，如图5c所示。这意味着干扰信号对整体性能无关紧要。

在图6中，示出了所提出的和传统算法的DFT输出的结果，以便比较在M = 2的情况下两种算法之间的分辨率性能。图6示出了所提出的算法区分两个不同的DOA项。另一方面，在传统算法中，两个目标被合并为一致，因此好像显示存在单个目标。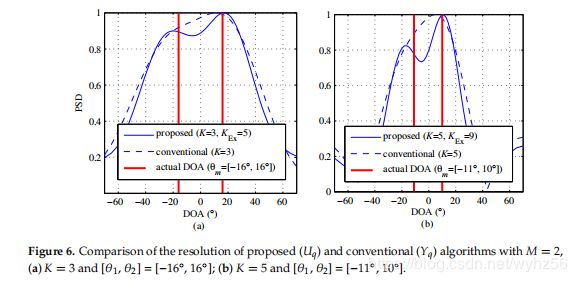

Simulation Results

在本节中，我们提供模拟结果来评估所提出方案的性能。将所提出的方案的结果与基于等式（6）的传统方案的结果进行比较。通常，我们设置和，并且等式（4）中的复振幅是随机且独立地生成的，具有均匀分布，即，的大小是,角度是。DFT N的大小设置为64.我们提出了平均超过个估计的蒙特卡罗模拟结果。为了有效地比较所提出的方案和传统方案的性能，我们采用两个指标，即均方根误差（RMSE）和丢失检测的概率，由表示。RMSE定义为，表示通过DFT输出的峰值检测获得的峰值数量将小于目标数量的概率。如果通过峰值检测发现的峰值数量低于目标数量M，则我们不在RMSE评估中包括这种情况。同时，通过考虑给定条件下的角分辨率Δθ来设定目标之间的角度差。角分辨率Δθ近似计算如下[18,19]：

图7示出了使用等式（21）根据K和角度的Δθ。随着K增加并且θ接近零，角度分辨率Δθ变小。在执行模拟时，将使用角度分辨率的信息。

图8示出了对于具有M = 2（θ1= 10°，θ2= 11°）的几个Ks，根据SNR的RMSE和Pmiss的提出的和传统的算法之间的比较。在所提出的算法中，KEx设定为2K K 1.设定两个角度θ1和θ2，使得|θ11θ2|。通过考虑K = 5处的角度分辨率Δθ= 21°。从图8a，b，提出的和传统的方案的RMSE和Pmiss通常随着K和SNR的增加而减小。然而，更密切地观察，对于所有K值和所有SNR区域，所提出的方案实现比传统方案更低的RMSE和更低的Pmiss。

未完成